Aunque los métodos de la sección anterior son útiles para describir y mostrar datos de la muestra, el verdadero poder de la estadística se revela cuando utilizamos las muestras para darnos información sobre las poblaciones. En este contexto, una población es toda la colección de objetos de interés, por ejemplo, los precios de venta de todas las viviendas unifamiliares en el mercado de la vivienda representado por nuestro conjunto de datos. Nos gustaría saber más sobre esta población para ayudarnos a tomar una decisión sobre qué casa comprar, pero los únicos datos que tenemos son una muestra aleatoria de 30 precios de venta.
Sin embargo, podemos emplear el «pensamiento estadístico» para hacer inferencias sobre la población de interés analizando los datos de la muestra. En concreto, utilizamos la noción de modelo -una abstracción matemática del mundo real- que ajustamos a los datos de la muestra. Si este modelo se ajusta razonablemente a los datos, es decir, si puede aproximarse a la forma en que varían los datos, suponemos que también puede aproximarse al comportamiento de la población. El modelo proporciona entonces la base para tomar decisiones sobre la población, por ejemplo, identificando patrones, explicando la variación y prediciendo valores futuros. Por supuesto, este proceso sólo puede funcionar si los datos de la muestra pueden considerarse representativos de la población.
A veces, incluso cuando sabemos que una muestra no ha sido seleccionada al azar, podemos modelarla. Entonces, puede que no seamos capaces de inferir formalmente sobre una población a partir de la muestra, pero todavía podemos modelar la estructura subyacente de la muestra. Un ejemplo sería una muestra de conveniencia: una muestra seleccionada más por razones de conveniencia que por sus propiedades estadísticas. Al modelar este tipo de muestras, los resultados deben ser comunicados con la precaución de restringir las conclusiones a objetos similares a los de la muestra. Otro tipo de ejemplo es cuando la muestra comprende toda la población. Por ejemplo, podríamos modelar los datos de los 50 estados de los Estados Unidos de América para entender mejor cualquier patrón o asociación sistemática entre los estados.
Dado que el mundo real puede ser extremadamente complicado (en la forma en que los valores de los datos varían o interactúan juntos), los modelos son útiles porque simplifican los problemas para que podamos entenderlos mejor (y entonces tomar decisiones más eficaces). Por tanto, por un lado, necesitamos que los modelos sean lo suficientemente sencillos como para poder utilizarlos fácilmente para tomar decisiones, pero por otro lado, necesitamos modelos que sean lo suficientemente flexibles como para proporcionar buenas aproximaciones a situaciones complejas. Afortunadamente, a lo largo de los años se han desarrollado muchos modelos estadísticos que proporcionan un equilibrio eficaz entre estos dos criterios. Uno de estos modelos, que proporciona un buen punto de partida para los modelos más complicados que consideraremos más adelante, es la distribución normal.
Desde una perspectiva estadística, una distribución de probabilidad es un modelo teórico que describe cómo varía una variable aleatoria. Para nuestros propósitos, una variable aleatoria representa los valores de los datos de interés en la población, por ejemplo, los precios de venta de todas las viviendas unifamiliares en nuestro mercado inmobiliario. Una forma de representar la distribución poblacional de los valores de los datos es en un histograma, como se describe en el apartado 1.1. La diferencia ahora es que el histograma muestra toda la población en lugar de sólo la muestra. Dado que la población es mucho más grande que la muestra, los intervalos del histograma (los rangos consecutivos de los datos que comprenden los intervalos horizontales para las barras) pueden ser mucho más pequeños, por ejemplo, lo siguiente muestra un histograma para una población simulada de 1.000 precios de venta.
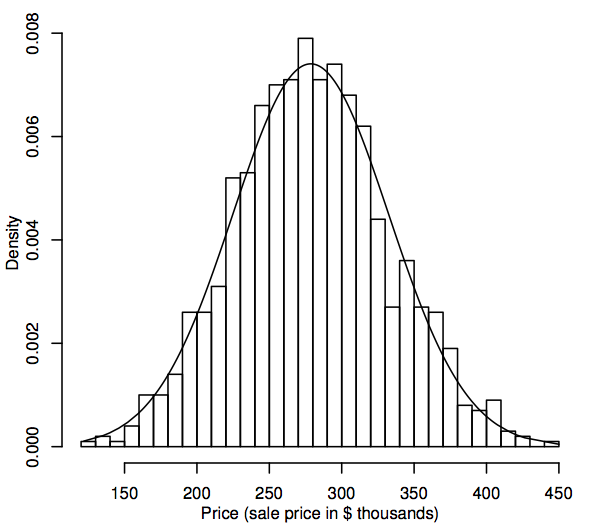
A medida que el tamaño de la población aumenta, podemos imaginar que las barras del histograma se vuelven más delgadas y más numerosas, hasta que el histograma se asemeja a una curva suave en lugar de una serie de pasos. Esta curva suave se denomina curva de densidad y puede considerarse como la versión teórica del histograma de la población. Las curvas de densidad también permiten visualizar distribuciones de probabilidad como la normal. Una curva de densidad normal se superpone al histograma anterior. El histograma de la población simulada sigue la curva muy de cerca, lo que sugiere que esta distribución de la población simulada se aproxima bastante a la normalidad.
Para ver cómo una distribución teórica puede resultar útil para hacer inferencias estadísticas sobre poblaciones como la de nuestro ejemplo de los precios de la vivienda, tenemos que examinar más de cerca la distribución normal. Para empezar, consideraremos una versión particular de la distribución normal, la normal estándar, representada por la siguiente curva de densidad.
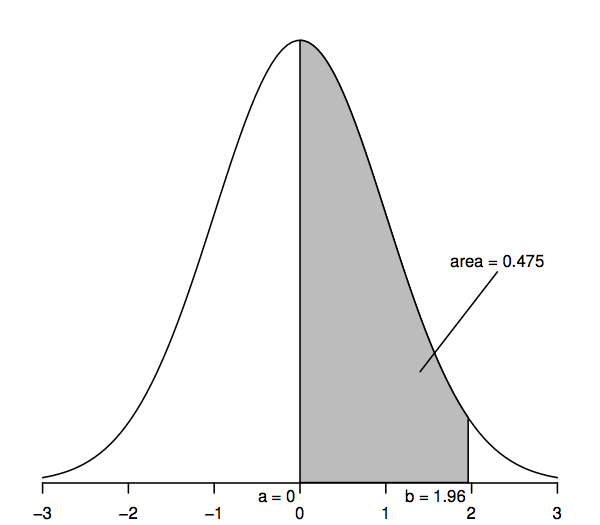
Las variables aleatorias que siguen una distribución normal estándar tienen una media de 0 (por lo que la curva es simétrica en torno a 0, que está bajo el punto más alto de la curva) y una desviación estándar de 1 (por lo que la curva tiene un punto de inflexión -donde la curva se curva primero en un sentido y luego en el otro- en +1 y -1). La curva de densidad normal se denomina a veces «curva de campana», ya que su forma se asemeja a la de una campana.
La característica clave de la curva de densidad normal que nos permite hacer inferencias estadísticas es que las áreas bajo la curva representan probabilidades. Toda el área bajo la curva es uno, mientras que el área bajo la curva entre un punto del eje horizontal (a, por ejemplo) y otro punto (b, por ejemplo) representa la probabilidad de que una variable aleatoria que sigue una distribución normal estándar se encuentre entre a y b. Así, por ejemplo, la figura anterior muestra que la probabilidad es 0.475 de que una variable aleatoria normal estándar se encuentre entre a=0 y b=1,96, ya que el área bajo la curva entre a=0 y b=1,96 es 0,475.
Podemos obtener los valores de estas áreas o probabilidades de diversas fuentes: tablas de números, calculadoras, hojas de cálculo o software estadístico, sitios web, etc. A continuación imprimimos sólo algunos valores seleccionados, ya que la mayoría de los cálculos posteriores utilizan una generalización de la distribución normal llamada «distribución t». Además, en lugar de áreas como la sombreada en la figura anterior, será más útil considerar las «áreas de cola» (por ejemplo a la derecha del punto b), por lo que, en aras de la coherencia con las tablas de números posteriores, la siguiente tabla permite calcular dichas áreas de cola:
En particular, el área de la cola superior a la derecha de 1,96 es 0,025; esto equivale a decir que el área entre 0 y 1,96 es 0,475 (ya que toda el área bajo la curva es 1 y el área a la derecha de 0 es 0,5). Del mismo modo, el área de dos colas, que es la suma de las áreas a la derecha de 1,96 y a la izquierda de -1,96, es dos veces 0,025, es decir, 0,05.
¿Cómo nos ayuda todo esto a hacer inferencias estadísticas sobre poblaciones como la de nuestro ejemplo de los precios de la vivienda? La idea esencial es que ajustamos un modelo de distribución normal a nuestros datos de la muestra y luego utilizamos este modelo para hacer inferencias sobre la población correspondiente. Por ejemplo, podemos utilizar cálculos de probabilidad para una distribución normal (como se muestra en la figura anterior) para hacer afirmaciones de probabilidad sobre una población modelada utilizando esa distribución normal; mostraremos exactamente cómo hacerlo en la sección 1.3. Sin embargo, antes de hacerlo, haremos una pausa para considerar un aspecto de esta secuencia inferencial que puede hacer que el proceso se realice o se rompa. ¿Proporciona el modelo una aproximación lo suficientemente cercana al patrón de valores de la muestra como para que podamos confiar en que el modelo representa adecuadamente los valores de la población? Cuanto mejor sea la aproximación, más fiables serán nuestras afirmaciones inferenciales.
Hemos visto antes cómo una curva de densidad puede considerarse un histograma con un tamaño de muestra muy grande. Así que una forma de evaluar si nuestra población sigue un modelo de distribución normal es construir un histograma a partir de los datos de nuestra muestra y determinar visualmente si «parece normal», es decir, aproximadamente simétrico y con forma de campana. Se trata de una decisión un tanto subjetiva, pero con la experiencia se debería descubrir que resulta más fácil discernir los histogramas claramente no normales de los que son razonablemente normales. Por ejemplo, mientras que el histograma anterior parece claramente una curva de densidad normal, la normalidad del histograma de 30 precios de venta de muestra del apartado 1.1 es menos segura. Una conclusión razonable en este caso sería que, aunque este histograma de muestra no es perfectamente simétrico ni tiene forma de campana, se aproxima lo suficiente como para que el correspondiente histograma (hipotético) de la población pueda ser normal.
Una forma alternativa de evaluar la normalidad es construir un diagrama QQ (diagrama cuantil-cuantil), también conocido como diagrama de probabilidad normal, como se muestra aquí para los datos de los precios de la vivienda:
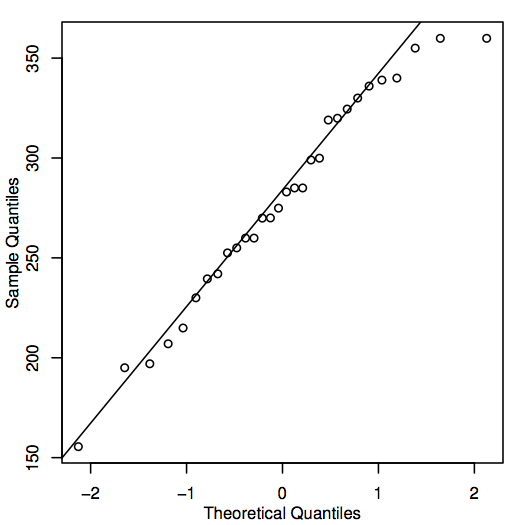
Si los puntos del diagrama QQ se encuentran cerca de la línea diagonal, entonces los valores poblacionales correspondientes podrían ser normales. Si los puntos se encuentran generalmente lejos de la línea, entonces la normalidad está en duda. De nuevo, se trata de una decisión algo subjetiva que resulta más fácil de tomar con la experiencia. En este caso, dado el tamaño bastante pequeño de la muestra, los puntos están probablemente lo suficientemente cerca de la línea que es razonable concluir que los valores de la población podrían ser normales.
También hay una variedad de métodos cuantitativos para evaluar la normalidad-véase la Sección 6.3.