Ačkoli metody uvedené v předchozí části jsou užitečné pro popis a zobrazení výběrových dat, skutečná síla statistiky se projeví, když použijeme výběry k získání informací o populacích. V tomto kontextu je populací celý soubor objektů zájmu, například prodejní ceny všech rodinných domů na trhu s bydlením reprezentované naším souborem dat. Rádi bychom se o této populaci dozvěděli více informací, které by nám pomohly při rozhodování o tom, který dům koupit, ale jedinými údaji, které máme k dispozici, je náhodný vzorek 30 prodejních cen.
Přesto můžeme použít „statistické myšlení“ a na základě analýzy údajů ze vzorku vyvodit závěry o populaci, která nás zajímá. Použijeme zejména pojem modelu – matematické abstrakce reálného světa -, který napasujeme na data vzorku. Pokud tento model přiměřeně odpovídá údajům, tj. pokud dokáže aproximovat způsob, jakým se údaje mění, pak předpokládáme, že dokáže aproximovat i chování populace. Model pak poskytuje základ pro rozhodování o populaci, například identifikací vzorců, vysvětlením variability a předpovědí budoucích hodnot. Tento postup může samozřejmě fungovat pouze tehdy, pokud lze data vzorku považovat za reprezentativní pro populaci.
Někdy, i když víme, že vzorek nebyl vybrán náhodně, můžeme jej přesto modelovat. Pak sice nemůžeme ze vzorku formálně usuzovat na populaci, ale stále můžeme modelovat základní strukturu vzorku. Jedním z příkladů může být pohodlný vzorek – vzorek vybraný spíše z důvodů pohodlnosti než pro své statistické vlastnosti. Při modelování takových vzorků by měly být veškeré výsledky uváděny s upozorněním na omezení jakýchkoli závěrů na objekty podobné těm ve vzorku. Jiným typem příkladu je situace, kdy vzorek zahrnuje celou populaci. Například bychom mohli modelovat data pro všech 50 států Spojených států amerických, abychom lépe porozuměli jakýmkoli vzorcům nebo systematickým souvislostem mezi státy.
Protože skutečný svět může být velmi komplikovaný (ve způsobu, jakým se hodnoty dat mění nebo vzájemně ovlivňují), jsou modely užitečné, protože zjednodušují problémy, takže jim můžeme lépe porozumět (a pak přijímat efektivnější rozhodnutí). Na jedné straně tedy potřebujeme, aby modely byly dostatečně jednoduché, abychom je mohli snadno používat k rozhodování, ale na druhé straně potřebujeme modely, které jsou dostatečně pružné, aby poskytovaly dobré aproximace složitých situací. Naštěstí bylo v průběhu let vyvinuto mnoho statistických modelů, které poskytují účinnou rovnováhu mezi těmito dvěma kritérii. Jedním z takových modelů, který poskytuje dobrý výchozí bod pro složitější modely, jimiž se budeme zabývat později, je normální rozdělení.
Ze statistického hlediska je rozdělení pravděpodobnosti teoretický model, který popisuje, jak se náhodná veličina mění. Pro naše účely představuje náhodná veličina hodnoty dat, které nás zajímají v populaci, například prodejní ceny všech rodinných domů na našem trhu s bydlením. Jedním ze způsobů, jak znázornit rozložení hodnot dat v populaci, je histogram, jak je popsáno v části 1.1. Rozdíl je nyní v tom, že histogram zobrazuje celou populaci, nikoli pouze vzorek. Protože populace je mnohem větší než vzorek, mohou být biny histogramu (po sobě jdoucí rozsahy dat, které tvoří vodorovné intervaly pro sloupce) mnohem menší, například následující obrázek ukazuje histogram pro simulovanou populaci 1 000 prodejních cen.
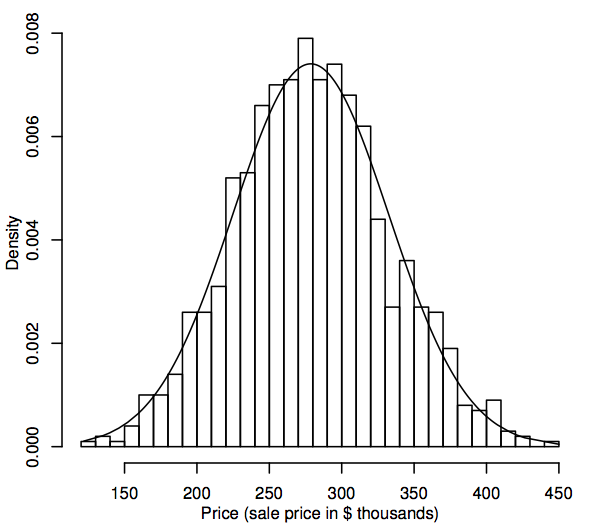
Při zvětšování velikosti populace si můžeme představit, že sloupce histogramu jsou stále tenčí a početnější, až histogram připomíná spíše hladkou křivku než řadu stupňů. Tato hladká křivka se nazývá křivka hustoty a lze si ji představit jako teoretickou verzi populačního histogramu. Křivky hustoty také umožňují vizualizovat pravděpodobnostní rozdělení, například normální rozdělení. Normální křivka hustoty je překryta výše uvedeným histogramem. Simulovaný populační histogram poměrně přesně kopíruje křivku, což naznačuje, že toto simulované populační rozdělení je poměrně blízké normálnímu.
Abychom viděli, jak se teoretické rozdělení může ukázat jako užitečné pro statistické závěry o populacích, jako je tomu v našem příkladu s cenami domů, musíme se blíže podívat na normální rozdělení. Pro začátek uvažujme konkrétní verzi normálního rozdělení, standardní normální rozdělení, které je znázorněno následující křivkou hustoty.
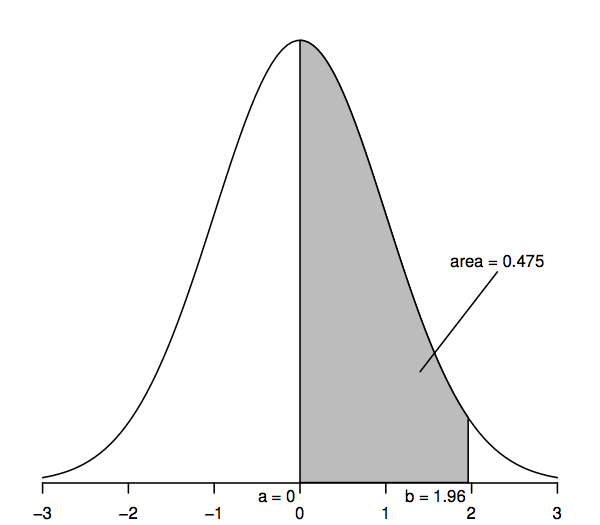
Náhodné proměnné, které se řídí standardním normálním rozdělením, mají střední hodnotu 0 (takže křivka je symetrická kolem 0, která je pod nejvyšším bodem křivky) a směrodatnou odchylku 1 (takže křivka má inflexní bod – kde se křivka ohýbá nejprve na jednu a pak na druhou stranu – v bodech +1 a -1). Křivka normální hustoty se někdy nazývá „zvonová křivka“, protože její tvar připomíná tvar zvonu.
Klíčovou vlastností křivky normální hustoty, která nám umožňuje činit statistické závěry, je, že plochy pod křivkou představují pravděpodobnosti. Celá plocha pod křivkou je jedna, zatímco plocha pod křivkou mezi jedním bodem na vodorovné ose (řekněme a) a jiným bodem (řekněme b) představuje pravděpodobnost, že náhodná veličina, která se řídí standardním normálním rozdělením, je mezi a a b. Takže například obrázek výše ukazuje, že pravděpodobnost je 0.475, že standardní normální náhodná veličina leží mezi a=0 a b=1,96, protože plocha pod křivkou mezi a=0 a b=1,96 je 0,475.
Hodnoty těchto ploch nebo pravděpodobností můžeme získat z různých zdrojů: z tabulek čísel, kalkulaček, tabulkového nebo statistického softwaru, webových stránek atd. Níže otiskujeme pouze několik vybraných hodnot, protože většina pozdějších výpočtů používá zobecnění normálního rozdělení zvané „t-rozdělení“. Také spíše než o oblastech, jako je ta vystínovaná na obrázku výše, bude užitečnější uvažovat o „chvostových oblastech“ (např, vpravo od bodu b), a proto pro konzistenci s pozdějšími tabulkami čísel umožňuje následující tabulka výpočet takových chvostových ploch:
Konkrétně plocha horního chvostu vpravo od 1,96 je 0,025; to je ekvivalentní tvrzení, že plocha mezi 0 a 1,96 je 0,475 (protože celá plocha pod křivkou je 1 a plocha vpravo od 0 je 0,5). Podobně plocha dvou ocásků, která je součtem ploch napravo od 1,96 a nalevo od -1,96, je dvakrát 0,025, tedy 0,05.
Jak nám to všechno pomáhá dělat statistické závěry o populacích, jako je ta v našem příkladu s cenami domů? Základní myšlenka spočívá v tom, že na naše výběrová data napasujeme model normálního rozdělení a tento model pak použijeme k vyvození závěrů o příslušné populaci. Například můžeme použít výpočty pravděpodobnosti pro normální rozdělení (jak je znázorněno na obrázku výše), abychom učinili pravděpodobnostní výroky o populaci modelované pomocí tohoto normálního rozdělení – jak přesně to udělat, si ukážeme v části 1.3. Než to však uděláme, pozastavíme se u jednoho aspektu této odvozovací posloupnosti, který může celý proces rozhodnout nebo zničit. Poskytuje model dostatečně blízkou aproximaci vzorce hodnot vzorku, abychom si mohli být jisti, že model adekvátně reprezentuje hodnoty populace? Čím lepší bude aproximace, tím spolehlivější budou naše inferenční výroky.
Předtím jsme viděli, že křivku hustoty si lze představit jako histogram s velmi velkou velikostí vzorku. Jedním ze způsobů, jak posoudit, zda se naše populace řídí modelem normálního rozdělení, je tedy sestrojit histogram z našich výběrových dat a vizuálně určit, zda „vypadá normálně“, tj. přibližně symetricky a zvonovitě. Jedná se o poněkud subjektivní rozhodnutí, ale se zkušenostmi byste měli zjistit, že je snazší rozeznat jasně nenormální histogramy od těch, které jsou přiměřeně normální. Například zatímco výše uvedený histogram jasně vypadá jako normální křivka hustoty, normalita histogramu 30 vzorových prodejních cen v části 1.1 je méně jistá. Rozumným závěrem by v tomto případě bylo, že i když tento výběrový histogram není dokonale symetrický a zvonovitý, je dostatečně blízko tomu, aby odpovídající (hypotetický) populační histogram mohl být normální.
Alternativním způsobem, jak posoudit normalitu, je sestrojit QQ-plot (kvantil-kvantilový graf), známý také jako normální pravděpodobnostní graf, jak je znázorněno zde pro údaje o cenách domů:
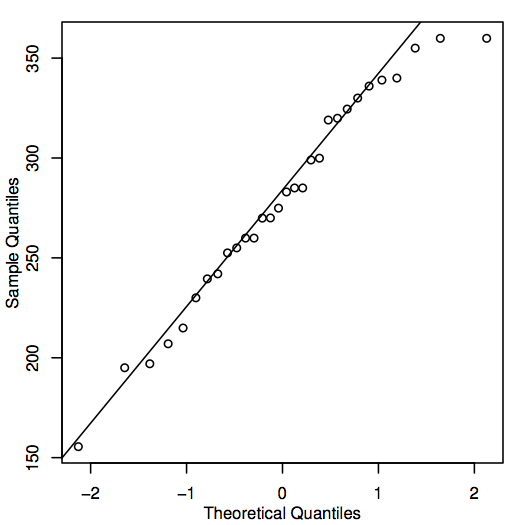
Pokud body v QQ-plotu leží blízko diagonální přímky, pak by odpovídající populační hodnoty mohly být dobře normální. Pokud body obecně leží daleko od přímky, pak je normalita sporná. Opět se jedná o poněkud subjektivní rozhodnutí, které se se zkušenostmi stává snadnějším. V tomto případě, vzhledem k poměrně malému rozsahu vzorku, jsou body pravděpodobně dostatečně blízko přímky, takže je rozumné dojít k závěru, že populační hodnoty by mohly být normální.
Existuje také řada kvantitativních metod pro posouzení normality – viz kapitola 6.3.
.