V tomto článku vysvětlím, jak jsou 2D konvoluce implementovány jako násobení matic. Toto vysvětlení vychází z poznámek předmětu CS231n Konvoluční neuronové sítě pro vizuální rozpoznávání (modul 2). Předpokládám, že čtenář je obeznámen s pojmem operace konvoluce v kontextu hluboké neuronové sítě. Pokud ne, na tomto repozitáři najdete zprávu a vynikající animace vysvětlující, co to konvoluce jsou. Kód pro reprodukci výpočtů v tomto článku si můžete stáhnout zde.

Malý příklad

Předpokládejme, že máme jednokanálový 4 x 4 obraz X a hodnoty jeho pixelů jsou následující:

Dále předpokládejme, že definujeme 2D konvoluci s následujícími vlastnostmi:

To znamená, že bude existovat 9 obrazových políček 2 x 2, která budou elementárně vynásobena maticí W, takto:

Tyto obrazové skvrny lze reprezentovat jako čtyřrozměrné sloupcové vektory a spojit je do jedné matice 4 x 9, P, takto:

Všimněte si, že i-tý sloupec matice P je ve skutečnosti i-té obrazové políčko ve formě sloupcového vektoru.

Matrici vah pro konvoluční vrstvu, W, lze zploštit na čtyřrozměrný řádkový vektor , K, takto:

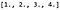
Pro provedení konvoluce nejprve maticově vynásobíme K s P, abychom získali 9rozměrný řádkový vektor (matice 1 x 9), který nám dává:

Poté přetvoříme výsledek K P na správný tvar, což je matice 3 x 3 x 1 (poslední rozměr kanálu). Rozměr kanálu je 1, protože jsme nastavili výstupní filtry na 1. Výška a šířka je 3, protože podle poznámek CS231n:

To znamená, že výsledek konvoluce je:

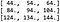
Který se ověří, pokud provedeme konvoluci pomocí vestavěných funkcí PyTorchu (podrobnosti viz doprovodný kód tohoto článku).

Větší příklad

Příklad v předchozí části předpokládá jeden obrázek a výstupní kanály konvoluce jsou 1. V případě, že konvoluce je provedena v jednom kanálu, je třeba ji provést v jednom kanálu. Co by se změnilo, kdybychom tyto předpoklady zmírnili?

Předpokládejme, že naším vstupem do konvoluce je obrázek 4 x 4 se 3 kanály s následujícími hodnotami pixelů:

Pro naši konvoluci nastavíme, že bude mít stejné vlastnosti jako v předchozí části s tím rozdílem, že její výstupní filtry budou mít hodnotu 2. To znamená, že počáteční matice vah W musí mít tvar (2, 2, 2, 3), tj. (výstupní filtry, výška jádra, šířka jádra, kanály vstupního obrazu). Nastavme W na následující hodnoty:

Všimněte si, že každý výstupní filtr bude mít své vlastní jádro (proto máme v tomto příkladu 2 jádra) a kanál každého jádra je 3 (protože vstupní obraz má 3 kanály).

Protože stále konvolujeme jádro 2 x 2 na obrázku 4 x 4 s nulovou výplní a krokem 1, počet obrazových políček je stále 9. Matice obrazových políček P však bude jiná. Přesněji řečeno, i-tý sloupec P bude součet hodnot 1., 2. a 3. kanálu (jako sloupcový vektor) odpovídající obrazovému políčku i. P bude nyní matice 12 x 9. Řádků je 12, protože každá obrazová skvrna má 3 kanály a každý kanál má 4 prvky, protože jsme nastavili velikost jádra na 2 x 2. Takto vypadá matice P:

Stejně jako v případě W bude každé jádro zploštěno na řádkový vektor a spojeno po řádcích do matice 2 x 12, K. I-tý řádek matice K je konkatenace hodnot 1., 2. a 3. kanálu (ve formě řádkového vektoru) odpovídajících i-tému jádru. Takto bude vypadat matice K:

Nyní zbývá jen provést násobení matice K P a přetvořit ji do správného tvaru. Správný tvar je matice 3 x 3 x 2 (rozměr kanálu je poslední). Zde je výsledek násobení:

A zde je výsledek po přetvoření na matici 3 x 3 x 2. Zde je výsledek násobení:

Který se opět ověří, pokud budeme konvoluci provádět pomocí vestavěných funkcí PyTorchu (podrobnosti viz doprovodný kód tohoto článku).

Tak co?“

Proč by nás mělo zajímat vyjadřování 2D konvolucí pomocí násobení matic? Kromě toho, že máme efektivní implementaci vhodnou pro běh na GPU, nám znalost tohoto přístupu umožní uvažovat o chování hluboké konvoluční neuronové sítě. Například He et. al. (2015) vyjádřili 2D konvoluce v termínech násobení matic, což jim umožnilo použít vlastnosti náhodných matic/vektorů k argumentaci pro lepší inicializační rutinu vah.

Závěr

V tomto článku jsem na dvou malých příkladech vysvětlil, jak provádět 2D konvoluce pomocí násobení matic. Doufám, že vám to postačí k zobecnění na libovolné rozměry vstupního obrazu a vlastnosti konvoluce. Pokud vám něco není jasné, dejte mi vědět v komentářích.

1D konvoluce

Metoda popsaná v tomto článku se dá zobecnit i na 1D konvoluce.

Předpokládejme například, že vaším vstupem je 3kanálový 12rozměrný vektor takto:

Pokud naší 1D konvoluci nastavíme následující parametry:

• velikost jádra: 1 x 4
• výstupní kanály: 2
• pruh: 2
• podložení: W bude tenzor ve tvaru (2 , 3, 1, 4): 0
• přesah: 0

Poté budou parametry v konvoluční operaci W. Nastavme W následující hodnoty:

Na základě parametrů operace konvoluce bude mít matice „obrazových“ políček P, tvar (12, 5) (5 obrazových políček, kde každé políčko je 12-D vektor, protože políčko má 4 prvky přes 3 kanály) a bude vypadat takto:

Dále zploštíme W a dostaneme K, který má tvar (2, 12), protože existují 2 jádra a každé jádro má 12 prvků. Takto vypadá K:

Nyní můžeme vynásobit K s P, čímž dostaneme:

Nakonec přetvoříme K P na správný tvar, což je podle vzorce „obraz“ o tvaru (1, 5). To znamená, že výsledkem této konvoluce je tenzor s tvarem (2, 1, 5), protože výstupní kanály jsme nastavili na hodnotu 2. Takto vypadá konečný výsledek:

Který se podle očekávání ověří, pokud bychom konvoluci provedli pomocí vestavěných funkcí PyTorch.

.