Úvod

Představte si to – dostali jste za úkol předpovědět cenu příštího iPhonu a byla vám poskytnuta historická data. Ta zahrnují charakteristiky, jako jsou čtvrtletní tržby, měsíční výdaje a celá řada věcí, které se pojí s bilancí společnosti Apple. Jaký druh problému byste jako datový vědec klasifikovali? Modelování časových řad, samozřejmě.

Od předpovídání prodeje výrobku po odhad spotřeby elektřiny v domácnostech je předpovídání časových řad jednou ze základních dovedností, které by měl každý datový vědec znát, ne-li ovládat. Existuje nepřeberné množství různých technik, které můžete použít, a my se v tomto článku budeme zabývat jednou z nejefektivnějších, která se nazývá Auto ARIMA.

Nejprve pochopíme pojem ARIMA, který nás dovede k našemu hlavnímu tématu – Auto ARIMA. Abychom si pojmy upevnili, vezmeme si datovou sadu a budeme ji implementovat v jazycích Python a R.

Obsah

1. Co je to časová řada
2. Metody prognózování časových řad
3. Úvod do ARIMA
4. Kroky pro implementaci ARIMA
5. Proč potřebujeme AutoARIMA?
6. Implementace auto ARIMA (na souboru dat o cestujících v letecké dopravě)
7. Jak auto ARIMA vybírá parametry

Jestliže jste obeznámeni s časovými řadami a jejich technikami (jako je klouzavý průměr, exponenciální vyhlazování a ARIMA), můžete přeskočit přímo na část 4. Začátečníci mohou začít od následujícího oddílu, který je stručným úvodem do časových řad a různých prognostických technik.

Co je to časová řada ?

Než se seznámíme s technikami práce s daty časových řad, musíme nejprve pochopit, co to vlastně časová řada je a jak se liší od jiných druhů dat. Zde je formální definice časové řady – Je to řada datových bodů měřených v konzistentních časových intervalech. To jednoduše znamená, že konkrétní hodnoty jsou zaznamenávány v konstantním intervalu, který může být hodinový, denní, týdenní, každých 10 dní atd. Časové řady se liší tím, že každý datový bod v řadě je závislý na předchozích datových bodech. Pochopme tento rozdíl jasněji na několika příkladech:

Příklad 1:

Předpokládejme, že máte soubor dat o lidech, kteří si vzali půjčku od určité společnosti (jak je uvedeno v tabulce níže). Myslíte si, že každý řádek bude souviset s předchozími řádky? Určitě ne! Půjčka, kterou si osoba vzala, bude vycházet z jejích finančních podmínek a potřeb (mohou existovat i další faktory, jako je velikost rodiny atd. ale pro zjednodušení uvažujeme pouze příjem a typ půjčky) . Údaje také nebyly shromažďovány v žádném konkrétním časovém intervalu. Záleží na tom, kdy společnost obdržela žádost o úvěr.

Příklad 2:

Uveďme si další příklad. Předpokládejme, že máte datovou sadu, která obsahuje úroveň CO2 ve vzduchu za den (obrázek níže). Budete schopni předpovědět přibližné množství CO2 pro následující den na základě hodnot z několika posledních dnů? Samozřejmě. Pokud si všimnete, data byla zaznamenávána denně, to znamená, že časový interval je konstantní (24 hodin).

Jistě jste již získali intuici – v prvním případě se jedná o jednoduchý regresní problém a ve druhém o problém časové řady. Hádanku časové řady zde sice lze také řešit pomocí lineární regrese, ale to není úplně nejlepší přístup, protože zanedbává souvislost hodnot se všemi relativními minulými hodnotami. Podívejme se nyní na některé běžné techniky používané pro řešení problémů časových řad.

Metody prognózování časových řad

Pro prognózování časových řad existuje řada metod a my se jimi budeme v této části stručně zabývat. Podrobné vysvětlení a kódy v jazyce python pro všechny níže uvedené techniky naleznete v tomto článku:

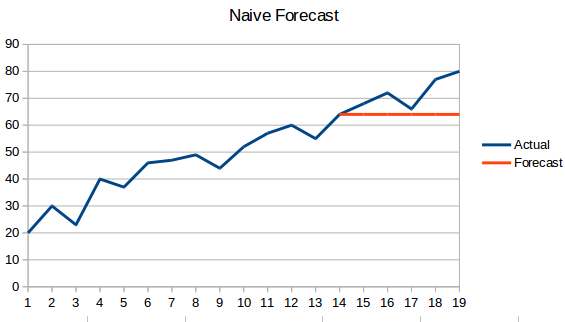
1. Naivní přístup: V této prognostické technice se předpovídá, že hodnota nového datového bodu se bude rovnat hodnotě předchozího datového bodu. Výsledkem by byla plochá přímka, protože všechny nové hodnoty přebírají hodnoty předchozí.
2. Jednoduchý průměr: Další hodnota se bere jako průměr všech předchozích hodnot. Předpovědi jsou zde lepší než u „naivního přístupu“, protože výsledkem není plochá čára, ale zde se berou v úvahu všechny předchozí hodnoty, což nemusí být vždy užitečné. Například při požadavku na předpověď dnešní teploty byste uvažovali spíše teplotu za posledních 7 dní než teplotu před měsícem.
3. Klouzavý průměr : Jedná se o zlepšení oproti předchozí technice. Namísto průměru všech předchozích bodů se za předpovídanou hodnotu bere průměr „n“ předchozích bodů.
4. Vážený klouzavý průměr : Vážený klouzavý průměr je klouzavý průměr, kde je minulým „n“ hodnotám přiřazena různá váha.
5. Jednoduché exponenciální vyhlazování: Při této technice se novějším pozorováním přiřazují větší váhy než pozorováním ze vzdálenější minulosti.
6. Holtův lineární model trendu: Tato metoda zohledňuje trend souboru dat. Trendem rozumíme rostoucí nebo klesající charakter řady. Předpokládejme, že počet rezervací v hotelu se každoročně zvyšuje, pak můžeme říci, že počet rezervací vykazuje rostoucí trend. Prognostická funkce v této metodě je funkcí úrovně a trendu.
7. Holt Wintersova metoda: Tento algoritmus zohledňuje jak trend, tak sezónnost řady. Například – počet rezervací v hotelu je vysoký o víkendech & nízký ve všední dny a každoročně se zvyšuje; existuje týdenní sezónnost a rostoucí trend.
8. ARIMA: ARIMA je velmi populární technika modelování časových řad. Popisuje korelaci mezi datovými body a zohledňuje rozdíl hodnot. Vylepšením ARIMA je SARIMA (neboli sezónní ARIMA). V následující části se ARIMĚ budeme věnovat trochu podrobněji.

Úvod do ARIMY

V této části provedeme stručný úvod do ARIMY, který nám pomůže pochopit Auto Arimu. Podrobné vysvětlení Arimy, parametrů (p,q,d), grafů (ACF PACF) a implementace je součástí tohoto článku : Kompletní tutoriál k časovým řadám.

ARIMA je velmi oblíbená statistická metoda pro předpovídání časových řad. ARIMA je zkratka pro Auto-Regressive Integrated Moving Averages (autoregresivní integrované klouzavé průměry). Modely ARIMA pracují na základě následujících předpokladů –

• Datová řada je stacionární, což znamená, že střední hodnota a rozptyl by se neměly měnit v čase. Řadu lze učinit stacionární pomocí logaritmické transformace nebo diferencováním řady.
• Data poskytnutá jako vstup musí být jednorozměrná řada, protože arima používá minulé hodnoty k předpovědi budoucích hodnot.

ARIMA má tři složky – AR (autoregresní člen), I (diferenční člen) a MA (člen klouzavého průměru). Rozumějme každé z těchto složek –

• AR člen se vztahuje k minulým hodnotám, které se používají pro předpověď příští hodnoty. Termín AR je definován parametrem „p“ ve slově arima. Hodnota parametru ‚p‘ se určuje pomocí grafu PACF.
• TermínMA slouží k definování počtu minulých chyb prognózy použitých k předpovědi budoucích hodnot. Parametr „q“ v arima představuje člen MA. ACF graf se používá k určení správné hodnoty ‚q‘.
• Pořadí diferencování určuje, kolikrát se provede operace diferencování řady, aby byla stacionární. Testy jako ADF a KPSS lze použít k určení, zda je řada stacionární, a pomáhají při identifikaci hodnoty d.

Kroky pro implementaci modelu ARIMA

Obecné kroky pro implementaci modelu ARIMA jsou –

1. Načtení dat: Prvním krokem pro sestavení modelu je samozřejmě načtení souboru dat
2. Předzpracování: V závislosti na souboru dat budou definovány kroky předzpracování. Bude sem patřit vytvoření časových značek, konverze dtypu sloupce datum/čas, vytvoření jednorozměrných řad atd.
3. Vytvoření stacionárních řad: Aby byl splněn předpoklad, je nutné učinit řadu stacionární. To by zahrnovalo kontrolu stacionarity řady a provedení požadovaných transformací
4. Určení hodnoty d: Pro zajištění stacionarity řady se za hodnotu d bude považovat počet opakování rozdílové operace
5. Vytvoření grafů ACF a PACF: Toto je nejdůležitější krok při implementaci ARIMA. Grafy ACF PACF slouží k určení vstupních parametrů pro náš model ARIMA
6. Určete hodnoty p a q. V tomto případě se jedná o grafy ACF a PACF: Hodnoty p a q odečtěte z grafů v předchozím kroku
7. Sestavte model ARIMA: Na základě zpracovaných dat a hodnot parametrů, které jsme vypočítali v předchozích krocích, sestavte model ARIMA
8. Předpovězte hodnoty na validační množině: Předpověď budoucích hodnot
9. Výpočet RMSE: Chcete-li zkontrolovat výkonnost modelu, zkontrolujte hodnotu RMSE pomocí předpovědí a skutečných hodnot na validační množině

Proč potřebujeme model Auto ARIMA?

Ačkoli je ARIMA velmi výkonný model pro předpovídání dat časových řad, procesy přípravy dat a ladění parametrů jsou nakonec opravdu časově náročné. Před implementací modelu ARIMA je třeba zajistit, aby řady byly stacionární, a určit hodnoty p a q pomocí grafů, které jsme probrali výše. Automatická ARIMA nám tento úkol opravdu usnadňuje, protože eliminuje kroky 3 až 6, které jsme viděli v předchozí části. Níže jsou uvedeny kroky, kterými byste se měli řídit při implementaci automatické ARIMY:

1. Načíst data: Tento krok bude stejný. Načtení dat do notebooku
2. Předběžné zpracování dat: Vstupní data by měla být jednorozměrná, proto vynechte ostatní sloupce
3. Fit Auto ARIMA: Fitujte model na jednorozměrné řady
4. Předpovídejte hodnoty na validační množině: Proveďte předpovědi na validační množině
5. Vypočítejte RMSE: Zkontrolujte výkonnost modelu pomocí předpovězených hodnot oproti skutečným hodnotám

Zcela jsme obešli výběr funkce p a q, jak vidíte. Jaká úleva! V další části budeme implementovat automatickou ARIMU s použitím hračkového souboru dat.

Implementace v Pythonu a R

Použijeme soubor dat International-Air-Passenger. Tato datová sada obsahuje měsíční celkové počty cestujících (v tisících). Má dva sloupce – měsíc a počet cestujících. Dataset si můžete stáhnout z tohoto odkazu.

#load the datadata = pd.read_csv('international-airline-passengers.csv')#divide into train and validation settrain = datavalid = data#preprocessing (since arima takes univariate series as input)train.drop('Month',axis=1,inplace=True)valid.drop('Month',axis=1,inplace=True)#plotting the datatrain.plot()valid.plot()

#building the modelfrom pyramid.arima import auto_arimamodel = auto_arima(train, trace=True, error_action='ignore', suppress_warnings=True)model.fit(train)forecast = model.predict(n_periods=len(valid))forecast = pd.DataFrame(forecast,index = valid.index,columns=)#plot the predictions for validation setplt.plot(train, label='Train')plt.plot(valid, label='Valid')plt.plot(forecast, label='Prediction')plt.show()

#calculate rmsefrom math import sqrtfrom sklearn.metrics import mean_squared_errorrms = sqrt(mean_squared_error(valid,forecast))print(rms)

output -76.51355764316357

Níže je uveden kód R pro stejný problém:

# loading packageslibrary(forecast)library(Metrics)# reading datadata = read.csv("international-airline-passengers.csv")# splitting data into train and valid setstrain = datavalid = data# removing "Month" columntrain$Month = NULL# training modelmodel = auto.arima(train)# model summarysummary(model)# forecastingforecast = predict(model,44)# evaluationrmse(valid$International.airline.passengers, forecast$pred)

Jak Auto Arima vybere nejlepší parametry

V uvedeném kódu jsme jednoduše použili .fit() příkaz pro fitování modelu, aniž bychom museli vybírat kombinaci parametrů p, q, d. Jak ale model zjistil nejlepší kombinaci těchto parametrů? Automatická ARIMA bere v úvahu vygenerované hodnoty AIC a BIC (jak můžete vidět v kódu), aby určila nejlepší kombinaci parametrů. Hodnoty AIC (Akaikeho informační kritérium) a BIC (Bayesovo informační kritérium) jsou odhady pro porovnání modelů. Čím nižší jsou tyto hodnoty, tím lepší je model.

Podívejte se na tyto odkazy, pokud vás zajímá matematika za AIC a BIC.

Závěrečné poznámky a další čtení

Zjistil jsem, že auto ARIMA je nejjednodušší technika pro provádění předpovědí časových řad. Znát zkratku je dobré, ale znát matematiku, která za ní stojí, je také důležité. V tomto článku jsem zběžně popsal, jak ARIMA funguje, ale nezapomeňte si projít odkazy uvedené v článku. Pro vaši snadnou orientaci jsou zde opět odkazy:

• Kompletní průvodce pro začátečníky prognózováním časových řad v Pythonu
• Kompletní výukový program k časovým řadám v R
• 7 technik pro prognózování časových řad (s kódy v Pythonu)

Rad bych doporučil procvičit si to, co jsme se zde naučili, na této cvičné úloze: Time Series Practice Problem. Můžete také absolvovat náš výukový kurz vytvořený na stejném cvičném problému: Prognózování časových řad, který vám poskytne náskok.