(IUCr) Symboly pro prvky symetrie

Acta Cryst. (1992). A48, 727-732

Závěrečná zpráva ad hoc výboru Mezinárodní krystalografické unie pro názvosloví symetrie*

P. M. DE WOLFF (předseda), Meermanstraat 126, 2614 AM Delft, Nizozemsko,

Y. BILLIET, Ecole Nationale d’Ingénieurs, BPW 3038 Sfax, Tunesië,

J. D. H. DONNAY, Department of Geological Sciences, McGill University, 3450 University Street, Montreal, Kanada H3A 2A7,

W. FISCHER, Institut für Mineralogie, Petrologie und Kristallographie der Phillips-Universität, Lahnberge, D-3550 Marburg (Lahn), Německo,

R. B. GALIULIN, Institute of Crystallography, Academy of Sciences of Russia, Leninsky Prospekt 59, Moscow 117333, Russia,

A. M. GLAZER, Clarendon Laboratory, University of Oxford, Parks Road, Oxford OX1 3PU England,

TH. HAHN, Institut für Kristallographie, RWTH, Templergraben 55, D-5100 Aachen, Německo,

MARJORIE SENECHAL, Department of Mathematics, Smith College, Northampton, MA 01063, USA,

D. P. SHOEMAKER, katedra chemie, Oregon State University, OR 97331, USA,

H. WONDRATSCHEK, Institut für Kristallographie, Universität Karlsruhe, Kaiserstrasse 12, D-7500 Karlsruhe 1, Německo,

A. J. C. WILSON (ex officio, IUCr Commission on International Tables), Crystallographic Data Centre, University Chemistry Laboratory, Lensfield Road, Cambridge CB2 1EW, England

AND S. C. ABRAHAMS (ex officio, IUCr Commission on Crystallographic Nomenclature), Department of Physics, Southern Oregon State College, 1250 Siskiyou Boulevard, Ashland, OR 97520-5047, USA

(přijato 7. listopadu 1991; přijato 9. března 1992)

* Jmenován 14. listopadu 1984, změněn 10. srpna 1987 podle základních pravidel uvedených v Acta Cryst. (1979), A35, 1072. Závěrečná zpráva přijata 23. prosince 1991 komisí IUCr pro krystalografické názvosloví a 9. března 1992 výkonným výborem.

Abstrakt

Nové nebo nově definované tiskové symboly jsou navrženy ve světle nedávno přijaté nové definice prvků symetrie . Zejména písmeno e pokrývá některé klouzavé roviny, které dosud neměly jedinečný symbol, například ty, které se nazývají „buď a, nebo b“. Doporučuje se používat e v Hermannově-Mauguinově symbolu pěti různých prostorových skupin. Pro roviny e promítané ve směru rovnoběžném s rovinou je navržen grafický symbol, který odstraňuje nejednoznačnost jejich současného označení. Pro nově definovanou třídu klouzavých rovin, které dosud neměly specifický symbol, je navrženo písmeno k. Symboly pro operace symetrie zavedené v popisech prostorových skupin v International Tables for Crystallography (1989), Vol. A (Dordrecht: Kluwer Academic Publishers) se doporučují pro obecné použití, pouze s úpravami pro operace klouzavých odrazů.

Úvod

Ad-hoc výbor jmenovaný v roce 1980, aby zvážil „problémy nomenklatury týkající se operací symetrie a prvků symetrie v prostorových skupinách“, vydal dvě zprávy nazvané Nomenclature for Crystal Families, Bravais-Lattice Types and Arithmetic Classes (de Wolff et al., 1985) a Definice prvků symetrie v prostorových skupinách a bodových skupinách (de Wolff et al., 1989). Jak je uvedeno ve Zprávě z roku 1989, jediným nevyřešeným problémem týkajícím se operací symetrie je výběr vhodných symbolů, protože tento pojem je jasný. V Mezinárodních krystalografických tabulkách (1983, 1989) byl přijat prozatímní zápis, na který se dále odkazuje jako na ITA83.

Printed symbols for symmetry elements

V celé této Zprávě bude použita definice symetrických prvků uvedená ve Zprávě z roku 1989 (de Wolff et al.). Zde zopakujeme podstatu:

Pro každou danou operaci symetrie je definován její geometrický prvek (rovina, bod a/nebo přímka). Symetrický prvek je kombinací geometrického prvku jedné ze symetrických operací v dané prostorové skupině s množinou (nazývanou `množina prvků´) všech symetrických operací v této prostorové skupině, které sdílejí tento geometrický prvek.

Výslovné definice geometrických prvků a popisy z nich vyplývajících symetrických prvků, jakož i jejich symboly jsou uvedeny v tabulkách 1 a 2. (Ty jsou totožné s tabulkami 1 a 2 ve Zprávě z roku 1989 s výjimkou klouzavých rovin a pro úplnost je zde opakujeme, viz níže). Každý prvek symetrie je reprezentován symbolem složeným ze dvou znaků. Prvním znakem je velké písmeno E pro všechny prvky symetrie. Slouží k tomu, aby bylo zřejmé, že se symbol vztahuje k symetrickému prvku, a nikoli například k symetrické operaci. Pokud je to zřejmé již z kontextu, lze písmeno E vynechat, např. „osa 2“ místo „osa E2“.

Tabulka 1. Geometrické prvky operací symetrie v bodových a prostorových skupinách
Operace symetrie	Geometrický prvek	Doplňkové parametry
Identita	Nevyžaduje se	Není
Překlad	Nevyžaduje se	Vektor $\mathbf{t}$
Odraz v rovině A	Rovina A	Nic
Odraz = odraz v rovině A a translace $\mathbf{v}$ rovnoběžný s A	Rovina A	Posuvný vektor $\mathbf{v}$
Rotace kolem přímky b	Přímka b	Úhel a smysl otáčení
Otáčení šroubem = otáčení kolem přímky b a translace $\mathbf{u}$ rovnoběžně s b	Přímka b	Úhel a smysl otáčení šroubového vektoru $\mathbf{u}$
Rotoinverze = otáčení kolem přímky b a inverze přes bod P na b	Přímka b a bod P na b	Úhel (nerovná se $\pi$ ) a smysl otáčení
Inverze přes bod P	Bod P	Nic

Symbol Eg uvedený ve zprávě z roku 1989 lze použít pro klouzavé roviny, pokud chceme pouze ukázat, že prvek symetrie je klouzavá rovina. Na druhou stranu, pokud patří k některému ze speciálních druhů, které se již dlouho označují příslušným písmenem (a, b, c, n nebo d; srov. ITA83), pak toto písmeno nahrazuje g ve slově Eg.

Tabulka 2. Symetrické prvky v bodových a prostorových skupinách
Název symetrického prvku	Symbol	Geometrický prvek	Definiční operace (d.o.)	Operace v množině prvků
Zrcadlová rovina	Em	Rovina A	Odraz v A	D.o. a její koplanární ekvivalenty*
Zrcadlová rovina	Eg $\ddag$	Rovina A	Zrcadlový odraz v A, 2v (ne v) mřížkový překlad	D.o. a její koplanární ekvivalenty*
Osa rotace	En	Přímka b	Rotace kolem b, úhel $2\pi/n$ ,n = 2, 3, 4 nebo 6	1., $\dots$ ,(n – 1)th mocniny d.o. a jejich souosé ekvivalenty $\dag$
Osa šroubu	Enj	Přímka b	Otočení šroubu kolem b, úhel $2\pi/n$ , u =j/n krát nejkratší mřížka translace podél b, pravý šroub; n = 2, 3, 4 nebo 6, $j=1,\dots,(n-1)$	1., $\dots$ ,(n – 1)th mocniny d.o. a jejich souosé ekvivalenty $\dag$
Osa rotace	$E\bar n$	Přímka b a bod P na b	Rotoinverze: rotace kolem b, úhel $2\pi/n$ a inverze přes P; n = 3, 4 nebo 6	D.o. a její inverze
Centrum	$E\bar 1$	Bod P	Inverze přes P	D.o. pouze

* Tj. všechny klouzavé odrazy se stejnou rovinou odrazu, přičemž klouzavé vektory se liší od vektoru d.o. (který je pro odraz považován za nulový) o mřížkový translační vektor.
$\dag$ To jsou všechny rotace a šroubové rotace se stejnou osou b, stejným úhlem a smyslem otáčení a stejným šroubovým vektorem $\mathbf{u}$ (nulovým pro rotaci) až na mřížkový translační vektor.
$\ddag$ V Eg se g nahrazuje a, b, c, n, d, e nebo k pro určité druhy klouzavých rovin, viz §2.

Lze však poukázat na důležitý nový aspekt symbolů typu Eb. Podle ITA83 označování roviny pomocí b pouze znamenalo, že klouzavý odraz v rovině s klouzavou složkou b/2 podél osy b je symetrická operace. Tato definice jistě platí pro situaci zobrazenou na obr. 1.

Obr. 1. (Podle W. Fischera.) Množina prvků klouzavé roviny Eb, zobrazená jako množina bodů nad (+) a pod (-) rovinou vzniklých klouzavými odrazy v rovině, počínaje například znakem + vlevo nahoře. Síť N translací rovnoběžných s rovinou (+ $\cdots$ + vektory) je vyznačena sítí, která je v tomto případě náhodou pravoúhlá. Oba páry hran jsou rovnoběžné s krystalovými osami. Podél osy b se nachází klouzavý odraz s jeho klouzavým vektorem (+ $\cdots$ -).

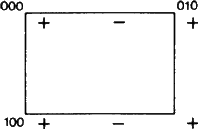
$\begin{figure} \includegraphics {fig1.ps} \end{figure}$

Obr. 1 je stejně jako obr. 2 a 3 převzat ze sady podobných obrázků, které navrhl člen ad-hoc výboru W. Fischer jako soupis všech typů klouzavých ploch. Ačkoli byl tento soubor předložen Výboru v roce 1980, tedy dlouho před vydáním Zprávy z roku 1989, každý z jeho obrázků přesně zobrazuje „soubor prvků“ klouzavé roviny, jak je definován v uvedené Zprávě (viz výše uvedené shrnutí). Pro klouzavou rovinu se množina prvků skládá ze všech klouzavých odrazů, jejichž společným geometrickým prvkem je rovina. Jejich působení je znázorněno v projekci na tuto rovinu. Z výchozí pozice libovolného znaku + vyplývá každý znak – z jednoho z klouzavých odrazů množiny. Všechny jsou zobrazeny v elementární síti výsledného dvourozměrného periodického obrazce znaků + a -.

Často budeme hovořit o síti N tvořené všemi translacemi rovnoběžnými s rovinou; tuto síť si snadno představíme, když se podíváme pouze na znaky +. Tyto vektory je třeba ostře odlišit od vektorů spojujících znak + s libovolným znakem -, z nichž každý je klouzavým vektorem klouzavého odrazu patřícího do množiny prvků.

Nový aspekt vzniká proto, že v některých případech je podle definice ITA83 klouzavá rovina b zároveň klouzavou rovinou a; viz obr. 2. Je zřejmé, že k tomu dochází pouze tehdy, je-li síť N ortogonálně centrovaná, protože pak lze klouzavost a změnit na klouzavost b (a naopak) přidáním centrovací translace. Dosavadní praxe byla takovou klouzavou rovinu libovolně nazývat buď a, nebo b, což způsobovalo neodůvodněné zkreslení a nedostatek jednoznačnosti těchto symbolů. Proto navrhujeme, aby byl případ z obr. 2 pokryt samostatným symbolem.

Obr. 2. (Podle W. Fischera.) Množina prvků roviny Ee-glide. Srov. popisek k obr. 1. Všimněte si, že síť N je zde ortogonálně centrovaná.

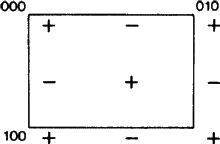
$\begin{figure} \includegraphics {fig2.ps} \end{figure}$

Obsah tohoto symbolu by pak měl být rozšířen na klouzavé roviny v diagonální orientaci, tj. rovnoběžné pouze s jednou krystalovou osou, za předpokladu, že klouzavá rovina má klouzavý vektor podél této osy a že síť N je ortogonálně centrovaná. Pro takové roviny neexistuje dvojznačnost výše uvedené náhodné volby a-b, ale rozšířený rozsah nového symbolu je v souladu s rozsahem všech stávajících symbolů (konkrétně a, b, c, n a d). Každý z nich se používá pro klouzavou rovinu s jednou i dvěma krystalovými osami v síti N, srov. obr. 3.

Pro nový symbol je navrženo písmeno e. Ee se tedy bude používat pro klouzavé roviny s ortogonálními centrovanými sítěmi N a alespoň jedním klouzavým vektorem podél krystalové osy. Je tedy nutné nové kritérium, a to orientace klouzavých vektorů vzhledem ke konvenčním osám krystalu. Protože ty jsou podél směrů symetrie, zatímco každá klouzavá rovina je rovnoběžná se zrcadlovou rovinou mřížky, není překvapivé, že v N je vždy alespoň jedna konvenční osa krystalu. Pokud je taková osa jen jedna, pak kolmo na ni je v N vždy další translace.

Nový symbol e i staré symboly a, b, c, d, n budou nyní nově definovány z hlediska tohoto nového kritéria a Bravaisova typu sítě N. Tato síť je monoklinická nebo ortogonální nebo tetragonální primitivní (mp nebo op nebo tp) nebo ortogonálně centrovaná (oc). Pouze sítě typu oc N umožňují rovinu Ee-glide. Symbol En platí pro sítě N Bravaisova typu mp nebo op, zatímco Ed pro sítě typu oc N. (Jak je uvedeno v poznámce pod čarou k tabulce 1.3 v ITA83: „Klouzavé roviny d se vyskytují pouze v orthorombických prostorových skupinách F, v tetragonálních prostorových skupinách I a v kubických prostorových skupinách I a F . Vyskytují se vždy v párech se střídavými klouzavými vektory“). Na rozdíl od rovin Ea, Eb, Ec a Ee však pro roviny En a Ed neexistuje žádný klouzavý vektor ani rovnoběžný, ani kolmý na konvenční osu v N.

Následné definice klouzavých rovin výše uvedených druhů jsou shrnuty v řádcích (i) a (ii) tabulky 3 a explicitněji na obr. 3.

Tabulka 3. Vytištěné symboly pro speciální druhy klouzavých rovin
Počet klouzavých vektorů rovnoběžných nebo kolmých ke krystalovým osám v síti N	Bravaisův typ sítě N
Symbol je určen podle dvou kritérií. Jedním kritériem je Bravaisův typ (mp, op, tp nebo oc) sítě N tvořené symetrickými translacemi rovnoběžnými s uvažovanou rovinou. Tato síť vždy obsahuje alespoň jednu konvenční krystalovou osu.* Druhé kritérium se týká orientace klouzavých vektorů vzhledem k těmto osám.
	m, op, tp	oc
(i) Jeden nebo dva rovnoběžné	Ec(Ea, Eb)	Ee
(ii) Žádná rovnoběžná, žádná kolmá	En	Ed
(iii) Žádná rovnoběžná, jedna kolmá	Ek	–

* Podle definice v ITA83, § 9.1; pro romboedrické prostorové skupiny se zde však používají pouze hexagonální osy.

Všechny zbývající kluzáky byly dříve bez specifického symbolu. Každá z nich má diagonální orientaci (pouze jedna konvenční krystalová osa v síti N). Mezi klouzavými odrazy v jejich množině prvků není žádný s klouzavým vektorem podél této osy. Jeden klouzavý vektor je však na ni (podle symetrie) kolmý. Symbol se zdá být žádoucí, proto je opět navrženo nové písmeno: k. Nový symbol Ek je stručně definován v řádku (iii) tabulky 3 a je plně znázorněn ve spodním bloku obr. 3. Některé příklady jsou uvedeny v §2.

Obr. 3. (Převzato z nákresů W. Fishera.) Všechny možné aspekty množin prvků klouzavých rovin zobrazené stejně jako na obr. 1, ale nezávisle na označeních os. Diagramy jsou seskupeny do sloupců, v jejichž záhlaví je symbol Bravaisovy sítě (horní čára) jejich sítě N, viz tabulka 3. Ostatní kritéria této tabulky se ověřují tak, že se nejprve podíváme na dvojité čáry znázorňující směry krystalových os v rovině. Jedna hrana (svislá) zobrazené sítě N je vždy zvolena podél takové osy. Druhá hrana je vodorovná s výjimkou případů (1) a (8). U diagramů (1), $\bodů$ ,(5) je symbolem kluzné roviny značka a, b nebo c svislé osy; u ostatních je to zakroužkované písmeno v načrtnutém bloku obsahujícím diagram. Všimněte si svislých klouzavých vektorů v diagramech (1), $\dots$ ,(7), vodorovných v (6), (7), (14), (15) a absence některého z nich v (8), $\dots$ ,(13). Příklad výskytu je uveden pod každým diagramem symbolem prostorové skupiny a trojicí souřadnic roviny.

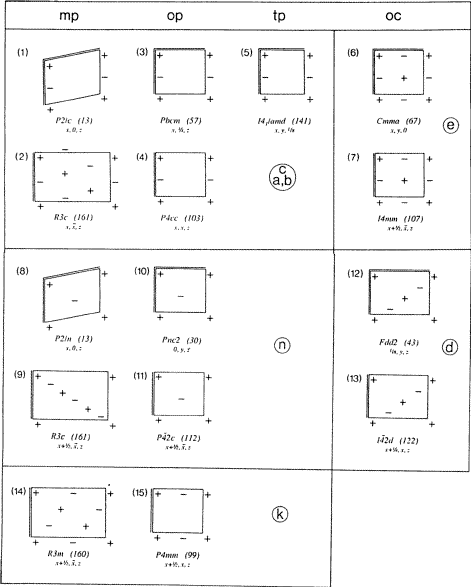
$\begin{figure} \includegraphics {fig3.ps} \end{figure}$

Na obr. 3 je Fischerův soupis všech typů klouzavých rovin zobrazen ve zkrácené – i když stále úplné – podobě, v níž byla krystalovým osám věnována větší grafická pozornost. U každého diagramu je uveden jeden příklad jeho výskytu v prostorové skupině.

V některých romboedrických prostorových skupinách se vyskytují diagonálně orientované roviny Ec, En a Ek se sítěmi mp typu N, které lze popsat trojnásobným centrováním ortogonální sítě. Obdélníková trojitá síť N je pro tyto typy kluzných rovin znázorněna na obr. 3 v diagramech (2), (9) a (14). V diagramu (9) je rozpoznána podobnost s jinými diagramy n, jako je (8) nebo (10), pokud se v (9) uvažuje monoklinická primitivní síť sítě N s diagonálními klouzavými vektory.

Grafické symboly pro prvky symetrie

Stávající grafické symboly, jak jsou definovány a používány v ITA83, považuje ad hoc výbor za vyhovující s jednou výjimkou. Situace je velmi odlišná od tištěných symbolů, protože na výkresech se směr promítání stává přidaným parametrem. V níže použitých termínech „kolmý průmět“ a „rovnoběžný průmět“ se kolmý a rovnoběžný vztahuje k orientaci směru průmětu vzhledem ke klouzavé rovině.

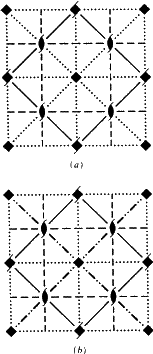
Pro rovinu Ee existuje symbol 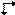pro její kolmý průmět. Existující grafické symboly pro rovnoběžný průmět klouzavé roviny Ee však trpí stejnou nejednoznačností jako tištěné symboly. Vyjadřují klouzavý vektor buď rovnoběžně, nebo kolmo na směr promítání, ale volba je libovolná. Proto je navržen nový symbol pro rovnoběžný průmět klouzavé roviny Ee, a to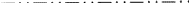

Příklady rovin Ee.

Všechny klouzavé roviny rovnoběžné se dvěma osami v prostorových skupinách Fmm2, Fmmm, $Fm\bar 3$ , $Fm\bar 3m$ a $Fm\bar 3c$ (č. 42, 69, 202, 225 a 226), jakož i některé roviny v pěti prostorových skupinách uvedených v §3.

Diagonálně orientované roviny Ee se vyskytují v prostorových skupinách I4mm, I4cm, $I\bar 42m$ , I4/mmm, I4/mcm, $I\bar 43m$ a $Im\bar 3m$ (č. 1 a 2). 107, 108, 121, 139, 140, 217 a 229).

V ITA83 jsou všechny tyto roviny Ee ve svých rovnoběžných průmětech zakresleny poměrně libovolně jako tečkované nebo čárkované čáry. Na obr. 4 je znázorněn diagram prostorové skupiny I4cm (č. 108), a to jak v ITA83, tak s použitím nového symbolu.

Obr. 4. Schéma prostorové skupiny I4cm (č. 108). (a) Schéma prostorové skupiny I4cm (č. 108) převzaté z ITA83. (b) Totéž, upravené použitím grafického symbolu navrženého v § 2, pro paralelní projekci roviny Ee.

$\begin{figure} \includegraphics {fig4.ps} \end{figure}$

Ačkoli Ek je nový tiskový symbol, v diagramech ITA83 byly všechny kluzné roviny Ek uspokojivě nakresleny se stejnou konvencí, jaká se používá pro kluzné roviny Ea/b/c. Stejně jako v těchto případech existuje jediný speciální klouzavý vektor (kolmý na krystalovou osu v síti N, viz tabulka 3). Pokud je tento vektor například rovnoběžný s rovinou projekce, je rovina Ek vždy nakreslena jako přerušovaná čára předepsaná příslušnou konvencí. Proto se pro kluzné roviny Ek nenavrhuje žádný nový grafický symbol.

Příklady rovin Ek.

Takové roviny lze snadno nalézt v diagramech ITA83 jako roviny rovnoběžné pouze s jednou osou a promítané jako čárkované čáry, např. xxz v P4bm a $P\bar 42_1m$ (č. 100 a 113). Zejména tabulka 3 je přesně v souladu se zobrazeným rozlišením rovin Ek a En. Viz například čárkované a tečkované čáry pro R3m a R3c (č. 160 a 161).

Hermannovy-Mauguinovy symboly prostorové grupy

Znaky objevující se za mřížkovým písmenem v Hermannově-Mauguinově (HM) symbolu prostorové grupy měly původně představovat generující operace grupy. Například b představovalo b-sklopný odraz v rovině orientovaný podle své polohy v symbolu HM.

V praxi se z operací staly oblíbené, i když špatně definované prvky symetrie. Tak se na b začalo pohlížet jako na klouzavou rovinu, Eb v naší současné terminologii. Tato reinterpretace není na škodu s výjimkou případů, kdy operace patří do klouzavé roviny Ee. Platí-li to například pro výše uvedený odraz b-glide, pak v příslušné orientaci existuje Ee, ale ne Eb-glide rovina. V tomto případě se b stává velmi zavádějícím znakem. Kromě toho je zkreslení (dané b oproti a nebo c) stejně rušivé jako v případě symbolů symetrických prvků pojednaných v § 1.

Proto se navrhuje nahradit taková zavádějící písmena a nebo b písmenem e ve všech pěti symbolech HM, v nichž se vyskytují:

Prostorová skupina č. 1.	39	41	64	67	68
Symbol v ITA83:	Abm2	Aba2	Cmca	Cmma	Ccca
Nový symbol:	Aem2	Aea2	Cmce	Cmme	Ccce.

Další výhodou navržených nových symbolů je, že e – na rozdíl od a nebo b – je neutrální, a proto se při permutaci osy nemění.

Tiskové symboly pro operace symetrie

Kompletní sadu tiskových symbolů navrhl W. Fischer & E. Koch (ITA83, §11.2) a byla hojně použita v částech popisů prostorových grup pro operace symetrie.

Krátce řečeno, každý symbol se skládá až ze tří částí. První částí je jeden znak (někdy s indexem), který popisuje druh operace. Následující část (části) udává (udávají) složky příslušného vektoru posunu nebo translace – vždy v závorkách – a souřadnice geometrického prvku operace, a to v tomto pořadí.

Ad hoc výbor si po zvážení tohoto systému přeje zavést dvě úpravy pro posuvné odrazy:

(i) místo současného prvního znaku (kterým může být a, b, c, n, d nebo g) vždy psát písmeno g;

(ii) vždy psát složky posuvného vektoru (v závorkách) v plném znění, zejména pro jednoduché posuvné odrazy v rovinách posuvu a, b nebo c, kde byly dříve vynechány.

Pravidlo (i) potlačuje informaci o druhu klouzavé roviny, do které operace patří. Velmi často je tato informace irelevantní nebo dokonce matoucí. U rovin a/b/c může potlačení zničit podstatnou informaci, ale tato ztráta je obnovena pravidlem (ii), jak je uvedeno v příkladu níže.

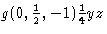Přijetím těchto změn se výrazně zlepšila jednotnost symbolů – také s ohledem na symboly pro rotace. Například symbol klouzavého odrazu v rovině $x = \frac{1}{4}$ s neobvyklým klouzavým vektorem $(0, \frac{1}{2}, -1)$ , totiž $g(0, \frac{1}{2}, 1) \frac{1}{4}yz$ , nyní odpovídá symbolu pro jednoduchý b-klouzavý odraz. Ten byl v ITA83 označen $b \frac{1}{4} y z$ , ale ten je pravidlem (ii) změněn na $g(0, \frac{1}{2}, 0) \frac{1}{4} y z$ .

Výše uvedená pravidla platí i pro klouzavé odrazy patřící do množiny prvků zrcadlové roviny. Pokud je tedy složka posunu takové operace (0, 1, 2), pak její symbol začíná g(0, 1, 2), nikoliv m(0, 1,2).

International Tables for Crystallography (1983). Vol. A, edited by TH. HAHN, zejména §§ 1.1, 1.3, 1.4, 7 a 11. Dordrecht: Kluwer Academic Publishers.

International Tables for Crystallography (1989). Vol. A, 2nd, revised, ed., edited by TH. HAHN. Dordrecht: Kluwer Academic Publishers.

WOLFF, P. M. DE, BELOV, N. V., BERTAUT, E. F., BUERGER, M. J., DONNAY, J. D. H., FISCHER, W., HAHN, TH., KOPTSIK, V. A., MACKAY, A. L., WONDRATSCHEK, H., WILSON, A. J. C. & ABRAHAMS, S. C. (1985). Acta Cryst. A41, 278-280.

WOLFF, P. M. DE, BILLIET, Y., DONNAY, J. D. H., FISCHER, W., GALIULIN, R. B., GLAZER, A. M., SENECHAL, M., SHOEMAKER, D. P., WONDRATSCHEK, H., HAHN, TH., WILSON, A. J. C. & ABRAHAMS, S. C. (1989). Acta Cryst. A45, 494-499.

…vektory. Symboly kluzných rovin c, n a k pro tři diagramy (2), (9) a (14) na obr. 3 byly samozřejmě přiřazeny podle tabulky 3. Jeden člen ad-hoc komise (profesor Wondratschek) se domnívá, že symbol n pro diagram (9) je v rozporu s tradičními představami o n rovinách. Navrhuje přiřadit diagramu (9) zvláštní symbol. Tento návrh však nezískal v rámci ad-hoc výboru dostatečnou podporu.

Symboly pro prvky symetrie a operace symetrie