Mens metoderne i det foregående afsnit er nyttige til at beskrive og vise stikprøvedata, viser statistikkens virkelige styrke sig, når vi bruger stikprøver til at give os oplysninger om populationer. I denne sammenhæng er en population hele samlingen af objekter af interesse, f.eks. salgspriserne for alle enfamiliehuse på boligmarkedet, der er repræsenteret af vores datasæt. Vi vil gerne vide mere om denne population for at kunne træffe en beslutning om, hvilket hus vi skal købe, men de eneste data, vi har, er en tilfældig stikprøve på 30 salgspriser.

Nu kan vi dog anvende “statistisk tænkning” til at drage konklusioner om den population, vi er interesseret i, ved at analysere stikprøvedataene. Vi anvender især begrebet model – en matematisk abstraktion af den virkelige verden – som vi tilpasser til stikprøvedataene. Hvis denne model giver en rimelig tilpasning til dataene, dvs. hvis den kan tilnærme sig den måde, hvorpå dataene varierer, antager vi, at den også kan tilnærme sig befolkningens adfærd. Modellen danner så grundlaget for at træffe beslutninger om populationen, f.eks. ved at identificere mønstre, forklare variation og forudsige fremtidige værdier. Denne proces kan naturligvis kun fungere, hvis stikprøvedataene kan betragtes som repræsentative for populationen.

Sommetider, selv når vi ved, at en stikprøve ikke er blevet udvalgt tilfældigt, kan vi stadig modellere den. I så fald kan vi måske ikke formelt udlede noget om en population ud fra stikprøven, men vi kan stadig modellere den underliggende struktur i stikprøven. Et eksempel herpå er en bekvemmelighedsstikprøve – en stikprøve, der er udvalgt mere af bekvemmelighedshensyn end på grund af dens statistiske egenskaber. Ved modellering af sådanne stikprøver bør alle resultater rapporteres med en advarsel om at begrænse eventuelle konklusioner til objekter, der ligner dem, der indgår i stikprøven. En anden type eksempel er, når stikprøven omfatter hele populationen. Vi kunne f.eks. modellere data for alle 50 stater i USA for bedre at forstå eventuelle mønstre eller systematiske sammenhænge mellem staterne.

Da den virkelige verden kan være ekstremt kompliceret (i den måde, hvorpå dataværdier varierer eller interagerer sammen), er modeller nyttige, fordi de forenkler problemerne, så vi bedre kan forstå dem (og derefter træffe mere effektive beslutninger). På den ene side har vi derfor brug for modeller, der er enkle nok til, at vi let kan bruge dem til at træffe beslutninger, men på den anden side har vi brug for modeller, der er fleksible nok til at give gode tilnærmelser til komplekse situationer. Heldigvis er der i årenes løb blevet udviklet mange statistiske modeller, som giver en effektiv balance mellem disse to kriterier. En sådan model, som giver et godt udgangspunkt for de mere komplicerede modeller, som vi senere overvejer, er normalfordelingen.

Fra et statistisk perspektiv er en sandsynlighedsfordeling en teoretisk model, der beskriver, hvordan en tilfældig variabel varierer. Til vores formål repræsenterer en tilfældig variabel de dataværdier af interesse i populationen, f.eks. salgspriserne på alle enfamiliehuse på vores boligmarked. En måde at repræsentere fordelingen af dataværdier i populationen på er i et histogram, som beskrevet i afsnit 1.1. Forskellen er nu, at histogrammet viser hele populationen i stedet for kun stikprøven. Da populationen er så meget større end stikprøven, kan histogrammets bins (de på hinanden følgende områder af dataene, der udgør de vandrette intervaller for søjlerne) være meget mindre, f.eks. viser følgende et histogram for en simuleret population på 1.000 salgspriser.

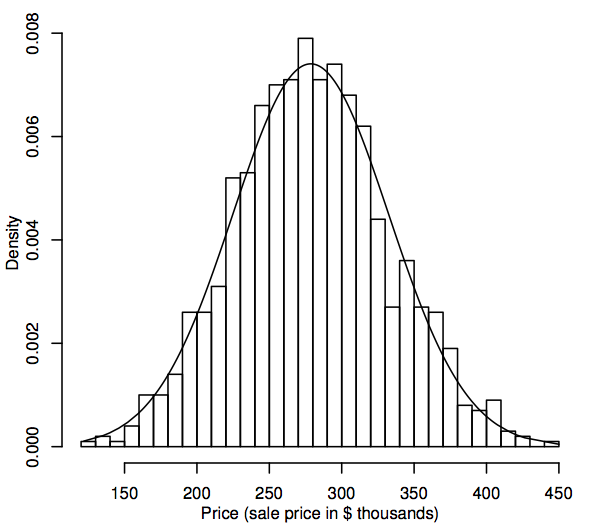
Når populationens størrelse bliver større, kan vi forestille os, at histogrammernes søjler bliver tyndere og flere, indtil histogrammet ligner en jævn kurve i stedet for en række trin. Denne glatte kurve kaldes en tæthedskurve og kan opfattes som den teoretiske udgave af populationshistogrammet. Tæthedskurver giver også en måde at visualisere sandsynlighedsfordelinger som f.eks. normalfordelingen. En normal tæthedskurve er lagt oven på histogrammet ovenfor. Det simulerede befolkningshistogram følger kurven ret tæt, hvilket tyder på, at denne simulerede befolkningsfordeling ligger ret tæt på normalfordelingen.

For at se, hvordan en teoretisk fordeling kan vise sig nyttig til at foretage statistiske slutninger om befolkninger som den i vores eksempel med boligpriserne, skal vi se nærmere på normalfordelingen. Til at begynde med betragter vi en bestemt udgave af normalfordelingen, standardnormalfordelingen, som er repræsenteret ved følgende tæthedskurve.

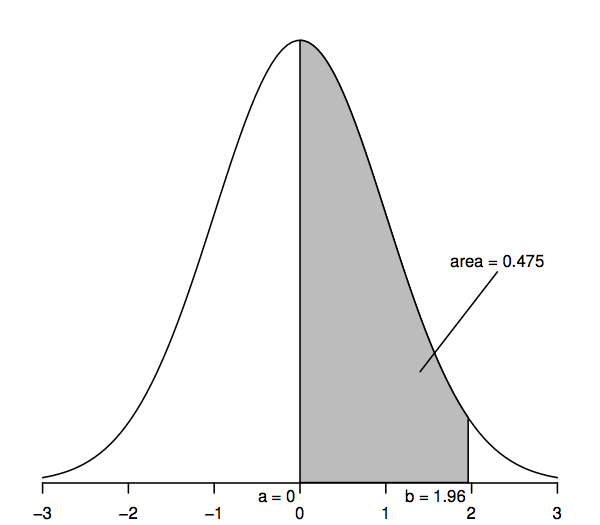
Lokalvariabler, der følger en standardnormalfordeling, har en middelværdi på 0 (så kurven er symmetrisk omkring 0, som ligger under kurvens højeste punkt) og en standardafvigelse på 1 (så kurven har et bøjningspunkt – hvor kurven først bøjer den ene vej og derefter den anden – ved +1 og -1). Den normale tæthedskurve kaldes undertiden for “klokkekurven”, da dens form ligner en klokke.

Den vigtigste egenskab ved den normale tæthedskurve, som gør det muligt at foretage statistiske slutninger, er, at områderne under kurven repræsenterer sandsynligheder. Hele arealet under kurven er 1, mens arealet under kurven mellem et punkt på den vandrette akse (f.eks. a) og et andet punkt (f.eks. b) repræsenterer sandsynligheden for, at en tilfældig variabel, der følger en standardnormalfordeling, ligger mellem a og b. Så f.eks. viser figuren ovenfor, at sandsynligheden er 0.475 for, at en standardnormal tilfældig variabel ligger mellem a=0 og b=1,96, da arealet under kurven mellem a=0 og b=1,96 er 0,475.

Vi kan få værdier for disse arealer eller sandsynligheder fra en række forskellige kilder: taltabeller, lommeregnere, regneark eller statistisk software, websteder osv. Nedenfor udskriver vi kun nogle få udvalgte værdier, da de fleste af de senere beregninger anvender en generalisering af normalfordelingen kaldet “t-fordelingen”. Desuden vil det i stedet for områder som det skraverede i figuren ovenfor blive mere nyttigt at betragte “haleområder” (f.eks, til højre for punkt b), og af hensyn til konsistensen med senere taltabeller giver følgende tabel mulighed for at beregne sådanne haleområder:

I særdeleshed er det øverste haleområde til højre for 1,96 0,025; dette svarer til at sige, at området mellem 0 og 1,96 er 0,475 (da hele området under kurven er 1, og området til højre for 0 er 0,5). På samme måde er arealet med to haler, som er summen af arealerne til højre for 1,96 og til venstre for -1,96, to gange 0,025 eller 0,05.

Hvordan hjælper alt dette os med at foretage statistiske slutninger om populationer som i vores eksempel med boligpriser? Den grundlæggende idé er, at vi tilpasser en normalfordelingsmodel til vores stikprøvedata og derefter bruger denne model til at drage konklusioner om den tilsvarende population. Vi kan f.eks. bruge sandsynlighedsberegninger for en normalfordeling (som vist i figuren ovenfor) til at lave sandsynlighedsudsagn om en population, der er modelleret ved hjælp af denne normalfordeling – vi viser præcis, hvordan man gør dette i afsnit 1.3. Inden vi gør det, holder vi dog en pause for at overveje et aspekt af denne slutningssekvens, som kan være afgørende for processen. Giver modellen en tilstrækkelig tæt tilnærmelse til mønstret af stikprøveværdierne til, at vi kan være sikre på, at modellen repræsenterer populationsværdierne på passende vis? Jo bedre tilnærmelse, jo mere pålidelige vil vores inferentielle udsagn være.

Vi så tidligere, hvordan en tæthedskurve kan opfattes som et histogram med en meget stor stikprøvestørrelse. Så en måde at vurdere, om vores population følger en normalfordelingsmodel, er at konstruere et histogram ud fra vores stikprøvedata og visuelt afgøre, om det “ser normalt ud”, dvs. omtrent symmetrisk og klokkeformet. Dette er en noget subjektiv beslutning, men med erfaringen skulle man opdage, at det bliver lettere at skelne klart ikke-normale histogrammer fra dem, der er rimeligt normale. Mens f.eks. histogrammet ovenfor klart ligner en normal tæthedskurve, er det mindre sikkert, at histogrammet over 30 salgspriser i afsnit 1.1 er normalt. En rimelig konklusion i dette tilfælde ville være, at selv om dette prøvehistogram ikke er perfekt symmetrisk og klokkeformet, er det tæt nok på til, at det tilsvarende (hypotetiske) populationshistogram meget vel kunne være normalt.

En alternativ måde at vurdere normaliteten på er at konstruere et QQ-plot (quantile-quantile-plot), også kendt som et normalt sandsynlighedsplot, som vist her for boligprisdataene:

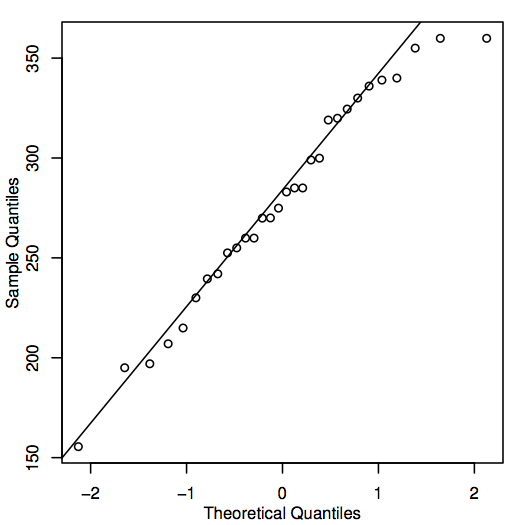
Hvis punkterne i QQ-plottet ligger tæt på den diagonale linje, kan de tilsvarende populationsværdier godt være normale. Hvis punkterne generelt ligger langt fra linjen, så er der tvivl om normaliteten. Igen er dette en noget subjektiv beslutning, som bliver lettere at træffe med erfaringen. I dette tilfælde ligger punkterne i betragtning af den forholdsvis lille stikprøvestørrelse sandsynligvis tæt nok på linjen til, at det er rimeligt at konkludere, at populationsværdierne kunne være normale.

Der findes også en række kvantitative metoder til at vurdere normalitet – se afsnit 6.3.