Definition
Et polynomium i variablen x er en funktion, der kan skrives på formen,
hvor an, an-1 , …, a2, a1, a0 er konstanter. Vi kalder den term, der indeholder den højeste potens af x (dvs. anxn), for den ledende term, og vi kalder an for den ledende koefficient. Graden af polynomiet er potensen af x i den førende term. Vi har allerede set polynomier af grad 0, 1 og 2, som var henholdsvis den konstante, den lineære og den kvadratiske funktion. Polynomier af grad 3, 4 og 5 har også særlige navne: kubiske, kvarte og kvintetiske funktioner. Polynomier med grad n > 5 kaldes blot n-tedegrads polynomier. Navnene på de forskellige polynomiske funktioner er opsummeret i nedenstående tabel.
| Grad af polynomiet | Navn på funktionen |
| 0 | Konstant funktion |
| 1 | Linær funktion |
| 2 | Quadratisk funktion |
| 3 | Kubisk funktion |
| 4 | Quartisk funktion |
| 5 | Quintisk funktion |
| n (hvor n > 5) | polynomium af niende grad |
Nogle eksempler på polynomier omfatter:
Polynomiernes begrænsningsadfærd
En funktions begrænsningsadfærd beskriver, hvad der sker med funktionen, når x → ±∞. Graden af et polynomium og fortegnet på dets ledende koefficient dikterer dets begrænsningsadfærd. Især
Disse resultater er opsummeret i nedenstående tabel.
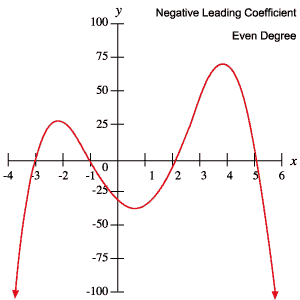
Du kan bruge disse oplysninger til at afgøre, om et polynomium har ulige eller lige grad, og om den ledende koefficient er positiv eller negativ, blot ved at inspicere dets graf.
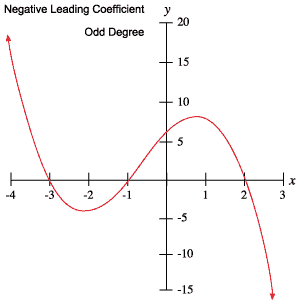
De følgende grafer for polynomier eksemplificerer hver af de adfærdsmønstre, der er skitseret i ovenstående tabel.
Rødder og vendepunkter
Graden af et polynomium fortæller endnu mere om det end den begrænsende adfærd. Nærmere bestemt kan et polynomium af n. grad højst have n reelle rødder (x-intercepts eller nuller), når man tæller multiplikatorerne med. Lad os f.eks. antage, at vi ser på et 6. grads polynomium, der har 4 forskellige rødder. Hvis to af de fire rødder har multiplicitet 2 og de to andre har multiplicitet 1, ved vi, at der ikke er andre rødder, fordi vi har taget højde for alle 6 rødder. Det skyldes, at rødder med en multiplicitet på to (også kendt som dobbeltrødder) tælles som to rødder.
Vær opmærksom på, at et polynomium af n. grad ikke behøver at have n reelle rødder – det kan have færre, fordi det har imaginære rødder. Bemærk, at et polynomium af ulige grad skal have mindst én reel rod, da funktionen nærmer sig – ∞ i den ene ende og + ∞ i den anden ende; en kontinuert funktion, der skifter fra negativ til positiv, må skære x-aksen et sted midt imellem. Desuden kan et polynomium af n. grad højst have n – 1 vendepunkter. Et vendepunkt er et punkt, hvor funktionen skifter fra stigende til aftagende eller fra aftagende til stigende, som det ses i figuren nedenfor. Igen behøver et n-tyvende gradspolynomium ikke nødvendigvis at have n – 1 vendepunkter, det kan have færre.
Advarsel
Det er vigtigt at gøre sig klart, at der er forskel på lige og ulige funktioner og lige og ulige gradspolynomier. Enhver funktion, f(x), er enten lige, hvis,
f(-x) = x,
for alle x i domænet for f(x), eller ulige, hvis,
f(-x) = -x,
for alle x i domænet for f(x), eller hverken lige eller ulige, hvis ingen af de to ovenstående er sande udsagn.
Et k-te gradspolynomium, p(x), siges at have lige grad, hvis k er et lige tal, og ulige grad, hvis k er et ulige tal. Husk, at selv om p(x) har lige grad, er det ikke nødvendigvis en lige funktion. På samme måde er p(x), hvis den har ulige grad, ikke nødvendigvis en ulige funktion.
Vi bruger også udtrykkene lige og ulige til at beskrive rødder af polynomier. Konkret har et polynomium p(x) en rod x = a med multipliciteten k (dvs. x = a er en rod, der gentages k gange), hvis (x – a)k er en faktor af p(x). Vi siger, at x = a har lige multiplicitet, hvis k er et lige tal, og ulige multiplicitet, hvis k er et ulige tal.
Domæne og rækkevidde
Alle polynomier har det samme domæne, som består af alle reelle tal. Området for ulige polynomier af ulige grad består også af alle reelle tal. Området for polynomier af lige grad er en smule mere kompliceret, og vi kan ikke eksplicit angive området for alle polynomier af lige grad. Hvis den ledende koefficient er positiv, vil funktionen strække sig til + ∞; hvis den ledende koefficient er negativ, vil den strække sig til – ∞. Det betyder, at polynomier af lige grad med positiv ledende koefficient har et område, hvor ymax angiver det globale maksimum, som funktionen opnår. Generelt er det ikke muligt analytisk at bestemme polynomiernes maksima eller minima.
*****
I næste afsnit lærer du polynomialdivision, en teknik, der bruges til at finde rødderne af polynomiale funktioner.
Polynomialdivision