En illustreret forklaring på udførelse af 2D-konvolutioner ved hjælp af matrixmultiplikationer

I denne artikel vil jeg forklare, hvordan 2D-konvolutioner implementeres som matrixmultiplikationer. Denne forklaring er baseret på noter fra CS231n Convolutional Neural Networks for Visual Recognition (modul 2). Jeg antager, at læseren er bekendt med begrebet en konvolutionsoperation i forbindelse med et dybt neuralt netværk. Hvis ikke, har denne repo en rapport og fremragende animationer, der forklarer, hvad konvolutioner er. Koden til at reproducere beregningerne i denne artikel kan downloades her.

Lille eksempel

Sæt, vi har et enkeltkanal 4 x 4-billede, X, og dets pixelværdier er som følger:

Sæt endvidere, vi definerer en 2D-foldning med følgende egenskaber:

Egenskaber for den 2D-foldningsoperation, som vi ønsker at udføre på vores billede

Det betyder, at der vil være 9 2 x 2 billedfelter, som vil blive elementvis ganget med matrixen W, på følgende måde:

Alle mulige 2 x 2-billedfelter i X givet parametrene for 2D-foldningen. Hver farve repræsenterer en unik plet

Disse billedpletter kan repræsenteres som 4-dimensionelle kolonnevektorer og sammenkædes for at danne en enkelt 4 x 9-matrix, P, på følgende måde:

Bemærk, at den i-te kolonne i matrix P faktisk er den i-te billedplet i kolonnevektorform.

Matrixen af vægte til konvolutionslaget, W, kan fladtrykkes til en 4-dimensionel rækkevektor , K, på følgende måde:

W som en fladtrykt rækkevektor K

For at udføre konvolutionen skal vi først matrixmultiplicere K med P for at få en 9-dimensionel rækkevektor (1 x 9 matrix), hvilket giver os:

Resultatet af K P

Dernæst omformer vi resultatet af K P til den korrekte form, som er en 3 x 3 x 1 matrix (kanaldimensionen sidst). Kanaldimensionen er 1, fordi vi sætter udgangsfiltrene til 1. Højden og bredden er 3, fordi ifølge CS231n-noterne:

Formel til beregning af højden efter anvendelse af en konvolutionsoperation på et billede. Formlen til beregning af bredden er den samme (erstat blot billedhøjde og kernehøjde med henholdsvis billedbredde og kernebredde

Det betyder, at resultatet af konvolutionen er:

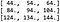
Slutresultatet af at udføre konvolutionen ved hjælp af matrixmultiplikationer

Hvilket tjekker, hvis vi udfører konvolutionen ved hjælp af PyTorch’s indbyggede funktioner (se denne artikels ledsagende kode for detaljer).

Større eksempel

Eksemplet i det foregående afsnit forudsætter et enkelt billede, og udgangskanalerne for konvolutionen er 1. Hvad ville ændre sig, hvis vi lemper disse antagelser?

Lad os antage, at vores input til konvolutionen er et 4 x 4-billede med 3 kanaler med følgende pixelværdier:

Pixelværdier i vores 4 x 4 x 3 indgangsbillede

Vedrørende vores konvolution vil vi indstille den til at have de samme egenskaber som i det foregående afsnit, bortset fra at dens udgangsfiltre er 2. Det betyder, at den oprindelige vægtmatrix, W, skal have formen (2, 2, 2, 2, 3), dvs. (udgangsfiltre, kernehøjde, kernebredde, indgangsbilledets kanaler). Lad os indstille W til at have følgende værdier:

Værdier for W givet en 2 x 2-kernel, 2 udgangsfiltre og et indgangsbillede med 3 kanaler

Bemærk, at hvert udgangsfilter vil have sin egen kerne (hvilket er grunden til, at vi har 2 kerner i dette eksempel), og at hver kernes kanal er 3 (da indgangsbilledet har 3 kanaler).

Da vi stadig konvolverer en 2 x 2 kerne på et 4 x 4 billede med 0 zero-padding og stride 1, er antallet af billedpatches stadig 9. Imidlertid vil matrixen af billedfelter, P, være anderledes. Mere specifikt vil den i-te kolonne i P være sammenkædningen af værdierne for 1., 2. og 3. kanal (som en kolonnevektor) svarende til billedfelt i. P vil nu være en 12 x 9-matrix. Rækkerne er 12, fordi hvert billedfelt har 3 kanaler, og hver kanal har 4 elementer, da vi har sat kernestørrelsen til 2 x 2. Sådan ser P ud:

Som for W vil hver kerne blive fladet ud til en rækkevektor og sammenkædet rækkevis for at danne en 2 x 12 matrix, K. Den i-te række i K er sammenkædningen af den første, anden og tredje kanalværdi (i form af en rækkevektor), der svarer til den i-te kerne. Sådan vil K se ud:

Den 2 x 12 matrix af fladtrykte kerneværdier i W, K

Nu er der kun tilbage at udføre matrixmultiplikationen K P og omforme den til den korrekte form. Den korrekte form er en 3 x 3 x 2-matrix (kanaldimensionen sidst). Her er resultatet af multiplikationen:

Resultatet af K P, en 2 x 9 matrix

Og her er resultatet efter at have omformet den til en 3 x 3 x 3 x 2 matrix:

Det endelige resultat af at udføre konvolutionen ved hjælp af matrixmultiplikationer

Hvilket igen tjekker, hvis vi til at udføre konvolutionen ved hjælp af PyTorchs indbyggede funktioner (se denne artikels ledsagende kode for detaljer).

So What?

Hvorfor skal vi bekymre os om at udtrykke 2D-foldninger i form af matrixmultiplikationer? Ud over at have en effektiv implementering, der er egnet til at køre på en GPU, vil viden om denne fremgangsmåde gøre det muligt for os at ræsonnere om opførslen af et dybt konvolutionelt neuralt netværk. For eksempel har He et. al. (2015) udtrykte 2D-foldninger i form af matrixmultiplikationer, hvilket gjorde det muligt for dem at anvende egenskaberne ved tilfældige matricer/vektorer til at argumentere for en bedre initialiseringsrutine for vægte.

Slutning

I denne artikel har jeg forklaret, hvordan man udfører 2D-foldninger ved hjælp af matrixmultiplikationer ved at gå gennem to små eksempler. Jeg håber, at dette er tilstrækkeligt til, at du kan generalisere til vilkårlige indgangsbilleddimensioner og convolutionsegenskaber. Lad mig vide i kommentarerne, hvis noget er uklart.

1D-konvolution

Metoden beskrevet i denne artikel kan også generaliseres til 1D-konvolutioner.

For eksempel antager vi, at dit input er en 3-kanals 12-dimensionel vektor på følgende måde:

Et input, der er en 12-D vektor med 3 kanaler

Hvis vi indstiller vores 1D-foldning til at have følgende parametre:

kernestørrelse: 1 x 4
udgangskanaler: 2
stride: 2
padding: 0
bias: 0

Så vil parametrene i konvolutionsoperationen, W, være en tensor med formen (2 , 3, 1, 4). Lad os sætte W til at have følgende værdier:

Værdier for W. Bemærk, at hver kerne er en (3, 1, 4)-tensor

Baseret på parametrene for konvolutionsoperationen vil matrixen af “billed”-pletter P have formen (12, 5) (5 billedpletter, hvor hver billedplet er en 12-D vektor, da en plet har 4 elementer på tværs af 3 kanaler) og vil se således ud:

Næst flader vi W ud for at få K, som har form (2, 12), da der er 2 kerner, og hver kerne har 12 elementer. Sådan ser K ud:

Værdier af K, en 2 x 12 matrix

Nu kan vi gange K med P, hvilket giver:

Resultatet af K P, en 2 x 5 matrix

Sluttelig omformer vi K P til den korrekte form, som ifølge formlen er et “billede” med formen (1, 5). Det betyder, at resultatet af denne konvolution er en tensor med formen (2, 1, 5), da vi indstiller udgangskanalerne til 2. Sådan ser det endelige resultat ud:

Resultatet af K P efter omformning til den korrekte form

Hvilket som forventet tjekker, hvis vi skulle udføre konvolutionen ved hjælp af PyTorchs indbyggede funktioner.