Bayesian Belief Network eller Bayesian Network eller Belief Network er en probabilistisk grafisk model (PGM), der repræsenterer betingede afhængigheder mellem tilfældige variabler ved hjælp af en Directed Acyclic Graph (DAG).
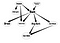
I dag vil jeg forsøge at forklare de vigtigste aspekter af Belief Networks, især for applikationer, som kan være relateret til Social Network Analysis(SNA). Desuden vil jeg vise dig et eksempel på en implementering af denne type netværk.
Hvad bruger vi Bayesian Networks til?
Bayesian Networks anvendes på mange områder. F.eks. sygdomsdiagnose, optimeret web-søgning, spamfiltrering, genreguleringsnetværk osv. Og denne liste kan udvides. Hovedformålet med disse netværk er at forsøge at forstå strukturen af kausalitetsrelationer. For at tydeliggøre dette, lad os overveje et problem med sygdomsdiagnoser. Med givne symptomer og den deraf følgende sygdom konstruerer vi vores Belief Network, og når der kommer en ny patient, kan vi udlede, hvilken sygdom eller hvilke sygdomme den nye patient kan have ved at angive sandsynligheder for hver enkelt sygdom. På samme måde kan disse kausalitetsrelationer konstrueres for andre problemer, og inferenceteknikker kan anvendes til interessante resultater.
Quick Probability Review
Hvor vi fortsætter, lad mig for at genopfriske vores hukommelse give jer definitionen af betinget egenskab. Betinget sandsynlighed er sandsynligheden for en tilfældig variabel, når en anden tilfældig variabel er givet. Den vises ved
Hvis disse to tilfældige variabler er afhængige,
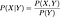
Hvis de er uafhængige, så
Matematisk definition af troværdighedsnetværk
Sandsynlighederne beregnes i trosnetværkene ved følgende formel
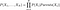
Som du vil forstå af formlen, for at kunne beregne den fælles fordeling skal vi have de betingede sandsynligheder angivet af netværket. Men yderligere, at hvis vi har den fælles fordeling, så kan vi begynde at stille interessante spørgsmål. I det første eksempel spørger vi f.eks. om sandsynligheden for “REGN”, hvis “SEASON” er “WINTER”, og “DOG BARK” er “TRUE”.
Python eksempel på Belief Network
Så, jeg tror det er nok for teori og lad os se nogle rigtige eksempler med mit nuværende favorit programmeringssprog Python ❤️ Før du fortsætter, kan du finde Jupyter Notebook jeg har skrevet her.
# create the nodes
season = BbnNode(Variable(0, 'season', ), )
atmos_pres = BbnNode(Variable(1, 'atmos_press', ), )
allergies = BbnNode(Variable(2, 'allergies', ), )
rain = BbnNode(Variable(3, 'rain', ), )
grass = BbnNode(Variable(4, 'grass', ), )
umbrellas = BbnNode(Variable(5, 'umbrellas', ), )
dog_bark = BbnNode(Variable(6, 'dog_bark', ), )
cat_mood = BbnNode(Variable(7, 'cat_mood', ), )
cat_hide = BbnNode(Variable(8, 'cat_hide', ), )bbn = Bbn() \
.add_node(season) \
.add_node(atmos_pres) \
.add_node(allergies) \
.add_node(rain) \
.add_node(grass) \
.add_node(umbrellas) \
.add_node(dog_bark) \
.add_node(cat_mood) \
.add_node(cat_hide) \
.add_edge(Edge(season, allergies, EdgeType.DIRECTED)) \
.add_edge(Edge(season, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(season, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(atmos_pres, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, grass, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, dog_bark, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, cat_mood, EdgeType.DIRECTED)) \
.add_edge(Edge(dog_bark, cat_hide, EdgeType.DIRECTED)) \
.add_edge(Edge(cat_mood, cat_hide, EdgeType.DIRECTED))
Vi har først beskrevet vores knudepunkter med betingede sandsynligheder. Du skal bemærke, at jeg har sprunget nogle mulige tilstandsværdier over for enkelhedens skyld. For eksempel kan sæsonvariablen tage andre værdier “forår” og “efterår”. Så ideen er den samme.
Nu skal vi kontrollere, om vores netværk er konstrueret korrekt eller ej.
with warnings.catch_warnings():
warnings.simplefilter('ignore')
graph = convert_for_drawing(bbn)
pos = nx.nx_agraph.graphviz_layout(graph, prog='neato')plt.figure(figsize=(20, 10))
plt.subplot(121)
labels = dict()
nx.draw(graph, pos=pos, with_labels=True, labels=labels)
plt.title('BBN DAG')
Dette kodestykke ville resultere i følgende graf
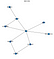
Så du kan se, at dette netværk passer med min fantasifulde tegning i begyndelsen. Lad os nu lave noget inferens på dette Belief Network.
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()join_tree.set_observation(ev)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
Dette kodestykke giver grundlæggende beviser til netværket, som er, at sæsonen er vinter med 1,0 sandsynlighed. I henhold til dette bevis får vi følgende resultater, når vi foretager inferencen.
0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.80000
3=sunny|0.20000
--------------------->
4|grass|grass,no_grass
4=grass|0.70000
4=no_grass|0.30000
--------------------->
1|atmos_press|high,low
1=high|0.50000
1=low|0.50000
--------------------->
5|umbrellas|on,off
5=on|0.95200
5=off|0.04800
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.66000
6=not_bark|0.34000
--------------------->
7|cat_mood|good,bad
7=good|0.23000
7=bad|0.77000
--------------------->
8|cat_hide|hide,show
8=hide|0.87150
8=show|0.12850
--------------------->
Når vi tilføjer yderligere beviser, f.eks. at hunden ikke gøer
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()ev2 = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('dog_bark')) \
.with_evidence('not_bark', 1.0) \
.build()join_tree.set_observation(ev)
join_tree.set_observation(ev2)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
får vi følgende inferenceresultater
0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.47059
3=sunny|0.52941
--------------------->
4|grass|grass,no_grass
4=grass|0.53529
4=no_grass|0.46471
--------------------->
1|atmos_press|high,low
1=high|0.39706
1=low|0.60294
--------------------->
5|umbrellas|on,off
5=on|0.88941
5=off|0.11059
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.00000
6=not_bark|1.00000
--------------------->
7|cat_mood|good,bad
7=good|0.52647
7=bad|0.47353
--------------------->
8|cat_hide|hide,show
8=hide|0.83162
8=show|0.16838
--------------------->
Ser du forskellen? 😆 Mange sandsynlighedsværdier ændres, når vi tilføjer beviserne i forbindelse med gøen. Det er helt sikkert et fjollet eksempel, men det er rart at få en intuition.
Hvordan bruger man Bayesianske netværk i SNA?
Bayesianske netværk er meget kraftfulde værktøjer til at forstå strukturen af kausalitetsrelationer mellem variabler. Når du har designet din model, kan den, selv med et lille datasæt, fortælle dig forskellige ting. Spørgsmålet i denne del er, hvordan man kan få gavn af Bayesian Nets i SNA. Svaret er ikke entydigt, men lad os starte med en dybtgående idé. I SNA forsøger vi at forstå strukturen i et socialt netværk. Desuden forsøger vi at forstå betydningen af knuderne. Men vi ved ikke, hvad resultaterne er af vores betydningsmålinger. Dette er det punkt, hvor Bayesian Networks finder sted. Hvis man f.eks. mener, at betydningen af en knude skyldes Degree Centrality og Link Centrality, kan man have følgende netværk:
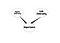
Dette er et meget naivt Bayesiansk netværk. Ud over at bestemme knudernes betydning kan yderligere anvendelse være at søge efter nogle bestemte typer knuder. Lad os overveje et socialt netværk, hvor der er nogle personer, som er potentielle ledere, og jeg ønsker at søge efter dem. Overvej følgende graf
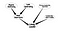
Dette lidt mere komplicerede netværk vil hjælpe os med at bestemme usikkerheden af de knuder, der er relateret til at være en leder.
En anden anvendelse vil være at udlede links. De nye links kan udledes af de eksisterende links. F.eks. kan der fra gruppemedlemskab i et socialt netværk udledes sandsynlige medlemskabslinks. Det, jeg mente, er, at vi kan modellere et nyt link mellem brugere og grupper ved at tage hensyn til eksisterende links. Se følgende modeldiagram
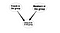
Så, dette er nogle grundlæggende eksempler på, hvordan Bayesian Networks kan anvendes i SNA. Dette emne er ikke undersøgt særlig godt, men jeg tror, at det kan være meget nyttigt at studere yderligere.
Slutning
Det svære ved Bayesian Networks er at designe. Især når man tænker på SNA, er det at konstruere kortlægning fra sociale netværk med et bayesiansk netværk kunst end videnskab 😃 Men når du først har gjort kunstarbejdet og designet din model meget godt, kan disse praktiske værktøjer fortælle dig en masse ting. Som vi ved, at Bayesian Networks anvendes på mange forskellige områder. Det fungerede meget godt i de fleste tilfælde. Derfor tror jeg stærkt på, at vi også kan drage meget dybtgående konklusioner på sociale netværk.
For yderligere undersøgelser med SNA og Bayesian Networks, stay tuned 🚀