Klassifikation er en overvåget maskinlæringsmetode, hvor algoritmen lærer af de data, den modtager, og derefter bruger denne læring til at klassificere nye observationer.
Med andre ord anvendes træningsdatasættet til at opnå bedre grænsebetingelser, som kan bruges til at bestemme hver målklasse; når sådanne grænsebetingelser er bestemt, er den næste opgave at forudsige målklassen.
Binære klassifikatorer arbejder kun med to klasser eller mulige resultater (eksempel: positiv eller negativ stemning; om långiver vil betale lånet eller ej; osv.), og flerklassede klassifikatorer arbejder med flere klasser (eksempel: hvilket land et flag tilhører, om et billede er et æble, en banan eller en appelsin; osv.) Multiclass antager, at hver prøve tildeles én og kun én etiket.

En af de første populære algoritmer til klassifikation inden for maskinlæring var Naive Bayes, en probabilistisk klassifikator inspireret af Bayes-teoremet (som giver os mulighed for at foretage begrundede slutninger om begivenheder, der sker i den virkelige verden, baseret på forudgående viden om observationer, der kan antyde det). Navnet (“Naive”) stammer fra det faktum, at algoritmen antager, at attributterne er betinget uafhængige.
Algoritmen er enkel algoritme at implementere og udgør normalt en fornuftig metode til at kickstarte klassifikationsbestræbelser. Den kan let skaleres til større datasæt (tager lineær tid i forhold til iterativ tilnærmelse, som anvendes til mange andre typer klassifikatorer, hvilket er dyrere i form af beregningsressourcer) og kræver en lille mængde træningsdata.
Naive Bayes kan imidlertid lide af et problem, der er kendt som ‘ nul-sandsynlighedsproblemet ‘, når den betingede sandsynlighed er nul for en bestemt attribut, hvilket ikke giver en gyldig forudsigelse. En løsning er at udnytte en udglatningsprocedure (f.eks. Laplace-metoden).

P(c|x) er den efterfølgende sandsynlighed for klasse (c, mål) givet prædiktor (x, attributter). P(c) er den forudgående sandsynlighed for klassen. P(x|c) er sandsynligheden, som er sandsynligheden for prædiktor givet klasse, og P(x) er den forudgående sandsynlighed for prædiktor.
Første trin i algoritmen handler om at beregne den forudgående sandsynlighed for givne klasseetiketter. Derefter finder man sandsynligheden for sandsynlighed med hver egenskab for hver klasse. Efterfølgende sættes disse værdier i Bayes-formlen & beregning af den efterfølgende sandsynlighed, og derefter ser man, hvilken klasse der har en højere sandsynlighed, givet at input tilhører den klasse med højere sandsynlighed.
Det er ret ligetil at implementere Naive Bayes i Python ved at udnytte scikit-learn-biblioteket. Der er faktisk tre typer Naive Bayes-modeller under scikit-learn-biblioteket: (a) Gaussisk type (antager, at funktionerne følger en klokkelignende normalfordeling), (b) Multinomial (anvendes til diskrete tællinger i form af antal gange, et resultat observeres på tværs af x forsøg) og (c) Bernoulli (nyttig til binære funktionsvektorer; populært anvendelsestilfælde er tekstklassificering).
En anden populær mekanisme er beslutningstræet. Gives en data af attributter sammen med dens klasser, producerer træet en sekvens af regler, der kan bruges til at klassificere dataene. Algoritmen opdeler prøven i to eller flere homogene sæt (blade) på grundlag af de mest betydningsfulde differentiatorer i dine inputvariabler. For at vælge en differentiator (prædiktor) overvejer algoritmen alle funktioner og foretager en binær opdeling af dem (for kategoriske data opdeles efter kat; for kontinuerlige data vælges en cut-off tærskelværdi). Den vælger derefter den med de mindste omkostninger (dvs. højeste nøjagtighed) og gentager rekursivt, indtil det lykkes at opdele dataene i alle blade (eller når den maksimale dybde).
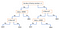
Decision Trees er generelt enkle at forstå og visualisere og kræver kun lidt datapræparering. Denne metode kan også håndtere både numeriske og kategoriske data. På den anden side generaliserer komplekse træer ikke godt (“overfitting”), og beslutningstræer kan være noget ustabile, fordi små variationer i dataene kan resultere i, at der genereres et helt andet træ.
En metode til klassificering, der er afledt af beslutningstræer, er Random Forest, som i det væsentlige er en “meta-estimator”, der tilpasser et antal beslutningstræer på forskellige delprøver af datasæt og bruger gennemsnittet til at forbedre modellens forudsigelsesnøjagtighed og kontrollere overfitting. Delprøvestørrelsen er den samme som den oprindelige inputprøve – men prøverne trækkes med udskiftning.
Random Forests har tendens til at udvise en højere grad af robusthed over for overfitting (>robusthed over for støj i data), med en effektiv udførelsestid selv i større datasæt. De er dog mere følsomme over for ubalancerede datasæt, men er også en smule mere komplekse at fortolke og kræver flere beregningsressourcer.
En anden populær klassifikator i ML er logistisk regression – hvor sandsynligheder, der beskriver de mulige udfald af et enkelt forsøg, modelleres ved hjælp af en logistisk funktion (klassifikationsmetode trods navnet):

Her er, hvordan den logistiske ligning ser ud:
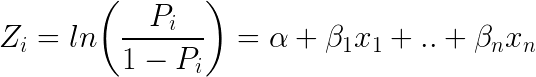
Tager man e (eksponent) på begge sider af ligningen, får man:
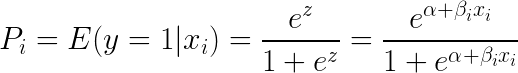
Logistisk regression er mest nyttig til at forstå indflydelsen af flere uafhængige variabler på en enkelt udfaldsvariabel. Den er fokuseret på binær klassifikation (til problemer med flere klasser bruger vi udvidelser af logistisk regression som f.eks. multinomial og ordinær logistisk regression). Logistisk regression er populær på tværs af use-cases såsom kreditanalyse og tilbøjelighed til at reagere/købe.
Sidst men ikke mindst anvendes kNN (for “k Nearest Neighbors”) også ofte til klassifikationsproblemer. kNN er en simpel algoritme, der gemmer alle tilgængelige tilfælde og klassificerer nye tilfælde på grundlag af et lighedsmål (f.eks. afstandsfunktioner). Den er blevet anvendt inden for statistisk estimering og mønstergenkendelse allerede i begyndelsen af 1970’erne som en ikke-parametrisk teknik:

