(IUCr) Symboler for symmetrielementer

Acta Cryst. (1992). A48, 727-732

Slutrapport fra International Union of Crystallography Ad-Hoc Committee on the nomenclature of symmetry*

Af P. M. DE WOLFF (formand), Meermanstraat 126, 2614 AM Delft, Nederlandene,

Y. BILLIET, Ecole Nationale d’Ingénieurs, BPW 3038 Sfax, Tunesien,

J. D. H. DONNAY, Department of Geological Sciences, McGill University, 3450 University Street, Montreal, Canada H3A 2A7,

W. FISCHER, Institut für Mineralogie, Petrologie und Kristallographie der Phillips-Universität, Lahnberge, D-3550 Marburg (Lahn), Tyskland,

R. B. GALIULIN, Institute of Crystallography, Academy of Sciences of Russia, Leninsky Prospekt 59, Moscow 117333, Rusland,

A. M. GLAZER, Clarendon Laboratory, University of Oxford, Parks Road, Oxford OX1 3PU, England,

TH. HAHN, Institut für Kristallographie, RWTH, Templergraben 55, D-5100 Aachen, Tyskland,

MARJORIE SENECHAL, Department of Mathematics, Smith College, Northampton, MA 01063, USA,

D. P. SHOEMAKER, Kemiafdelingen, Oregon State University, OR 97331, USA,

H. WONDRATSCHEK, Institut für Kristallographie, Universität Karlsruhe, Kaiserstrasse 12, D-7500 Karlsruhe 1, Tyskland,

A. J. C. WILSON (ex officio, IUCr Commission on International Tables), Crystallographic Data Centre, University Chemistry Laboratory, Lensfield Road, Cambridge CB2 1EW, England

OG S. C. ABRAHAMS (ex officio, IUCr Commission on Crystallographic Nomenclature), Department of Physics, Southern Oregon State College, 1250 Siskiyou Boulevard, Ashland, OR 97520-5047, USA

(Modtaget den 7. november 1991; accepteret den 9. marts 1992)

* Udpeget den 14. november 1984, ændret den 10. august 1987 i henhold til de regler, der er beskrevet i Acta Cryst. (1979), A35, 1072. Endelig rapport accepteret 23. december 1991 af IUCr Commission on Crystallographic Nomenclature og 9. marts 1992 af Executive Committee.

Abstract

Nye eller omdefinerede trykte symboler foreslås i lyset af den nyligt accepterede omdefinition af symmetrielementer . Især bogstavet e dækker visse glideplaner, som hidtil ikke har haft et entydigt symbol, f.eks. dem, der kaldes “enten a eller b”. Det anbefales at anvende e i Hermann-Mauguin-symbolet for fem forskellige rumgrupper. For e-fly, der projiceres i en retning parallelt med planen, foreslås et grafisk symbol, som fjerner den tvetydighed, der er forbundet med deres nuværende betegnelse. Bogstavet k foreslås for en nydefineret klasse af glideplaner, som hidtil har været uden specifikt symbol. De symboler for symmetrioperationer, der er indført i rumgruppebeskrivelserne i International Tables for Crystallography (1989), Vol. A (Dordrecht: Kluwer Academic Publishers), anbefales til generel brug, med ændringer kun for glidreflektionsoperationer.

Indledning

Den ad hoc-komité, der blev nedsat i 1980 for at overveje “nomenklaturproblemer vedrørende symmetrioperationer og symmetrielementer i rumgrupper”, har udgivet to rapporter med titlen Nomenklatur for krystalfamilier, Bravais-Lattice-typer og aritmetiske klasser (de Wolff et al, 1985) og “Definition of Symmetry Elements in Space Groups and Point Groups” (de Wolff et al., 1989). Som nævnt i 1989-rapporten er det eneste udestående problem vedrørende symmetrioperationer at vælge passende symboler, da begrebet er klart. En foreløbig notation er blevet vedtaget i International Tables for Crystallography (1983, 1989), i det følgende benævnt ITA83.

Trykte symboler for symmetrielementer

Den definition af symmetrielementer, som den er givet i 1989-rapporten (de Wolff et al.), vil blive anvendt i hele denne rapport. Her gentages det væsentligste:

For enhver given symmetrioperation defineres dens geometriske element (plan, punkt og/eller linje). Et symmetrielement er kombinationen af det geometriske element for en af symmetrioperationerne i en given rumgruppe med mængden (kaldet `elementmængden’) af alle symmetrioperationer i denne rumgruppe, som deler dette geometriske element.

Eksplicitte definitioner af geometriske elementer og beskrivelser af de deraf følgende symmetrielementer samt deres symboler findes i tabel 1 og 2. (Disse er identiske med tabel 1 og 2 i 1989-rapporten undtagen for glideplaner og gentages her for fuldstændighedens skyld, se nedenfor). Hvert symmetrielement er repræsenteret ved et symbol bestående af to tegn. Det første tegn er et E med store bogstaver for alle symmetrielementer. Det tjener til at vise, at symbolet henviser til et symmetrielement og ikke f.eks. til en symmetrioperation. Hvis dette allerede fremgår klart af sammenhængen, kan E’et udelades, f.eks. “en akse 2” i stedet for “en akse E2”.

Tabel 1. Geometriske elementer for symmetrioperationer i punktgrupper og rumgrupper
Symmetrioperation	Geometrisk element	Supplerende parametre
Identitet	Ikke påkrævet	Ingen
Translation	Ikke påkrævet	Vektor $\mathbf{t}$
Refleksion i plan A	Plan A	Ingen
Glide refleksion = refleksion i plan A og translation $\mathbf{v}$ parallel til A	Plan A	Glidvektor $\mathbf{v}$
Rotation om linie b	Linie b	Vinkel og rotationsretning
Skrue rotation = rotation om linie b og translation $\mathbf{u}$ parallel til b	Linie b	Vinkel og retning af rotationsskruevektor $\mathbf{u}$
Rotoinversion = rotation om linje b og inversion gennem punkt P på b	Linje b og punkt P på b	Vinkel (ikke lig med $\pi$ ) og rotationsretning
Inversion gennem punkt P	Punkt P	Punkt P	Ingen

Symbolet Eg, der er anført i 1989-rapporten, kan anvendes for glideplaner, hvis man blot ønsker at vise, at symmetrielementet er et glideplan. Hvis det derimod hører til en af de specielle typer, som længe har været betegnet med et passende bogstav (a, b, c, n eller d; jf. ITA83), så erstatter dette bogstav g i Eg.

Tabel 2. Symmetrielementer i punktgrupper og rumgrupper
Navn på symmetrielement	Symbol	Geometrisk element	Definerende operation (d.o.)	Operationer i elementmængden
Spejlplan	Em	Plan A	Refleksion i A	D.o. og dens koplanære ækvivalenter*
Glidplan	Eg $\ddag$	Plan A	Glidspejling i A, 2v (ikke v) en gittertranslation	D.o. og dens koplanære ækvivalenter*
Rotationsakse	En	Linje b	Rotation om b, vinkel $2\pi/n$ ,n = 2, 3, 4 eller 6	1., $\dots$ ,(n – 1)th powers of d.o. og deres koaksiale ækvivalenter\dag
Skrueakse	Enj	Linje b	Skrue rotation om b, vinkel $2\pi/n$ , u =j/n gange korteste gitter translation langs b, højre skrue; n = 2, 3, 4 eller 6, $j=1,\dots,(n-1)$	1st, $\dots$ ,(n – 1)th potenser af d.o. og deres koaksiale ækvivalenter\dag
Rotoinversionsakse	$E\bar n$	Linje b og punkt P på b	Rotoinversion: rotation om b, vinkel $2\pi/n$ , og inversion gennem P; n = 3, 4 eller 6	D.o. og dens invers
Center	$E\bar 1$	Punkt P	Invertering gennem P	D.o. kun

* Det vil sige alle glidereflektioner med samme refleksionsplan, med glidevektorer, der adskiller sig fra d.o. (som for en refleksion antages at være nul) med en gittertranslationsvektor.
\dag Det vil sige alle rotationer og skrue-rotationer med samme akse b, samme vinkel og rotationsretning og samme skruevektor $\mathbf{u}$ (nul for en rotation) op til en gittertranslationsvektor.
$\ddag$ I Eg erstattes g af a, b, c, n, d, e eller k for bestemte typer af glideplaner, jf. §2.

Et vigtigt nyt aspekt ved symboler som Eb kan dog påpeges. Ifølge ITA83 betød betegnelsen af et plan med b blot, at en gliderefleksion i planen med en glidekomponent b/2 langs b-aksen er en symmetrioperation. Denne definition gælder helt sikkert for den situation, der er afbildet i fig. 1.

Fig. 1. (Efter W. Fischer.) Elementmængden af et Eb-glideplan, vist som en række punkter over (+) og under (-) det plan, der fremkommer ved glidereflektioner i planen, f.eks. med udgangspunkt i +-tegnet øverst til venstre. Netto N af translationer parallelt med planen (+$\cdots$ +-vektorer) er angivet med en maske, som i dette tilfælde tilfældigvis er rektangulær. Begge par af kanter er parallelle med krystalakserne. Der er en gliderefleksion med dens glidevektor (+ $\cdots$ -) langs b-aksen.

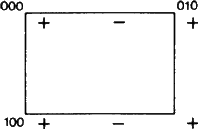
$\begin{figure} \includegraphics {fig1.ps} \end{figure}$

Figur 1 er ligesom figur 2 og 3 tilpasset fra et sæt lignende figurer, der er udarbejdet af ad hoc-udvalgsmedlem W. Fischer som en fortegnelse over alle typer glideplaner. Selv om sættet blev forelagt udvalget i 1980, længe før 1989-rapporten udkom, viser hver af figurerne nøjagtigt “elementsættet” af svæveflyet som defineret i denne rapport (jf. ovenstående resumé). For et glideplan består elementmængden af alle glidereflektioner, der har planen som deres fælles geometriske element. Deres virkning er vist i projektion på dette plan. Fra startpositionen for ethvert +-tegn er hvert -tegn et resultat af en af glidereflektionerne i mængden. Alle disse er vist inden for et elementært net af det resulterende todimensionale periodiske mønster af + og – tegn.

Vi vil ofte henvise til nettet N dannet af alle translationer parallelt med planen; dette net er let at visualisere ved kun at se på + tegn. Disse vektorer skal skelnes skarpt fra de vektorer, der forbinder et +-tegn med et hvilket som helst -tegn, som hver især er glidevektor for en gliderefleks, der tilhører elementmængden.

Det nye aspekt opstår, fordi b-glideplanet i nogle tilfælde, ifølge ITA83-definitionen, også er et a-glideplan; se fig. 2. Det er klart, at dette kun sker, hvis nettet N er ortogonalt centreret, for så kan a-glidet ændres til et b-glid (og omvendt) ved at tilføje en centrerende translation. Hidtil har praksis været at kalde et sådant glideplan vilkårligt enten a eller b, hvilket har medført en uberettiget skævhed og en manglende entydighed i disse symboler. Vi foreslår derfor, at tilfældet i fig. 2 dækkes af et særskilt symbol.

Fig. 2. (Efter W. Fischer.) Elementmængden af et Ee-glideplan. Jf. billedtekst til fig. 1. Bemærk, at nettet N her er ortogonalt centreret.

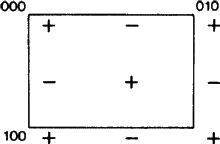
$\begin{figure} \includegraphics {fig2.ps} \end{figure}$

Symbolets anvendelsesområde bør derefter udvides til at omfatte glideplaner i diagonal orientering, dvs. parallelle med blot én krystalakse, forudsat at glideplanen har en glidevektor langs denne akse, og at nettet N er ortogonalt centreret. For sådanne planer er der ikke den samme tvetydighed som i ovenstående a-b tilfældige valg, men det nye symbols udvidede anvendelsesområde er på linje med anvendelsesområdet for alle eksisterende symboler (nemlig a, b, c, n og d). Hver af disse anvendes for et glideplan med både én og to krystalakser i nettet N, jf. fig. 3.

Bogstavet e foreslås til det nye symbol. Ee vil således gælde for glideplaner med ortogonale centrerede net N og mindst én glidevektor langs en krystalakse. Det er derfor nødvendigt med et nyt kriterium: nemlig glidevektorernes orientering i forhold til krystallens konventionelle akser. Da sidstnævnte er langs symmetrieretninger, mens hvert glideplan er parallelt med et spejlplan i gitteret, er det ikke overraskende, at der altid er mindst én konventionel krystalakse i N. Hvis der kun er én sådan akse, er der altid en anden translation i N vinkelret på denne akse.

Det nye symbol e samt de gamle symboler a, b, c, d, n vil nu blive omdefineret ud fra dette nye kriterium og ud fra Bravais-nettets type N. Dette net er monoklin eller ortogonalt eller tetragonalt primitivt (mp eller op eller tp) eller ortogonalt centreret (oc). Kun net N af oc-typen tillader et Ee-glideplan. Symbolet En gælder for net N af Bravais-typen mp eller op, mens Ed gælder for net N af oc-typen. (Som anført i en fodnote til tabel 1.3 i ITA83: “Glideplaner d forekommer kun i orthorhombiske F-rumgrupper, i tetragonale I-rumgrupper og i kubiske I- og F-rumgrupper. De forekommer altid parvis med vekslende glidevektorer”). I modsætning til Ea-, Eb-, Ec- og Ee-planerne findes der imidlertid for En- og Ed-planerne ingen glidevektor hverken parallelt eller vinkelret på en konventionel akse i N.

De efterfølgende definitioner af glideplanerne af de ovennævnte typer er opsummeret i linierne (i) og (ii) i tabel 3 og mere eksplicit i fig. 3.

Tabel 3. Udtrykte symboler for særlige typer af glideplaner
Antal glidevektorer parallelt eller vinkelret på krystalakserne i net N	Bravais-type af net N
Symbolet bestemmes ud fra to kriterier. Det ene kriterium er Bravais-typen (mp, op, tp eller oc) af det net N, der dannes af de symmetriske translationer parallelt med det pågældende plan. Dette net indeholder altid mindst én konventionel krystalakse.* Det andet kriterium henviser til glidevektorernes orientering i forhold til disse akser.
	m, op, tp	oc
(i) En eller to parallelle	Ec(Ea, Eb)	Ee
(ii) Ingen parallelle, ingen vinkelrette	En	Ed
(iii) Ingen parallelle, en vinkelret	Ek	–

* Som defineret i ITA83, § 9.1; for rhomboedriske rumgrupper anvendes her dog kun hexagonale akser.

Alle resterende glidefly var tidligere uden specifikt symbol. De har hver især en diagonal orientering (kun én konventionel krystalakse i netto N). Blandt glidereflektionerne i deres elementmængde er der ingen med en glidevektor langs denne akse. En glidevektor er dog (ved symmetri) vinkelret på den. Det nye symbol Ek er kort defineret i linje (iii) i tabel 3 og er fuldt ud illustreret i den nederste blok i fig. 3. Der er givet nogle eksempler i § 2.

Fig. 3. (Tilpasset efter W. Fisher’s tegninger.) Alle mulige aspekter af elementmængderne af glideplanerne vist som i fig. 1, men uafhængigt af aksebetegnelser. Diagrammerne er grupperet i kolonner med overskrift af Bravais-net-symbolet (øverste linje) for deres net N, jf. tabel 3. De øvrige kriterier i denne tabel kontrolleres ved først at se på de dobbelte linjer, der viser retningerne af krystalakserne i planen. En kant (lodret) af det viste net N er altid valgt langs en sådan akse. Den anden kant er vandret, undtagen i (1) og (8). For diagrammerne (1), $\dots$ ,(5) er symbolet for glideplanet betegnelsen a, b eller c for den lodrette akse; for de øvrige er det det omkransede bogstav i den omskrevne blok, der indeholder diagrammet. Bemærk de lodrette glidevektorer i diagrammerne (1), $\dots$ ,(7), de vandrette i (6), (7), (14), (15) og fraværet af nogen af dem i (8), $\dots$ ,(13). Et eksempel på forekomsten er angivet under hvert diagram med rumgruppesymbolet og planets koordinattriplet.

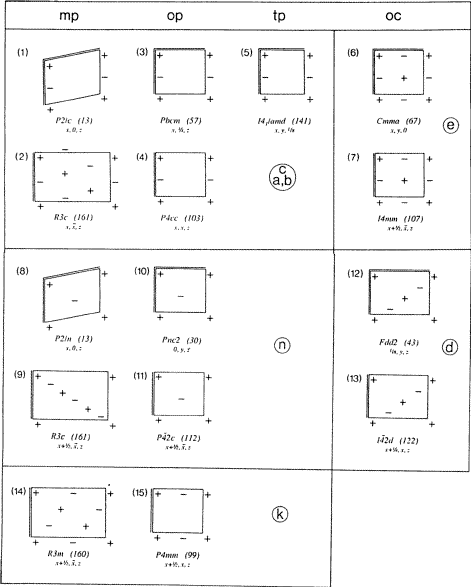
$\begin{figure} \includegraphics {fig3.ps} \end{figure}$

I fig. 3 er Fischers opgørelse over alle typer af glideplaner vist på en forkortet – om end stadig komplet – måde, hvor krystalakserne har fået mere grafisk vægt. For hvert diagram er der anført et eksempel på dets forekomst i en rumgruppe.

I nogle rhomboedriske rumgrupper forekommer diagonalt orienterede Ec-, En- og Ek-planer med mp-type net N, som kan beskrives ved tredobbelt centrering af et ortogonalt net. En rektangulær tredobbelt maske af nettet N er vist for disse typer af glideplaner i fig. 3, diagrammer (2), (9) og (14). I diagram (9) erkendes ligheden med andre n-diagrammer som f.eks. (8) eller (10), hvis man i (9) betragter en monoklin primitiv maske af net N med diagonale glidevektorer.

Grafiske symboler for symmetrielementer

De eksisterende grafiske symboler som defineret og anvendt i ITA83 anses af ad hoc-udvalget for at være tilstrækkelige med én undtagelse. Situationen er meget forskellig fra situationen for trykte symboler, fordi projektionsretningen i tegninger bliver en ekstra parameter. I udtrykkene “vinkelret projektion” og “parallel projektion”, der anvendes nedenfor, henviser vinkelret og parallel til projektionsretningens orientering i forhold til glideplanet.

For et Ee-plan findes symbolet 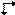for dets vinkelrette projektion. De eksisterende grafiske symboler for den parallelle projektion af et Ee-glideplan lider imidlertid af den samme tvetydighed som de trykte symboler. De udtrykker glidevektoren enten parallelt eller vinkelret på projektionsretningen, men valget er arbitrært. Der foreslås derfor et nyt symbol for parallelprojektionen af et Ee-glideplan, nemlig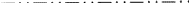

Eksempler på Ee-planer.

Alle glideplaner parallelle med to akser i rumgrupperne Fmm2, Fmmm, $Fm\bar 3$ , $Fm\bar 3m$ og $Fm\bar 3c$ (nr. 42, 69, 202, 225 og 226), samt visse planer i de fem rumgrupper, der er nævnt i §3.

Diagonalt orienterede Ee-planer forekommer i rumgrupperne I4mm, I4cm, $I\bar 42m$ , I4/mmm, I4/mcm, $I\bar 43m$ og $Im\bar 3m$ (nr. 107, 108, 121, 139, 140, 217 og 229).

I ITA83 er alle disse Ee-planer tegnet ret arbitrært som enten stiplede eller stiplede linjer i deres parallelle projektioner. Fig. 4 viser diagrammet for rumgruppe I4cm (nr. 108), både som det er vist i ITA83 og med brug af det nye symbol.

Fig. 4. (a) Diagram over rumgruppe I4cm (nr. 108) taget fra ITA83. (b) Samme, modificeret ved anvendelse af det grafiske symbol, der er foreslået i § 2, for parallelprojektionen af et Ee-plan.

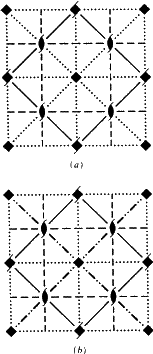
$\begin{figure} \includegraphics {fig4.ps} \end{figure}$

Selv om Ek er et nyt tryksymbol, er alle glideplaner Ek i diagrammerne i ITA83 blevet tegnet tilfredsstillende med de samme konventioner som dem, der anvendes for Ea/b/c glideplaner. Som i disse tilfælde er der en enkelt speciel glidevektor (vinkelret på krystalaksen i net N, jf. tabel 3). Når denne vektor f.eks. er parallel med projektionsplanet, er Ek-planet altid tegnet som den stiplede linje, der er foreskrevet i den relevante konvention. Der foreslås derfor ikke noget nyt grafisk symbol for Ek-glideplaner.

Eksempler på Ek-planer.

Sådanne planer findes let i diagrammerne i ITA83 som planer parallelle med blot én akse og projiceret som stiplede linjer, f.eks. xxz i P4bm og $P\bar 42_1m$ (nr. 100 og 113). Navnlig er tabel 3 nøjagtigt i overensstemmelse med den viste sondring mellem Ek- og En-planerne. Se f.eks. de stiplede og stiplede linjer for R3m og R3c (nr. 160 og 161).

Hermann-Mauguin-rumgruppesymboler

De tegn, der optræder efter gitterbogstavet i Hermann-Mauguin-symbolet (HM) for en rumgruppe, var oprindeligt beregnet til at repræsentere genererende operationer af gruppen. F.eks. var b en b-glidende refleksion i et plan orienteret efter dets position i HM-symbolet.

I praksis tog de populære omend dårligt definerede symmetrielementer over for operationerne. Således kom b til at blive betragtet som et glideplan, Eb i vores nuværende terminologi. Der er ingen skade i denne nyfortolkning, undtagen når operationen hører til et Ee-glideplan. Hvis dette f.eks. gælder for ovenstående b-gliderefleksion, findes der et Ee-, men ikke et Eb-glideplan i den tilsvarende orientering. I dette tilfælde bliver b en meget misvisende karakter. Bortset fra dette er den skævhed (der gives til b frem for a eller c) lige så forstyrrende som i tilfældet med de symmetrielement-symboler, der behandles i §1.

Der foreslås derfor at erstatte sådanne vildledende bogstaver a eller b med e i alle de fem HM-symboler, hvor de forekommer:

Rumgruppe nr.	39	41	64	67	68
Symbol i ITA83:	Abm2	Aba2	Cmca	Cmma	Ccca
Nyt symbol:	Aem2	Aea2	Cmce	Cmce	Cmme	Ccce.

En yderligere fordel ved de foreslåede nye symboler er, at e – i modsætning til a eller b – er neutralt og derfor ikke ændres ved permutation af akserne.

Trykte symboler for symmetrioperationer

Et komplet sæt tryksymboler blev designet af W. Fischer & E. Koch (ITA83, §11.2) og blev i vid udstrækning anvendt i afsnittene om symmetrioperationer i rumgruppebeskrivelserne.

Kort fortalt består hvert symbol af op til tre dele. Den første del er et enkelt tegn (nogle gange med et indeks), som beskriver den slags operation. Den/de følgende del(e) angiver komponenterne af en eventuel relevant forskydnings- eller translationsvektor – altid i parentes – og koordinaterne for operationens geometriske element, i den rækkefølge.

Ad hoc-udvalget ønsker efter at have overvejet dette system at indføre to ændringer for glidereflektioner:

(i) i stedet for det nuværende første tegn (som kan være a, b, c, n, d eller g), skal man altid skrive bogstavet g;

(ii) altid skrive glidevektorens komponenter (i parentes) fuldt ud, især for de simple glidereflektioner i a-, b- eller c-glideplaner, hvor de tidligere blev udeladt.

Regel (i) undertrykker oplysninger om den type glideplan, som operationen hører til. Meget ofte er disse oplysninger irrelevante eller endog forvirrende. For a/b/c-planer kan undertrykkelsen ødelægge væsentlige oplysninger, men tabet genoprettes af regel (ii) som vist i eksemplet nedenfor.

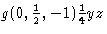Med disse ændringer forbedres symbolernes ensartethed – også med hensyn til dem for rotationer – betydeligt. F.eks. falder symbolet for gliderefleksionen i planen $x = \frac{1}{4}$ , med den usædvanlige glidevektor $(0, \frac{1}{2}{2}, -1)$ , nemlig $g(0, \frac{1}{2}, 1) \frac{1}{4}yz$ , nu på linje med symbolet for en simpel b-gliderefleksion. I ITA83 blev sidstnævnte betegnet med $b \frac{1}{4} y z$ , men dette ændres ved regel (ii) til $g(0, \frac{1}{2}, 0) \frac{1}{4} y z$ .

Overstående regler gælder også for glidereflektioner, der hører til elementmængden i et spejlplan. Hvis forskydningskomponenten af en sådan operation således er (0, 1, 2), begynder dens symbol med g(0, 1, 2), ikke med m(0, 1,2).

International Tables for Crystallography (1983). Vol. A, redigeret af TH. HAHN, især §§ 1.1, 1.3, 1.4, 7 og 11. Dordrecht: Kluwer Academic Publishers.

International Tables for Crystallography (1989). Vol. A, 2., reviderede, 2. udgave, redigeret af TH. HAHN. Dordrecht: Kluwer Academic Publishers.

WOLFF, P. M. DE, BELOV, N. V., BERTAUT, E. F., BUERGER, M. J., DONNAY, J. D. H., FISCHER, W., HAHN, TH., KOPTSIK, V. A. A., MACKAY, A. L., WONDRATSCHEK, H., WILSON, A. J. C. & ABRAHAMS, S. C. (1985). Acta Cryst. A41, 278-280.

WOLFF, P. M. DE, BILLIET, Y., DONNAY, J. D. H., FISCHER, W., GALIULIN, R. B., GLAZER, A. M., SENECHAL, M., SHOEMAKER, D. P., WONDRATSCHEK, H., HAHN, TH., WILSON, A. J. C. & ABRAHAMS, S. C. (1989). Acta Cryst. A45, 494-499.

…vektorer. Glideplansymbolerne c, n og k for de tre diagrammer (2), (9) og (14) i fig. 3 er naturligvis blevet tildelt i henhold til tabel 3. Et medlem af ad hoc-udvalget (professor Wondratschek) mener, at symbolet n for diagram (9) er i modstrid med traditionelle opfattelser af n planer. Han foreslår, at der tilknyttes et særligt symbol til diagram (9). Dette forslag har dog ikke fået tilstrækkelig støtte i Ad-hoc-udvalget.

Symboler for symmetrielementer og symmetrioperationer