En este artículo, explicaré cómo se implementan las convoluciones 2D como multiplicaciones matriciales. Esta explicación está basada en los apuntes del CS231n Redes Neuronales Convolucionales para el Reconocimiento Visual (Módulo 2). Asumo que el lector está familiarizado con el concepto de una operación de convolución en el contexto de una red neuronal profunda. Si no es así, este repo tiene un informe y excelentes animaciones que explican qué son las convoluciones. El código para reproducir los cálculos de este artículo se puede descargar aquí.

Pequeño ejemplo

Supongamos que tenemos una imagen de un solo canal 4 x 4, X, y sus valores de píxel son los siguientes:

Supongamos además que definimos una convolución 2D con las siguientes propiedades:

Propiedades de la operación de convolución 2D que queremos realizar sobre nuestra imagen

Esto significa que habrá 9 parches de imagen de 2 x 2 que serán multiplicados elemento a elemento con la matriz W, así:

Todos los posibles parches de imagen 2 x 2 en X dados los parámetros de la convolución 2D. Cada color representa un parche único

Estos parches de imagen pueden representarse como vectores columna de 4 dimensiones y concatenarse para formar una única matriz de 4 x 9, P, así:

Nótese que la i-ésima columna de la matriz P es en realidad el i-ésimo parche de imagen en forma de vector columna.

La matriz de pesos para la capa de convolución, W, se puede aplanar a un vector de filas de 4 dimensiones , K, así:

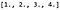
Para realizar la convolución, primero multiplicamos matricialmente K con P para obtener un vector de filas de 9 dimensiones (matriz 1 x 9) que nos da:

Después remodelamos el resultado de K P a la forma correcta, que es una matriz de 3 x 3 x 1 (dimensión del canal por último). La dimensión del canal es 1 porque ponemos los filtros de salida a 1. La altura y la anchura es 3 porque según las notas del CS231n:

Esto significa que el resultado de la convolución es:

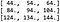
Lo cual se comprueba si realizamos la convolución usando las funciones incorporadas de PyTorch (ver el código que acompaña a este artículo para más detalles).

Ejemplo más grande

El ejemplo de la sección anterior asume una sola imagen y los canales de salida de la convolución son 1. Qué cambiaría si relajamos estos supuestos?

Supongamos que nuestra entrada a la convolución es una imagen de 4 x 4 con 3 canales con los siguientes valores de píxeles:

Valores de los píxeles en nuestra imagen de entrada de 4 x 4 x 3

En cuanto a nuestra convolución, la configuraremos para que tenga las mismas propiedades que en el apartado anterior, excepto que sus filtros de salida son 2. Esto significa que la matriz de pesos inicial, W, debe tener forma (2, 2, 2, 3) es decir (filtros de salida, altura del núcleo, anchura del núcleo, canales de la imagen de entrada). Vamos a configurar W para que tenga los siguientes valores

Nótese que cada filtro de salida tendrá su propio kernel (por eso tenemos 2 kernels en este ejemplo) y el canal de cada kernel es 3 (ya que la imagen de entrada tiene 3 canales).

Como todavía estamos convolucionando un kernel de 2 x 2 sobre una imagen de 4 x 4 con 0 zero-padding y stride 1, el número de parches de imagen sigue siendo 9. Sin embargo, la matriz de parches de imagen, P, será diferente. Más concretamente, la columna i-ésima de P será la concatenación de los valores de los canales primero, segundo y tercero (como vector de columna) correspondientes al parche de imagen i. P será ahora una matriz de 12 x 9. Las filas son 12 porque cada parche de imagen tiene 3 canales y cada canal tiene 4 elementos, ya que fijamos el tamaño del núcleo en 2 x 2. Este es el aspecto de P:

Al igual que para W, cada núcleo se aplanará en un vector de filas y se concatenará fila por fila para formar una matriz de 2 x 12, K. La fila i-ésima de K es la concatenación de los valores del primer, segundo y tercer canal (en forma de vector de fila) correspondientes al núcleo i-ésimo. Este es el aspecto que tendrá K:

Ahora sólo queda realizar la multiplicación matricial K P y darle la forma correcta. La forma correcta es una matriz de 3 x 3 x 2 (la última dimensión del canal). Aquí está el resultado de la multiplicación:

Y aquí está el resultado después de remodelarla a una matriz de 3 x 3 x 2:

Lo que de nuevo se comprueba si realizamos la convolución usando las funciones incorporadas de PyTorch (ver el código que acompaña a este artículo para más detalles).

¿Y qué?

¿Por qué deberíamos preocuparnos por expresar las convoluciones 2D en términos de multiplicaciones de matrices? Además de tener una implementación eficiente y adecuada para ejecutarse en una GPU, el conocimiento de este enfoque nos permitirá razonar sobre el comportamiento de una red neuronal convolucional profunda. Por ejemplo, He et. al. (2015) expresaron las convoluciones 2D en términos de multiplicaciones de matrices, lo que les permitió aplicar las propiedades de las matrices/vectores aleatorios para argumentar una mejor rutina de inicialización de pesos.

Conclusión

En este artículo, he explicado cómo realizar convoluciones 2D utilizando multiplicaciones de matrices recorriendo dos pequeños ejemplos. Espero que esto sea suficiente para que puedas generalizar a dimensiones de imagen de entrada y propiedades de convolución arbitrarias. Hazme saber en los comentarios si algo no está claro.

Convolución en 1D

El método descrito en este artículo se generaliza a las convoluciones en 1D también.

Por ejemplo, suponga que su entrada es un vector de 3 canales de 12 dimensiones como el siguiente:

Si configuramos nuestra convolución 1D para que tenga los siguientes parámetros:

• tamaño del núcleo: 1 x 4
• canales de salida: 2
• stride: 2
• padding: 0
• bias: 0

Entonces los parámetros en la operación de convolución, W, serán un tensor con forma (2 , 3, 1, 4). Establezcamos que W tiene los siguientes valores:

En base a los parámetros de la operación de convolución, la matriz de parches de «imagen» P, tendrá una forma (12, 5) (5 parches de imagen donde cada parche de imagen es un vector 12-D ya que un parche tiene 4 elementos a través de 3 canales) y se verá así:

Valores para P, una matriz de 12 x 5

A continuación, aplanamos W para obtener K, que tiene forma (2, 12) ya que hay 2 núcleos y cada núcleo tiene 12 elementos. Este es el aspecto de K:

Ahora podemos multiplicar K con P lo que da:

El resultado de K P, una matriz de 2 x 5

Por último, remodelamos el K P a la forma correcta, que según la fórmula es una «imagen» con forma (1, 5). Esto significa que el resultado de esta convolución es un tensor con forma (2, 1, 5), ya que hemos puesto los canales de salida a 2. Este es el resultado final:

Lo cual, como era de esperar, se comprueba si realizáramos la convolución utilizando las funciones incorporadas de PyTorch.