Posted on

Fase (ondas)

, Author

La fase de una oscilación u onda es la fracción de un ciclo completo que corresponde a un desplazamiento desde un punto de referencia especificado en el tiempo t = 0. La fase es un concepto del dominio de la frecuencia o de la transformada de Fourier, y como tal, puede entenderse fácilmente en términos de movimiento armónico simple. El mismo concepto se aplica al movimiento ondulatorio, visto ya sea en un punto del espacio durante un intervalo de tiempo o a través de un intervalo del espacio en un momento del tiempo. El movimiento armónico simple es un desplazamiento que varía cíclicamente, como se representa a continuación:

File:Simple harmonic motion.png

y descrito por la fórmula:

{displaystyle x(t)=A\cdot \sin(2\pi ft+\theta ),}

donde A es la amplitud de la oscilación, f es la frecuencia, t es el tiempo transcurrido, y {displaystyle \theta } es la fase de la oscilación. La fase determina o está determinada por el desplazamiento inicial en el tiempo t = 0. Un movimiento con frecuencia f tiene periodo {displaystyle T={frac {1}{f}}.}

Pueden observarse dos posibles ambigüedades:

  • Una es que el desplazamiento inicial de {displaystyle \cos(2\pi ft+\theta )},} es diferente al de la función seno, aunque parecen tener la misma «fase».
  • El ángulo variable en el tiempo {displaystyle 2\pi ft+\theta ,\\} o su valor modulo {displaystyle 2\pi }, también se denomina comúnmente «fase». Entonces no es una condición inicial, sino una condición que cambia continuamente.

El término fase instantánea se utiliza para distinguir el ángulo variable en el tiempo de la condición inicial. También tiene una definición formal que es aplicable a funciones más generales y define inequívocamente la fase inicial de una función en t=0. Es decir, el seno y el coseno tienen inherentemente fases iniciales diferentes. Cuando no se indica explícitamente lo contrario, el coseno debe inferirse generalmente. (ver también fasor)

Desplazamiento de fase

File:Phase shift.png

Ilustración del desplazamiento de fase. El eje horizontal representa un ángulo (fase) que aumenta con el tiempo.

{displaystyle \theta } a veces se denomina desplazamiento de fase, porque representa un «desplazamiento» desde la fase cero. Pero un cambio en {displaystyle \theta } también se denomina desplazamiento de fase.

Para sinusoides infinitamente largos, un cambio en {displaystyle \theta } es lo mismo que un desplazamiento en el tiempo, como un retraso de tiempo. Si {displaystyle x(t)\} se retrasa (se desplaza en el tiempo) en {displaystyle {\begin{matrix}{frac {1}{4}{end{matrix}},} de su ciclo, se convierte:

{displaystyle x(t-{begin{matrix}{frac {1}{4}{end{matrix}})}, {displaystyle =A\cdot \sin(2\pi f(t-{begin{matrix}{frac {1}{4}{end{matrix}}T)+\theta )},}
{sin(2\cdot ft-{begin{matrix}{frac {\pi}{2}{end{matrix}}+theta ),

cuya «fase» es ahora {{muestra \theta -{in{matriz}{frac {\pi }{2}{final{matriz}}. Se ha desplazado en {displaystyle {\begin{matrix}{\frac {\pi}{2}{end{matrix}}.

Diferencia de fase

File:Sine waves same phase.svg

Ondas en fase

File:Sine waves different phase.svg

Ondas fuera de fase

File:Phase-shift illustration.png

Izquierda: la parte real de una onda plana moviéndose de arriba a abajo. Derecha: la misma onda después de que una sección central sufriera un desplazamiento de fase, por ejemplo, al atravesar un vidrio de diferente grosor que las otras partes. (La ilustración de la derecha ignora el efecto de la difracción, cuyo efecto aumenta a grandes distancias).

Dos osciladores que tienen la misma frecuencia y diferentes fases tienen una diferencia de fase, y se dice que los osciladores están desfasados entre sí. La cantidad en que dichos osciladores están desfasados entre sí puede expresarse en grados de 0° a 360°, o en radianes de 0 a 2π. Si la diferencia de fase es de 180 grados (π radianes), se dice que los dos osciladores están en antifase. Si dos ondas que interactúan se encuentran en un punto en el que están en antifase, se producirá una interferencia destructiva. Es habitual que las ondas electromagnéticas (luz, RF), acústicas (sonido) o de otro tipo se superpongan en su medio de transmisión. Cuando esto ocurre, la diferencia de fase determina si se refuerzan o debilitan mutuamente. La cancelación completa es posible para las ondas con amplitudes iguales.

El tiempo se utiliza a veces (en lugar del ángulo) para expresar la posición dentro del ciclo de una oscilación.

  • Una diferencia de fase es análoga a la de dos atletas que corren alrededor de una pista de carreras a la misma velocidad y en la misma dirección pero que comienzan en diferentes posiciones en la pista. Pasan por un punto en diferentes instantes de tiempo. Pero la diferencia de tiempo (diferencia de fase) entre ellos es una constante – la misma para cada pasada ya que están a la misma velocidad y en la misma dirección. Si estuvieran a diferentes velocidades (diferentes frecuencias), la diferencia de fase sólo reflejaría diferentes posiciones de partida.
  • Medimos la rotación de la tierra en horas, en lugar de radianes. Y por tanto los husos horarios son un ejemplo de diferencias de fase.

Componentes en fase y cuadratura (I&Q)

El término en fase también se encuentra en el contexto de las señales de comunicación:

{{displaystyle A(t)\cdot \sin=I(t)\cdot \sin(2\pi ft)+Q(t)\cdot \cbrace {\cos(2\pi ft)} y:{displaystyle A(t)\cdot \ccos=I(t)\cdot \ccos(2\pi ft)\cunderbrace {-Q(t)\cdot \sin(2\pi ft)} Q(t)\cdot \ccos \left(2\pi ft+{{begin{matrix}{frac {\pi}{2}}end{matrix}{right)}

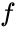
donde {displaystyle f,} representa una frecuencia portadora, y

{displaystyle I(t)}{{stackrel {\mathrm {def}} A(t)\}{cdot \cos,\}{displaystyle Q(t)\} {\stackrel {\mathrm {def} A(t)\cdot \sin.\},}

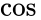
{displaystyle A(t)\c,} y {displaystyle \phi (t)\c,} representan la posible modulación de una onda portadora pura, por ejemplo: {displaystyle \sin(2\pi ft).\} La modulación altera la componente original {displaystyle \sin \} de la portadora, y crea una (nueva) componente {displaystyle \cos \}, como se muestra arriba. El componente que está en fase con la portadora original se denomina componente en fase. La otra componente, que siempre está a 90° ({displaystyle {\begin{matrix}{\frac {\pi }{2}}\matrix}} radianes) «fuera de fase», se denomina componente de cuadratura.

Coherencia de fase

La coherencia es la cualidad de una onda de mostrar una relación de fase bien definida en diferentes regiones de su dominio de definición.

En física, la mecánica cuántica atribuye ondas a los objetos físicos. La función de onda es compleja y como su módulo cuadrado está asociado a la probabilidad de observar el objeto, el carácter complejo de la función de onda está asociado a la fase. Dado que el álgebra compleja es responsable del sorprendente efecto de interferencia de la mecánica cuántica, la fase de las partículas está por tanto relacionada en última instancia con su comportamiento cuántico.

Deja una respuesta

Tu dirección de correo electrónico no será publicada.