Bien que les méthodes de la section précédente soient utiles pour décrire et afficher des données d’échantillon, la véritable puissance des statistiques se révèle lorsque nous utilisons des échantillons pour nous donner des informations sur des populations. Dans ce contexte, une population est la collection entière d’objets d’intérêt, par exemple, les prix de vente de toutes les maisons unifamiliales sur le marché du logement représenté par notre ensemble de données. Nous aimerions en savoir plus sur cette population pour nous aider à prendre une décision sur la maison à acheter, mais les seules données dont nous disposons sont un échantillon aléatoire de 30 prix de vente.
Néanmoins, nous pouvons employer la « pensée statistique » pour tirer des inférences sur la population d’intérêt en analysant les données de l’échantillon. En particulier, nous utilisons la notion de modèle – une abstraction mathématique du monde réel – que nous adaptons aux données de l’échantillon. Si ce modèle s’adapte raisonnablement aux données, c’est-à-dire s’il peut approcher la manière dont les données varient, nous supposons alors qu’il peut également approcher le comportement de la population. Le modèle sert alors de base à la prise de décisions concernant la population, par exemple en identifiant des modèles, en expliquant les variations et en prédisant les valeurs futures. Bien sûr, ce processus ne peut fonctionner que si les données de l’échantillon peuvent être considérées comme représentatives de la population.
Parfois, même lorsque nous savons qu’un échantillon n’a pas été choisi au hasard, nous pouvons quand même le modéliser. Alors, nous pouvons ne pas être en mesure de déduire formellement une population à partir de l’échantillon, mais nous pouvons toujours modéliser la structure sous-jacente de l’échantillon. Un exemple serait un échantillon de commodité – un échantillon sélectionné plus pour des raisons de commodité que pour ses propriétés statistiques. Lorsque l’on modélise ce type d’échantillon, les résultats doivent être accompagnés d’une mise en garde contre le risque de limiter les conclusions à des objets similaires à ceux de l’échantillon. Un autre type d’exemple est celui où l’échantillon comprend l’ensemble de la population. Par exemple, nous pourrions modéliser les données des 50 États des États-Unis d’Amérique afin de mieux comprendre tout modèle ou association systématique entre les États.
Puisque le monde réel peut être extrêmement compliqué (dans la façon dont les valeurs des données varient ou interagissent ensemble), les modèles sont utiles car ils simplifient les problèmes afin que nous puissions mieux les comprendre (et ensuite prendre des décisions plus efficaces). D’une part, nous avons donc besoin de modèles suffisamment simples pour pouvoir les utiliser facilement pour prendre des décisions, mais d’autre part, nous avons besoin de modèles suffisamment flexibles pour fournir de bonnes approximations de situations complexes. Heureusement, de nombreux modèles statistiques ont été développés au fil des ans et offrent un équilibre efficace entre ces deux critères. Un de ces modèles, qui fournit un bon point de départ pour les modèles plus compliqués que nous considérons plus tard, est la distribution normale.
D’un point de vue statistique, une distribution de probabilité est un modèle théorique qui décrit comment une variable aléatoire varie. Pour nos besoins, une variable aléatoire représente les valeurs de données d’intérêt dans la population, par exemple, les prix de vente de toutes les maisons unifamiliales dans notre marché du logement. La distribution des valeurs de données dans la population peut être représentée par un histogramme, comme décrit dans la section 1.1. La différence est que l’histogramme affiche l’ensemble de la population plutôt que l’échantillon. Puisque la population est tellement plus grande que l’échantillon, les bacs de l’histogramme (les plages consécutives des données qui comprennent les intervalles horizontaux des barres) peuvent être beaucoup plus petits, par exemple, ce qui suit montre un histogramme pour une population simulée de 1 000 prix de vente.
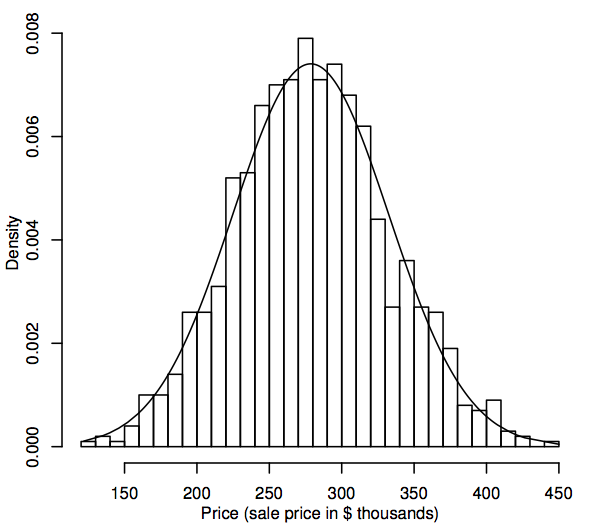
A mesure que la taille de la population augmente, on peut imaginer que les barres de l’histogramme deviennent plus fines et plus nombreuses, jusqu’à ce que l’histogramme ressemble à une courbe lisse plutôt qu’à une série de paliers. Cette courbe lisse s’appelle une courbe de densité et peut être considérée comme la version théorique de l’histogramme de population. Les courbes de densité fournissent également un moyen de visualiser les distributions de probabilité telles que la distribution normale. Une courbe de densité normale est superposée à l’histogramme ci-dessus. L’histogramme de la population simulée suit la courbe d’assez près, ce qui suggère que cette distribution de population simulée est assez proche de la normale.
Pour voir comment une distribution théorique peut s’avérer utile pour faire des inférences statistiques sur des populations telles que celle de notre exemple sur les prix des maisons, nous devons examiner de plus près la distribution normale. Pour commencer, nous considérons une version particulière de la distribution normale, la normale standard, représentée par la courbe de densité suivante.
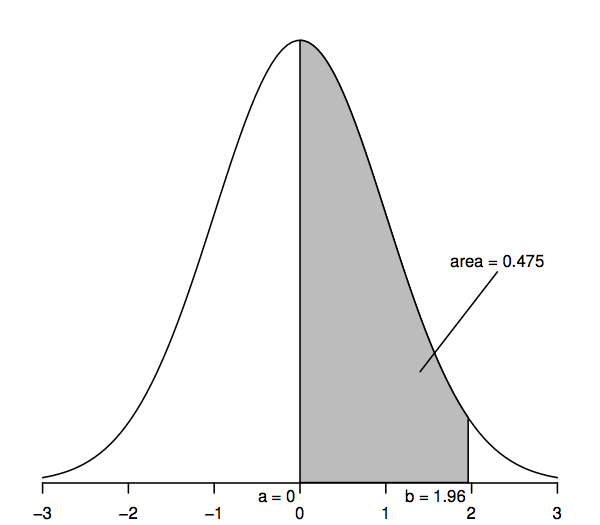
Les variables aléatoires qui suivent une distribution normale standard ont une moyenne de 0 (la courbe est donc symétrique autour de 0, qui est sous le point le plus haut de la courbe) et un écart-type de 1 (la courbe a donc un point d’inflexion – où la courbe s’incurve d’abord dans un sens puis dans l’autre – à +1 et -1). La courbe de densité normale est parfois appelée « courbe en cloche » car sa forme ressemble à celle d’une cloche.
La caractéristique clé de la courbe de densité normale qui nous permet de faire des inférences statistiques est que les zones sous la courbe représentent des probabilités. L’aire entière sous la courbe est égale à un, tandis que l’aire sous la courbe entre un point sur l’axe horizontal (a, disons) et un autre point (b, disons) représente la probabilité qu’une variable aléatoire qui suit une distribution normale standard se situe entre a et b. Ainsi, par exemple, la figure ci-dessus montre que la probabilité est de 0.475 qu’une variable aléatoire normale standard se situe entre a=0 et b=1,96, puisque l’aire sous la courbe entre a=0 et b=1,96 est de 0,475.
Nous pouvons obtenir les valeurs de ces aires ou probabilités à partir de diverses sources : tableaux de chiffres, calculatrices, tableurs ou logiciels statistiques, sites Web, etc. Nous n’imprimons ci-dessous que quelques valeurs sélectionnées, car la plupart des calculs ultérieurs utilisent une généralisation de la distribution normale appelée « distribution t ». De plus, plutôt que des zones telles que celle ombrée dans la figure ci-dessus, il sera plus utile de considérer les « zones de queue » (par ex, à droite du point b), et donc, par souci de cohérence avec les tableaux de nombres ultérieurs, le tableau suivant permet de calculer de telles aires de queue :
En particulier, l’aire de queue supérieure à droite de 1,96 est de 0,025 ; cela revient à dire que l’aire entre 0 et 1,96 est de 0,475 (puisque toute l’aire sous la courbe est de 1 et que l’aire à droite de 0 est de 0,5). De même, l’aire à deux queues, qui est la somme des aires à droite de 1,96 et à gauche de -1,96, est deux fois 0,025, soit 0,05.
Comment tout cela nous aide-t-il à faire des inférences statistiques sur des populations telles que celle de notre exemple sur les prix des maisons ? L’idée essentielle est que nous ajustons un modèle de distribution normale à nos données d’échantillon, puis utilisons ce modèle pour faire des inférences sur la population correspondante. Par exemple, nous pouvons utiliser les calculs de probabilité d’une distribution normale (comme le montre la figure ci-dessus) pour faire des déclarations de probabilité sur une population modélisée à l’aide de cette distribution normale – nous montrerons exactement comment faire dans la section 1.3. Mais avant cela, nous devons nous arrêter sur un aspect de cette séquence inférentielle qui peut faire ou défaire le processus. Le modèle fournit-il une approximation suffisamment proche du modèle des valeurs de l’échantillon pour que nous puissions être sûrs que le modèle représente correctement les valeurs de la population ? Plus l’approximation est bonne, plus nos déclarations inférentielles seront fiables.
Nous avons vu précédemment comment une courbe de densité peut être considérée comme un histogramme avec une très grande taille d’échantillon. Ainsi, une façon d’évaluer si notre population suit un modèle de distribution normale est de construire un histogramme à partir des données de notre échantillon et de déterminer visuellement s’il » semble normal « , c’est-à-dire approximativement symétrique et en forme de cloche. Il s’agit d’une décision quelque peu subjective, mais avec l’expérience, vous devriez constater qu’il devient plus facile de distinguer les histogrammes clairement non normaux de ceux qui sont raisonnablement normaux. Par exemple, alors que l’histogramme ci-dessus ressemble clairement à une courbe de densité normale, la normalité de l’histogramme de 30 échantillons de prix de vente de la section 1.1 est moins certaine. Une conclusion raisonnable dans ce cas serait que si cet histogramme d’échantillon n’est pas parfaitement symétrique et en forme de cloche, il en est suffisamment proche pour que l’histogramme de population (hypothétique) correspondant puisse bien être normal.
Une autre façon d’évaluer la normalité est de construire un QQ-plot (quantile-quantile plot), également connu sous le nom de diagramme de probabilité normale, comme indiqué ici pour les données sur les prix de l’immobilier :
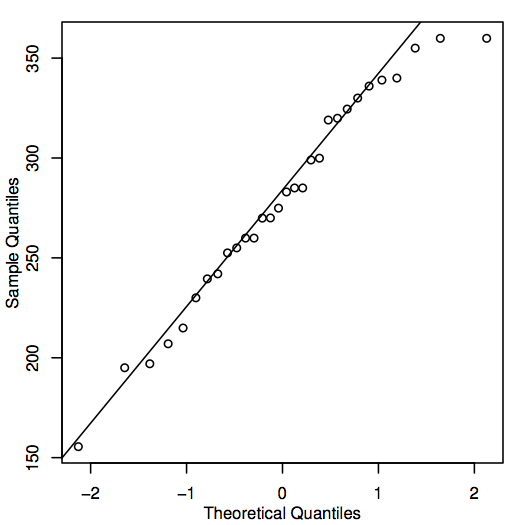
Si les points du QQ-plot sont proches de la ligne diagonale, alors les valeurs de population correspondantes pourraient bien être normales. Si les points se situent généralement loin de la ligne, alors la normalité est remise en question. Là encore, il s’agit d’une décision quelque peu subjective qui devient plus facile à prendre avec l’expérience. Dans ce cas, étant donné la taille assez réduite de l’échantillon, les points sont probablement assez proches de la ligne pour qu’il soit raisonnable de conclure que les valeurs de la population pourraient être normales.
Il existe également une variété de méthodes quantitatives pour évaluer la normalité – voir la section 6.3.
.