Définition
Un polynôme dans la variable x est une fonction qui peut être écrite sous la forme,
où an, an-1 , …, a2, a1, a0 sont des constantes. On appelle le terme contenant la plus grande puissance de x (c’est-à-dire anxn) le terme de tête, et on appelle an le coefficient de tête. Le degré du polynôme est la puissance de x dans le terme principal. Nous avons déjà vu les polynômes de degré 0, 1 et 2 qui étaient respectivement les fonctions constantes, linéaires et quadratiques. Les polynômes de degré 3, 4 et 5 ont également des noms spéciaux : fonctions cubique, quartique et quintique. Les polynômes de degré n > 5 sont simplement appelés polynômes de nième degré. Les noms des différentes fonctions polynomiales sont résumés dans le tableau ci-dessous.
| Degree du polynôme | Nom de la fonction |
| 0 | Fonction constante. |
| 1 | Fonction linéaire |
| 2 | Fonction quadratique |
| 3 | Fonction cubique |
| 4 | Fonction quartique |
| 5 | Fonction quintique |
| n (où n > 5) | Polynôme de nième degré |
Certains exemples de polynômes comprennent :
Le comportement limite des polynômes
Le comportement limite d’une fonction décrit ce qui arrive à la fonction lorsque x → ±∞. Le degré d’un polynôme et le signe de son coefficient principal dictent son comportement limite. En particulier,
Ces résultats sont résumés dans le tableau ci-dessous.
Vous pouvez utiliser ces informations pour déterminer si un polynôme a un degré impair ou pair et si le coefficient directeur est positif ou négatif, simplement en inspectant son graphique.
Les graphes suivants de polynômes exemplifient chacun des comportements décrits dans le tableau ci-dessus.
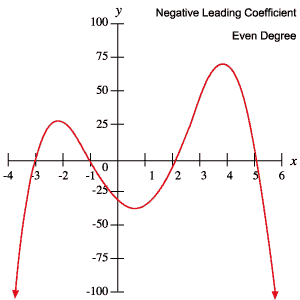
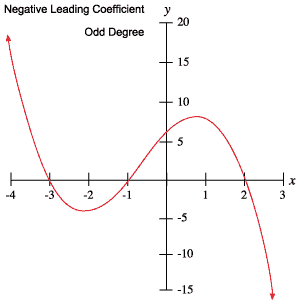
Roots et points tournants
Le degré d’un polynôme vous en dit encore plus sur lui que le comportement limite. Plus précisément, un polynôme de nième degré peut avoir au plus n racines réelles (x-intercepts ou zéros) en comptant les multiplicités. Par exemple, supposons que nous examinions un polynôme du 6e degré qui a 4 racines distinctes. Si deux des quatre racines ont une multiplicité de 2 et les deux autres une multiplicité de 1, nous savons qu’il n’y a pas d’autres racines car nous avons pris en compte les 6 racines. Cela est dû au fait que les racines ayant une multiplicité de deux (également connues sous le nom de racines doubles) sont comptées comme deux racines.
Sachez qu’un polynôme de nième degré n’a pas nécessairement n racines réelles – il pourrait en avoir moins car il a des racines imaginaires. Remarquez qu’un polynôme de degré impair doit avoir au moins une racine réelle puisque la fonction s’approche de – ∞ à une extrémité et de + ∞ à l’autre ; une fonction continue qui passe du négatif au positif doit couper l’axe des x quelque part entre les deux. En outre, un polynôme de nième degré peut avoir au plus n – 1 points de retournement. Un point d’inflexion est un point auquel la fonction passe de l’augmentation à la diminution ou de la diminution à l’augmentation, comme le montre la figure ci-dessous. Encore une fois, un polynôme de nième degré ne doit pas nécessairement avoir n – 1 points de retournement, il pourrait en avoir moins.
Note de prudence
Il est important de réaliser la différence entre les fonctions paires et impaires et les polynômes de degré pair et impair. Toute fonction, f(x), est soit paire si,
f(-x) = x,
pour tout x dans le domaine de f(x), soit impaire si,
f(-x) = -x,
pour tout x dans le domaine de f(x), ou ni paire ni impaire si aucune des affirmations ci-dessus n’est vraie.
Un polynôme de kième degré, p(x), est dit de degré pair si k est un nombre pair et de degré impair si k est un nombre impair. Rappelez-vous que même si p(x) a un degré pair, ce n’est pas nécessairement une fonction paire. De même, si p(x) a un degré impair, ce n’est pas nécessairement une fonction impaire.
Nous utilisons également les termes pair et impair pour décrire les racines des polynômes. Plus précisément, un polynôme p(x) a une racine x = a de multiplicité k (c’est-à-dire que x = a est une racine répétée k fois) si (x – a)k est un facteur de p(x). On dit que x = a a une multiplicité paire si k est un nombre pair et une multiplicité impaire si k est un nombre impair.
Domaine et étendue
Tous les polynômes ont le même domaine qui est constitué de tous les nombres réels. L’étendue des polynômes de degré impair est également constituée de tous les nombres réels. Le domaine des polynômes de degré pair est un peu plus compliqué et nous ne pouvons pas énoncer explicitement le domaine de tous les polynômes de degré pair. Si le coefficient principal est positif, la fonction s’étendra jusqu’à + ∞ ; tandis que si le coefficient principal est négatif, elle s’étendra jusqu’à – ∞. Cela signifie que les polynômes de degré pair dont le coefficient principal est positif ont une étendue où ymax désigne le maximum global atteint par la fonction. En général, il n’est pas possible de déterminer analytiquement les maxima ou minima des polynômes.
*****
Dans la prochaine section, vous apprendrez la division polynomiale, une technique utilisée pour trouver les racines des fonctions polynomiales.
Division polynomiale
.