Introduction

Imaginez ceci : on vous a chargé de prévoir le prix du prochain iPhone et on vous a fourni des données historiques. Celles-ci comprennent des caractéristiques comme les ventes trimestrielles, les dépenses mensuelles et tout un tas de choses qui accompagnent le bilan d’Apple. En tant que spécialiste des données, quel type de problème classeriez-vous dans cette catégorie ? La modélisation des séries temporelles, bien sûr.

De la prévision des ventes d’un produit à l’estimation de la consommation d’électricité des ménages, la prévision des séries temporelles est l’une des compétences de base que tout data scientist est censé connaître, voire maîtriser. Il existe une pléthore de techniques différentes que vous pouvez utiliser, et nous allons couvrir l’une des plus efficaces, appelée Auto ARIMA, dans cet article.

Nous allons d’abord comprendre le concept d’ARIMA qui nous mènera à notre sujet principal – Auto ARIMA. Pour solidifier nos concepts, nous allons prendre un jeu de données et l’implémenter à la fois en Python et en R.

Table des matières

1. Qu’est-ce qu’une série temporelle ?
2. Méthodes de prévision des séries temporelles
3. Introduction à l’ARIMA
4. Étapes de l’implémentation de l’ARIMA
5. Pourquoi avons-nous besoin d’AutoARIMA ?
6. Mise en œuvre de l’ARIMA automatique (sur le jeu de données des passagers aériens)
7. Comment l’ARIMA automatique sélectionne-t-il les paramètres ?

Si vous êtes familier avec les séries temporelles et ses techniques (comme la moyenne mobile, le lissage exponentiel et l’ARIMA), vous pouvez passer directement à la section 4. Pour les débutants, commencez par la section ci-dessous qui est une brève introduction aux séries temporelles et aux différentes techniques de prévision.

Qu’est-ce qu’une série temporelle ?

Avant de connaître les techniques pour travailler sur les données de séries temporelles, nous devons d’abord comprendre ce qu’est réellement une série temporelle et en quoi elle est différente de tout autre type de données. Voici la définition formelle de la série temporelle – C’est une série de points de données mesurés à des intervalles de temps cohérents. Cela signifie simplement que des valeurs particulières sont enregistrées à un intervalle constant qui peut être horaire, quotidien, hebdomadaire, tous les 10 jours, etc. Ce qui différencie les séries chronologiques, c’est que chaque point de données de la série dépend des points de données précédents. Comprenons plus clairement la différence en prenant quelques exemples.

Exemple 1:

Supposons que vous avez un ensemble de données de personnes qui ont pris un prêt auprès d’une entreprise particulière (comme indiqué dans le tableau ci-dessous). Pensez-vous que chaque rangée sera liée aux rangées précédentes ? Certainement pas ! Le prêt contracté par une personne sera basé sur ses conditions financières et ses besoins (il peut y avoir d’autres facteurs comme la taille de la famille, etc., mais pour simplifier, nous ne considérons que le revenu et le type de prêt). En outre, les données n’ont pas été collectées à un intervalle de temps spécifique. Cela dépend du moment où l’entreprise a reçu une demande de prêt.

Exemple 2:

Prenons un autre exemple. Supposons que vous ayez un ensemble de données qui contient le niveau de CO2 dans l’air par jour (capture d’écran ci-dessous). Serez-vous capable de prédire la quantité approximative de CO2 pour le jour suivant en regardant les valeurs des derniers jours ? Oui, bien sûr. Si vous observez, les données ont été enregistrées sur une base quotidienne, c’est-à-dire que l’intervalle de temps est constant (24 heures).

Vous devez avoir une intuition à ce sujet maintenant – le premier cas est un problème de régression simple et le second est un problème de série chronologique. Bien que le puzzle de la série temporelle ici puisse également être résolu en utilisant la régression linéaire, mais ce n’est pas vraiment la meilleure approche car elle néglige la relation des valeurs avec toutes les valeurs passées relatives. Voyons maintenant quelques-unes des techniques courantes utilisées pour résoudre les problèmes de séries temporelles.

Méthodes de prévision des séries temporelles

Il existe un certain nombre de méthodes de prévision des séries temporelles et nous allons les aborder brièvement dans cette section. L’explication détaillée et les codes python pour toutes les techniques mentionnées ci-dessous peuvent être trouvés dans cet article : 7 techniques de prévision des séries temporelles (avec codes python).

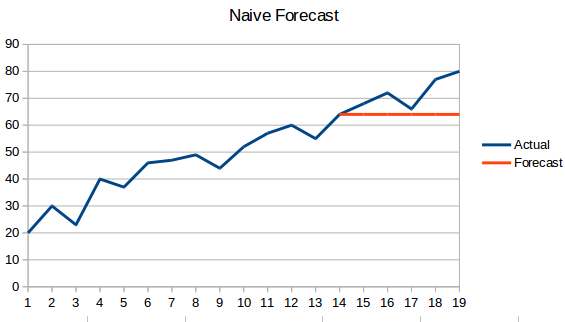
1. Approche naïve : Dans cette technique de prévision, la valeur du nouveau point de données est prédite comme étant égale au point de données précédent. Le résultat serait une ligne plate, puisque toutes les nouvelles valeurs prennent les valeurs précédentes.
2. Moyenne simple : La prochaine valeur est prise comme la moyenne de toutes les valeurs précédentes. Les prédictions sont ici meilleures que l' » approche naïve  » car elles ne donnent pas lieu à une ligne plate, mais ici, toutes les valeurs passées sont prises en compte, ce qui n’est pas toujours utile. Par exemple, si on vous demande de prédire la température d’aujourd’hui, vous considérerez la température des 7 derniers jours plutôt que celle d’il y a un mois.
3. Moyenne mobile : C’est une amélioration par rapport à la technique précédente. Au lieu de prendre la moyenne de tous les points précédents, on prend la moyenne de ‘n’ points précédents pour être la valeur prédite.
4. Moyenne mobile pondérée : Une moyenne mobile pondérée est une moyenne mobile où les ‘n’ valeurs passées ont des poids différents.
5. Lissage exponentiel simple : Dans cette technique, des poids plus importants sont attribués aux observations plus récentes qu’aux observations du passé lointain.
6. Modèle linéaire à tendance de Holt : Cette méthode prend en compte la tendance de l’ensemble des données. Par tendance, on entend le caractère croissant ou décroissant de la série. Supposons que le nombre de réservations dans un hôtel augmente chaque année, on peut alors dire que le nombre de réservations présente une tendance croissante. La fonction de prévision dans cette méthode est une fonction du niveau et de la tendance.
7. Méthode Holt Winters : Cet algorithme prend en compte à la fois la tendance et la saisonnalité de la série. Par exemple – le nombre de réservations dans un hôtel est élevé le week-end & faible en semaine, et augmente chaque année ; il existe une saisonnalité hebdomadaire et une tendance croissante.
8. ARIMA : L’ARIMA est une technique très populaire pour la modélisation des séries temporelles. Elle décrit la corrélation entre les points de données et prend en compte la différence des valeurs. Une amélioration de l’ARIMA est le SARIMA (ou ARIMA saisonnier). Nous allons examiner l’ARIMA un peu plus en détail dans la section suivante.

Introduction à l’ARIMA

Dans cette section, nous allons faire une introduction rapide à l’ARIMA qui sera utile pour comprendre Auto Arima. Une explication détaillée d’Arima, des paramètres (p,q,d), des parcelles (ACF PACF) et de la mise en œuvre est incluse dans cet article : Tutoriel complet sur les séries temporelles.

ARIMA est une méthode statistique très populaire pour la prévision des séries temporelles. ARIMA est l’abréviation de Auto-Regressive Integrated Moving Averages. Les modèles ARIMA fonctionnent sur les hypothèses suivantes –

• La série de données est stationnaire, ce qui signifie que la moyenne et la variance ne doivent pas varier dans le temps. Une série peut être rendue stationnaire en utilisant une transformation logarithmique ou en différenciant la série.
• Les données fournies en entrée doivent être une série univariée, car l’arima utilise les valeurs passées pour prédire les valeurs futures.

L’arima a trois composantes – AR (terme autorégressif), I (terme de différenciation) et MA (terme de moyenne mobile). Comprenons chacune de ces composantes –

• Le terme AR fait référence aux valeurs passées utilisées pour prévoir la valeur suivante. Le terme AR est défini par le paramètre ‘p’ dans arima. La valeur de ‘p’ est déterminée à l’aide du graphe PACF.
• Le terme MA est utilisé pour définir le nombre d’erreurs de prévision passées utilisées pour prévoir les valeurs futures. Le paramètre ‘q’ dans arima représente le terme MA. Le tracé ACF est utilisé pour identifier la valeur correcte de ‘q’.
• L’ordre de différenciation spécifie le nombre de fois que l’opération de différenciation est effectuée sur la série pour la rendre stationnaire. Des tests comme ADF et KPSS peuvent être utilisés pour déterminer si la série est stationnaire et aider à identifier la valeur d.

Étapes pour la mise en œuvre d’ARIMA

Les étapes générales pour mettre en œuvre un modèle ARIMA sont –

1. Charger les données : La première étape pour la construction du modèle est bien sûr de charger l’ensemble de données
2. Prétraitement : En fonction du jeu de données, les étapes du prétraitement seront définies. Il s’agira notamment de créer des timestamps, de convertir le dtype de la colonne date/heure, de rendre les séries univariées, etc.
3. Rendre les séries stationnaires : Afin de satisfaire l’hypothèse, il est nécessaire de rendre les séries stationnaires. Il s’agirait de vérifier la stationnarité de la série et d’effectuer les transformations requises
4. Déterminer la valeur de d : Pour rendre la série stationnaire, le nombre de fois où l’opération de différence a été effectuée sera pris comme la valeur d
5. Créer des graphiques ACF et PACF : C’est l’étape la plus importante dans la mise en œuvre de l’ARIMA. Les tracés ACF PACF sont utilisés pour déterminer les paramètres d’entrée de notre modèle ARIMA
6. Déterminer les valeurs de p et q : Lire les valeurs de p et q à partir des tracés de l’étape précédente
7. Ajuster le modèle ARIMA : En utilisant les données traitées et les valeurs des paramètres que nous avons calculées à partir des étapes précédentes, ajustez le modèle ARIMA
8. Prédire les valeurs sur l’ensemble de validation : Prédire les valeurs futures
9. Calculer RMSE : Pour vérifier la performance du modèle, vérifiez la valeur RMSE en utilisant les prédictions et les valeurs réelles sur l’ensemble de validation

Pourquoi avons-nous besoin d’Auto ARIMA ?

Bien que l’ARIMA soit un modèle très puissant pour prévoir les données de séries temporelles, les processus de préparation des données et de réglage des paramètres finissent par être vraiment chronophages. Avant de mettre en œuvre ARIMA, vous devez rendre les séries stationnaires et déterminer les valeurs de p et q à l’aide des graphiques que nous avons abordés plus haut. Auto ARIMA nous simplifie vraiment la tâche en éliminant les étapes 3 à 6 que nous avons vues dans la section précédente. Voici les étapes que vous devez suivre pour mettre en œuvre l’ARIMA automatique :

1. Chargez les données : Cette étape sera la même. Chargez les données dans votre notebook
2. Prétraitement des données : L’entrée doit être univariée, donc laissez tomber les autres colonnes
3. Fit Auto ARIMA : Ajustez le modèle sur les séries univariées
4. Prédire les valeurs sur l’ensemble de validation : Faire des prédictions sur l’ensemble de validation
5. Calculer RMSE : Vérifier la performance du modèle en utilisant les valeurs prédites par rapport aux valeurs réelles

Nous avons complètement contourné la sélection de la caractéristique p et q comme vous pouvez le voir. Quel soulagement ! Dans la section suivante, nous allons implémenter l’auto ARIMA en utilisant un jeu de données jouet.

Implémentation en Python et R

Nous allons utiliser le jeu de données International-Air-Passenger. Ce jeu de données contient le total mensuel du nombre de passagers (en milliers). Il comporte deux colonnes – le mois et le nombre de passagers. Vous pouvez télécharger le jeu de données à partir de ce lien.

#load the datadata = pd.read_csv('international-airline-passengers.csv')#divide into train and validation settrain = datavalid = data#preprocessing (since arima takes univariate series as input)train.drop('Month',axis=1,inplace=True)valid.drop('Month',axis=1,inplace=True)#plotting the datatrain.plot()valid.plot()

#building the modelfrom pyramid.arima import auto_arimamodel = auto_arima(train, trace=True, error_action='ignore', suppress_warnings=True)model.fit(train)forecast = model.predict(n_periods=len(valid))forecast = pd.DataFrame(forecast,index = valid.index,columns=)#plot the predictions for validation setplt.plot(train, label='Train')plt.plot(valid, label='Valid')plt.plot(forecast, label='Prediction')plt.show()

#calculate rmsefrom math import sqrtfrom sklearn.metrics import mean_squared_errorrms = sqrt(mean_squared_error(valid,forecast))print(rms)

output -76.51355764316357

Vous trouverez ci-dessous le code R pour le même problème:

# loading packageslibrary(forecast)library(Metrics)# reading datadata = read.csv("international-airline-passengers.csv")# splitting data into train and valid setstrain = datavalid = data# removing "Month" columntrain$Month = NULL# training modelmodel = auto.arima(train)# model summarysummary(model)# forecastingforecast = predict(model,44)# evaluationrmse(valid$International.airline.passengers, forecast$pred)

Comment Auto Arima sélectionne-t-il les meilleurs paramètres

Dans le code ci-dessus, nous avons simplement utilisé la commande .fit() pour ajuster le modèle sans avoir à sélectionner la combinaison de p, q, d. Mais comment le modèle a-t-il déterminé la meilleure combinaison de ces paramètres ? Auto ARIMA prend en compte les valeurs AIC et BIC générées (comme vous pouvez le voir dans le code) pour déterminer la meilleure combinaison de paramètres. Les valeurs AIC (Akaike Information Criterion) et BIC (Bayesian Information Criterion) sont des estimateurs permettant de comparer les modèles. Plus ces valeurs sont faibles, meilleur est le modèle.

Voyez ces liens si vous êtes intéressé par les mathématiques derrière l’AIC et le BIC.

Notes de fin et lectures complémentaires

J’ai trouvé que l’auto ARIMA est la technique la plus simple pour effectuer des prévisions de séries temporelles. Connaître un raccourci, c’est bien, mais être familier avec les mathématiques derrière est également important. Dans cet article, j’ai survolé les détails du fonctionnement de l’ARIMA, mais assurez-vous de consulter les liens fournis dans l’article. Pour votre référence facile, voici à nouveau les liens :

• Un guide complet pour les débutants sur la prévision des séries temporelles en Python
• Tutoriel complet sur les séries temporelles en R
• 7 techniques pour la prévision des séries temporelles (avec des codes python)

Je vous suggère de mettre en pratique ce que nous avons appris ici sur ce problème pratique : Problème pratique sur les séries temporelles. Vous pouvez également suivre notre cours de formation créé sur le même problème pratique, Prévisions de séries temporelles, pour vous donner une longueur d’avance.