Le réseau de croyance bayésien ou réseau bayésien ou réseau de croyance est un modèle graphique probabiliste (MGP) qui représente les dépendances conditionnelles entre variables aléatoires à travers un graphe acyclique dirigé (DAG).
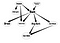
Aujourd’hui, je vais essayer d’expliquer les principaux aspects des réseaux de croyance, en particulier pour les applications qui peuvent être liées à l’analyse des réseaux sociaux(SNA). En outre, je vous montrerai un exemple de mise en œuvre de ce type de réseau.
À quoi servent les réseaux bayésiens ?
Les réseaux bayésiens sont appliqués dans de nombreux domaines. Par exemple, le diagnostic des maladies, la recherche optimisée sur le web, le filtrage du spam, les réseaux de régulation des gènes, etc. Et cette liste peut être étendue. L’objectif principal de ces réseaux est d’essayer de comprendre la structure des relations de causalité. Pour clarifier ce point, considérons un problème de diagnostic de maladie. Avec des symptômes donnés et la maladie qui en résulte, nous construisons notre réseau de croyance et lorsqu’un nouveau patient arrive, nous pouvons déduire quelle(s) maladie(s) peut (peuvent) avoir le nouveau patient en fournissant des probabilités pour chaque maladie. De même, ces relations de causalité peuvent être construites pour d’autres problèmes et les techniques d’inférence peuvent être appliquées à des résultats intéressants.
Revue rapide sur les probabilités
Avant de continuer, pour nous rafraîchir la mémoire, laissez-moi vous donner la définition de la propriété conditionnelle. La probabilité conditionnelle est la probabilité d’une variable aléatoire lorsqu’une autre variable aléatoire est donnée. On la démontre par
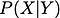
Si ces deux variables aléatoires sont dépendantes,
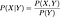
Si elles sont indépendantes, alors
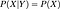
Définition mathématique des réseaux de croyance
Les probabilités sont calculées dans les réseaux de croyance par la formule suivante
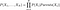
Comme vous le comprenez par la formule, pour pouvoir calculer la distribution conjointe, nous devons avoir les probabilités conditionnelles indiquées par le réseau. Mais en outre, si nous avons la distribution conjointe, alors nous pouvons commencer à poser des questions intéressantes. Par exemple, dans le premier exemple, nous demandons la probabilité de « PLUIE » si « SAISON » est « HIVER » et « ABOIEMENT DE CHIEN » est « VRAI ».
Exemple Python de réseau de croyance
Alors, je pense que cela suffit pour la théorie et voyons un exemple réel avec mon langage de programmation préféré actuel Python ❤️ Avant de continuer, vous pouvez trouver le carnet Jupyter que j’ai écrit ici.
# create the nodes
season = BbnNode(Variable(0, 'season', ), )
atmos_pres = BbnNode(Variable(1, 'atmos_press', ), )
allergies = BbnNode(Variable(2, 'allergies', ), )
rain = BbnNode(Variable(3, 'rain', ), )
grass = BbnNode(Variable(4, 'grass', ), )
umbrellas = BbnNode(Variable(5, 'umbrellas', ), )
dog_bark = BbnNode(Variable(6, 'dog_bark', ), )
cat_mood = BbnNode(Variable(7, 'cat_mood', ), )
cat_hide = BbnNode(Variable(8, 'cat_hide', ), )bbn = Bbn() \
.add_node(season) \
.add_node(atmos_pres) \
.add_node(allergies) \
.add_node(rain) \
.add_node(grass) \
.add_node(umbrellas) \
.add_node(dog_bark) \
.add_node(cat_mood) \
.add_node(cat_hide) \
.add_edge(Edge(season, allergies, EdgeType.DIRECTED)) \
.add_edge(Edge(season, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(season, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(atmos_pres, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, grass, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, dog_bark, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, cat_mood, EdgeType.DIRECTED)) \
.add_edge(Edge(dog_bark, cat_hide, EdgeType.DIRECTED)) \
.add_edge(Edge(cat_mood, cat_hide, EdgeType.DIRECTED))
Nous avons d’abord décrit nos nœuds avec des probabilités conditionnelles. Vous devriez remarquer que j’ai sauté certaines valeurs d’état possibles pour la simplicité. Par exemple, la variable saison prend d’autres valeurs « printemps » et « automne ». Donc, l’idée est la même.
Non, vérifions que notre réseau est construit correctement ou non.
with warnings.catch_warnings():
warnings.simplefilter('ignore')
graph = convert_for_drawing(bbn)
pos = nx.nx_agraph.graphviz_layout(graph, prog='neato')plt.figure(figsize=(20, 10))
plt.subplot(121)
labels = dict()
nx.draw(graph, pos=pos, with_labels=True, labels=labels)
plt.title('BBN DAG')
Ce bout de code donnerait le graphe suivant
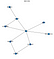
Donc, vous voyez que ce réseau correspond à mon dessin fantaisiste du début. Maintenant, faisons quelques inférences sur ce réseau de croyance.
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()join_tree.set_observation(ev)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
Ce bout de code donne essentiellement des preuves au réseau qui est la saison est l’hiver avec une probabilité de 1,0. Selon cette preuve, lorsque nous faisons l’inférence, nous obtenons les résultats suivants.
0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.80000
3=sunny|0.20000
--------------------->
4|grass|grass,no_grass
4=grass|0.70000
4=no_grass|0.30000
--------------------->
1|atmos_press|high,low
1=high|0.50000
1=low|0.50000
--------------------->
5|umbrellas|on,off
5=on|0.95200
5=off|0.04800
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.66000
6=not_bark|0.34000
--------------------->
7|cat_mood|good,bad
7=good|0.23000
7=bad|0.77000
--------------------->
8|cat_hide|hide,show
8=hide|0.87150
8=show|0.12850
--------------------->
Lorsque nous ajoutons d’autres preuves, comme le chien n’aboie pas
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()ev2 = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('dog_bark')) \
.with_evidence('not_bark', 1.0) \
.build()join_tree.set_observation(ev)
join_tree.set_observation(ev2)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
Nous obtenons les résultats d’inférence suivants
0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.47059
3=sunny|0.52941
--------------------->
4|grass|grass,no_grass
4=grass|0.53529
4=no_grass|0.46471
--------------------->
1|atmos_press|high,low
1=high|0.39706
1=low|0.60294
--------------------->
5|umbrellas|on,off
5=on|0.88941
5=off|0.11059
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.00000
6=not_bark|1.00000
--------------------->
7|cat_mood|good,bad
7=good|0.52647
7=bad|0.47353
--------------------->
8|cat_hide|hide,show
8=hide|0.83162
8=show|0.16838
--------------------->
Voyez-vous la différence ? 😆 Beaucoup de valeurs de probabilité ont changé lorsque nous avons ajouté la preuve liée à l’aboiement. C’est certainement un exemple idiot mais agréable pour avoir une intuition.
Comment utiliser les réseaux bayésiens dans SNA ?
Les réseaux bayésiens sont des outils très puissants pour comprendre la structure des relations de causalité entre les variables. Une fois que vous avez conçu votre modèle, même avec un petit ensemble de données, il peut vous dire diverses choses. La question dans cette partie est de savoir comment tirer profit des réseaux bayésiens dans le SCN. La réponse n’est pas unique, mais commençons par une idée profonde. Dans la SNA, nous essayons de comprendre la structure d’un réseau social. En outre, nous essayons de comprendre l’importance des nœuds. Mais nous ne savons pas quels sont les résultats de nos mesures d’importance. C’est à ce stade que les réseaux bayésiens interviennent. Par exemple, si vous pensez que l’importance d’un nœud est causée par la centralité de degré et la centralité de lien, vous pouvez avoir le réseau suivant.
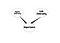
C’est un réseau bayésien très naïf. En plus de déterminer l’importance des nœuds, une autre application peut être la recherche d’un type spécifique de nœuds. Considérons un réseau social dans lequel il y a des personnes qui sont des leaders potentiels et je veux les rechercher. Considérons le graphe suivant
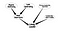
Ce réseau un peu plus compliqué nous aidera à déterminer l’incertitude des noeuds liés à un leadership.
Une autre application serait de déduire les liens. Les nouveaux liens peuvent être inférés à partir des liens existants. Par exemple, à partir de l’appartenance à un groupe dans un réseau social, le lien d’appartenance probable peut être inféré. Ce que je voulais dire, c’est que nous pouvons modéliser un nouveau lien entre les utilisateurs et les groupes en considérant les liens existants. Voir le diagramme de modèle suivant
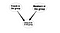
So, ce sont quelques exemples de base de la façon dont les réseaux bayésiens peuvent être appliqués dans le SNA. Ce sujet n’est pas très bien étudié mais je pense qu’il pourrait être très utile de l’étudier plus avant.
Conclusion
La chose difficile avec les réseaux bayésiens est la conception. En particulier, quand vous pensez à SNA, la construction de la cartographie du réseau social avec un réseau bayésien est l’art que la science 😃 Mais une fois que vous avez fait le travail d’art et conçu votre modèle très bien, ces outils pratiques peuvent vous dire beaucoup de choses. Comme nous le savons, les réseaux bayésiens sont appliqués dans de nombreux domaines. Ils ont très bien fonctionné dans la plupart des cas. Par conséquent, je crois fermement que nous pouvons faire des inférences très profondes sur les réseaux sociaux, aussi.
Pour de plus amples recherches avec SNA et les réseaux bayésiens, s’il vous plaît restez à l’écoute 🚀
.