La classification est une approche d’apprentissage automatique supervisée, dans laquelle l’algorithme apprend à partir de l’entrée de données qui lui est fournie – et utilise ensuite cet apprentissage pour classer de nouvelles observations.

En d’autres termes, l’ensemble de données d’entraînement est employé pour obtenir de meilleures conditions limites qui peuvent être utilisées pour déterminer chaque classe cible ; une fois que ces conditions limites sont déterminées, la tâche suivante consiste à prédire la classe cible.

Les classificateurs binaires travaillent avec seulement deux classes ou résultats possibles (exemple : sentiment positif ou négatif ; si le prêteur va payer le prêt ou non ; etc), et les classificateurs Multiclasses travaillent avec plusieurs classes (ex : à quel pays appartient un drapeau, si une image est une pomme ou une banane ou une orange ; etc). Multiclasse suppose que chaque échantillon est affecté à une et une seule étiquette.

L’un des premiers algorithmes populaires de classification en apprentissage automatique était Naive Bayes, un classificateur probabiliste inspiré du théorème de Bayes (qui nous permet de faire des déductions raisonnées d’événements se produisant dans le monde réel en fonction de la connaissance préalable d’observations qui peuvent l’impliquer). Le nom (« Naive ») provient du fait que l’algorithme suppose que les attributs sont conditionnellement indépendants.

L’algorithme est simple à mettre en œuvre et représente généralement une méthode raisonnable pour donner le coup d’envoi des efforts de classification. Il peut facilement s’adapter à des ensembles de données plus importants (il prend un temps linéaire par rapport à l’approximation itérative, utilisée pour de nombreux autres types de classificateurs, qui est plus coûteuse en termes de ressources de calcul) et nécessite une petite quantité de données d’entraînement.

Cependant, Naive Bayes peut souffrir d’un problème connu sous le nom de ‘ problème de probabilité zéro ‘, lorsque la probabilité conditionnelle est nulle pour un attribut particulier, ne fournissant pas une prédiction valide. Une solution consiste à exploiter une procédure de lissage (ex : méthode de Laplace).

P(c|x) est la probabilité postérieure de la classe (c, cible) étant donné le prédicteur (x, attributs). P(c) est la probabilité antérieure de la classe. P(x|c) est la vraisemblance qui est la probabilité du prédicteur étant donné la classe, et P(x) est la probabilité antérieure du prédicteur.

La première étape de l’algorithme consiste à calculer la probabilité antérieure pour des étiquettes de classe données. Puis de trouver la probabilité de vraisemblance avec chaque attribut, pour chaque classe. Par la suite, mettre ces valeurs dans la formule de Bayes & calculer la probabilité postérieure, puis voir quelle classe a une plus grande probablité, étant donné que l’entrée appartient à la classe de plus grande probabilité.

Il est assez simple d’implémenter Naive Bayes en Python en s’appuyant sur la bibliothèque scikit-learn. Il existe en fait trois types de modèle Naive Bayes sous la bibliothèque scikit-learn : (a) type gaussien (suppose que les caractéristiques suivent une distribution normale en forme de cloche), (b) multinomial (utilisé pour les comptages discrets, en termes de quantité de fois qu’un résultat est observé sur x essais), et (c) Bernoulli (utile pour les vecteurs de caractéristiques binaires ; le cas d’utilisation populaire est la classification de texte).

Un autre mécanisme populaire est l’arbre de décision. Étant donné une donnée d’attributs ainsi que ses classes, l’arbre produit une séquence de règles qui peuvent être utilisées pour classer les données. L’algorithme divise l’échantillon en deux ou plusieurs ensembles homogènes (feuilles) sur la base des différentiateurs les plus significatifs de vos variables d’entrée. Pour choisir un différenciateur (prédicteur), l’algorithme prend en compte toutes les caractéristiques et effectue une division binaire sur celles-ci (pour les données catégorielles, division par catégorie ; pour les données continues, choix d’un seuil de coupure). Il choisira ensuite celui qui a le moindre coût (c’est-à-dire la plus grande précision), en répétant récursivement, jusqu’à ce qu’il réussisse à diviser les données dans toutes les feuilles (ou qu’il atteigne la profondeur maximale).

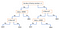
Les arbres de décision sont en général simples à comprendre et à visualiser, et nécessitent peu de préparation des données. Cette méthode peut également traiter des données numériques et catégorielles. D’un autre côté, les arbres complexes ne généralisent pas bien (« overfitting »), et les arbres de décision peuvent être quelque peu instables car de petites variations dans les données peuvent entraîner la génération d’un arbre complètement différent.

Une méthode de classification qui est dérivée des arbres de décision est la Random Forest, essentiellement un « méta-estimateur » qui ajuste un certain nombre d’arbres de décision sur divers sous-échantillons d’ensembles de données et utilise la moyenne pour améliorer la précision prédictive du modèle et contrôle l’over-fitting. La taille du sous-échantillon est la même que celle de l’échantillon d’entrée original – mais les échantillons sont tirés avec remplacement.

Les forêts aléatoires ont tendance à présenter un degré plus élevé de robustesse à l’overfitting (>robustesse au bruit dans les données), avec un temps d’exécution efficace même dans les grands ensembles de données. Elles sont cependant plus sensibles aux ensembles de données non équilibrés, étant aussi un peu plus complexes à interpréter et nécessitant plus de ressources informatiques.

Un autre classificateur populaire dans ML est la régression logistique – où les probabilités décrivant les résultats possibles d’un seul essai sont modélisées en utilisant une fonction logistique (méthode de classification malgré le nom):

Voici à quoi ressemble l’équation logistique :

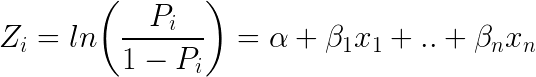
En prenant e (exposant) des deux côtés de l’équation, on obtient :

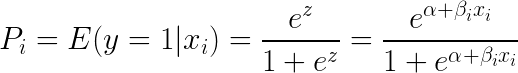
La régression logistique est plus utile pour comprendre l’influence de plusieurs variables indépendantes sur une seule variable de résultat. Elle est axée sur la classification binaire (pour les problèmes à classes multiples, on utilise des extensions de la régression logistique telles que la régression logistique multinomiale et ordinale). La régression logistique est populaire à travers les cas d’utilisation tels que l’analyse de crédit et la propension à répondre/acheter.

Enfin, le kNN (pour « k Nearest Neighbors ») est également souvent utilisé pour les problèmes de classification. Le kNN est un algorithme simple qui stocke tous les cas disponibles et classe les nouveaux cas en fonction d’une mesure de similarité (par exemple, les fonctions de distance). Il a été utilisé dans l’estimation statistique et la reconnaissance des formes dès le début des années 1970 comme technique non paramétrique :

.