Posted on

Phase (ondes)

, Author

La phase d’une oscillation ou d’une onde est la fraction d’un cycle complet correspondant à un décalage du déplacement par rapport à un point de référence spécifié au temps t = 0. La phase est un concept du domaine des fréquences ou du domaine de la transformée de Fourier, et en tant que tel, peut être facilement compris en termes de mouvement harmonique simple. Le même concept s’applique au mouvement ondulatoire, vu soit en un point de l’espace sur un intervalle de temps, soit à travers un intervalle d’espace à un moment donné. Le mouvement harmonique simple est un déplacement qui varie de façon cyclique, comme représenté ci-dessous :

File:Simple harmonic motion.png

et décrit par la formule:

{\displaystyle x(t)=A\cdot \sin(2\pi ft+\theta ),}

où A est l’amplitude de l’oscillation, f est la fréquence, t est le temps écoulé, et {\displaystyle \theta } est la phase de l’oscillation. La phase détermine ou est déterminée par le déplacement initial au temps t = 0. Un mouvement de fréquence f a une période {\displaystyle T={\frac {1}{f}}.}

Deux ambiguïtés potentielles peuvent être notées:

  • L’une est que le déplacement initial de {{displaystyle \cos(2\pi ft+\theta )\,} est différent de la fonction sinus, pourtant elles semblent avoir la même « phase ».
  • L’angle variant dans le temps {\displaystyle 2\pi ft+\theta ,\,} ou sa valeur modulo {\displaystyle 2\pi }, est aussi communément appelé « phase ». Il ne s’agit alors pas d’une condition initiale, mais plutôt d’une condition qui change continuellement.

Le terme phase instantanée est utilisé pour distinguer l’angle variant dans le temps de la condition initiale. Il a également une définition formelle qui est applicable à des fonctions plus générales et définit sans ambiguïté la phase initiale d’une fonction à t=0. C’est-à-dire que le sinus et le cosinus ont intrinsèquement des phases initiales différentes. En l’absence d’indication contraire explicite, le cosinus doit généralement être déduit. (voir aussi phasor)

Déplacement de phase

Fichier:Déplacement de phase.png

Illustration du déplacement de phase. L’axe horizontal représente un angle (phase) qui augmente avec le temps.

{\displaystyle \theta } est parfois appelé un déphasage, car il représente un « décalage » par rapport à la phase zéro. Mais un changement dans {\displaystyle \theta } est également appelé un déphasage.

Pour les sinusoïdes infiniment longues, un changement dans {\displaystyle \theta } est identique à un décalage dans le temps, tel qu’un retard. Si {\displaystyle x(t)\,} est retardé (décalé dans le temps) de {\displaystyle {\begin{matrix}{\frac {1}{4}}\end{matrix}}\,} de son cycle, il devient :

{\displaystyle x(t-{\begin{matrix}{\frac {1}{4}}\end{matrix}}T)},} {\displaystyle =A\cdot \sin(2\pi f(t-{\begin{matrix}{\frac {1}{4}}\end{matrix}}T)+\theta )\,}
{\displaystyle =A\cdot \sin(2\pi ft-{\begin{matrix}{\frac {\pi }{2}\end{matrix}}+\theta ),\,}

dont la « phase » est maintenant {\displaystyle \theta -{\begin{matrix}{\frac {\pi }{2}\end{matrix}.} Elle a été décalée de {\displaystyle {\begin{matrix}{\frac {\pi }{2}}\end{matrix}}.

Différence de phase

File:Sine waves same phase.svg

Ondes en phase

File:Sine waves different phase.svg

Out-of-phase waves

File:Phase-shift illustration.png

Gauche : la partie réelle d’une onde plane se déplaçant de haut en bas. A droite : la même onde après qu’une section centrale ait subi un déphasage, par exemple en traversant un verre d’épaisseur différente de celle des autres parties. (L’illustration de droite ignore l’effet de la diffraction dont l’effet augmente sur de grandes distances).

Deux oscillateurs qui ont la même fréquence et des phases différentes ont une différence de phase, et on dit que les oscillateurs sont déphasés entre eux. La quantité par laquelle de tels oscillateurs sont déphasés l’un par rapport à l’autre peut être exprimée en degrés de 0° à 360°, ou en radians de 0 à 2π. Si la différence de phase est de 180 degrés (π radians), on dit que les deux oscillateurs sont en antiphase. Si deux ondes en interaction se rencontrent en un point où elles sont en antiphase, alors des interférences destructives se produisent. Il est courant que des ondes électromagnétiques (lumière, RF), acoustiques (son) ou d’autres énergies se superposent dans leur milieu de transmission. Lorsque cela se produit, la différence de phase détermine si elles se renforcent ou s’affaiblissent mutuellement. Une annulation complète est possible pour des ondes d’amplitudes égales.

Le temps est parfois utilisé (au lieu de l’angle) pour exprimer la position dans le cycle d’une oscillation.

  • Une différence de phase est analogue à deux athlètes qui courent autour d’une piste de course à la même vitesse et dans la même direction, mais qui commencent à des positions différentes sur la piste. Ils passent devant un point à des instants différents dans le temps. Mais la différence de temps (différence de phase) entre eux est une constante – la même à chaque passage puisqu’ils sont à la même vitesse et dans la même direction. S’ils étaient à des vitesses différentes (fréquences différentes), la différence de phase ne ferait que refléter des positions de départ différentes.
  • Nous mesurons la rotation de la terre en heures, au lieu de radians. Et donc les fuseaux horaires sont un exemple de différences de phase.

Composantes en phase et en quadrature (I&Q)

Le terme en phase se retrouve également dans le contexte des signaux de communication:

{\displaystyle A(t)\cdot \sin=I(t)\cdot \sin(2\pi ft)+Q(t)\cdot \underbrace {\cos(2\pi ft)}. _{\sin \left(2\pi ft+{\begin{matrix}{\frac {\pi }{2}}\end{matrix}}\right)}

et:

{\displaystyle A(t)\cdot \cos=I(t)\cdot \cos(2\pi ft)\underbrace {-Q(t)\cdot \sin(2\pi ft)} _{+Q(t)\cdot \cos \left(2\pi ft+{\begin{matrix}{\frac {\pi }{2}}\end{matrix}}\right)}

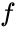
où {{displaystyle f\,} représente une fréquence porteuse, et

{\displaystyle I(t)\ {\stackrel {\mathrm {def} }{=}\ A(t)\cdot \cos,\,}{\displaystyle Q(t)\ {\stackrel {\mathrm {def} }{=}\ A(t)\cdot \sin.\,}

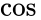
{\displaystyle A(t)\,} et {\displaystyle \phi (t)\,} représentent la modulation possible d’une onde porteuse pure, par exemple : {\displaystyle \sin(2\pi ft).\,} La modulation modifie la composante originale {\displaystyle \sin \,} de la porteuse, et crée une (nouvelle) {\displaystyle \cos \,} composante, comme indiqué ci-dessus. La composante qui est en phase avec la porteuse d’origine est appelée la composante en phase. L’autre composante, qui est toujours à 90° ({\displaystyle {\begin{matrix}{\frac {\pi }{2}}\end{matrix}}} radians) « déphasée », est appelée composante en quadrature.

Cohérence de phase

La cohérence est la qualité d’une onde à afficher une relation de phase bien définie dans différentes régions de son domaine de définition.

En physique, la mécanique quantique attribue des ondes aux objets physiques. La fonction d’onde est complexe et comme son module carré est associé à la probabilité d’observer l’objet, le caractère complexe de la fonction d’onde est associé à la phase. L’algèbre complexe étant responsable de l’effet d’interférence frappant de la mécanique quantique, la phase des particules est donc finalement liée à leur comportement quantique.

Laisser un commentaire

Votre adresse e-mail ne sera pas publiée.