(IUCr) Symboles des éléments de symétrie

Acta Cryst. (1992). A48, 727-732

Rapport final du comité ad hoc de l’Union internationale de cristallographie sur la nomenclature de la symétrie*

Par P. M. DE WOLFF (président), Meermanstraat 126, 2614 AM Delft, Pays-Bas,

Y. BILLIET, Ecole Nationale d’Ingénieurs, BPW 3038 Sfax, Tunesië,

J. D. H. DONNAY, Département des sciences géologiques, Université McGill, 3450, rue University, Montréal, Canada H3A 2A7,

W. FISCHER, Institut für Mineralogie, Petrologie und Kristallographie der Phillips-Universität, Lahnberge, D-3550 Marburg (Lahn), Allemagne,

R. B. GALIOULINE, Institut de cristallographie, Académie des sciences de Russie, Leninsky Prospekt 59, Moscou 117333, Russie,

A. M. GLAZER, Clarendon Laboratory, Université d’Oxford, Parks Road, Oxford OX1 3PU Angleterre,

TH. HAHN, Institut für Kristallographie, RWTH, Templergraben 55, D-5100 Aachen, Allemagne,

MARJORIE SENECHAL, Département de mathématiques, Smith College, Northampton, MA 01063, USA,

D. P. SHOEMAKER, Département de chimie, Université d’Etat de l’Oregon, OR 97331, USA,

H. WONDRATSCHEK, Institut für Kristallographie, Universität Karlsruhe, Kaiserstrasse 12, D-7500 Karlsruhe 1, Allemagne,

A. J. C. WILSON (ex officio, IUCr Commission on International Tables), Crystallographic Data Centre, University Chemistry Laboratory, Lensfield Road, Cambridge CB2 1EW, England

ET S. C. ABRAHAMS (ex officio, IUCr Commission on Crystallographic Nomenclature), Department of Physics, Southern Oregon State College, 1250 Siskiyou Boulevard, Ashland, OR 97520-5047, USA

(Reçu le 7 novembre 1991 ; accepté le 9 mars 1992)

* Nommé le 14 novembre 1984, modifié le 10 août 1987 selon les règles de base décrites dans Acta Cryst. (1979), A35, 1072. Rapport final accepté le 23 décembre 1991 par la Commission de la nomenclature cristallographique de l’UICR et le 9 mars 1992 par le Comité exécutif.

Abstract

Des symboles imprimés nouveaux ou redéfinis sont proposés à la lumière de la redéfinition récemment acceptée des éléments de symétrie . En particulier, la lettre e couvre certains plans de glissement qui, jusqu’à présent, n’avaient pas de symbole unique, comme ceux appelés « soit a, soit b ». L’utilisation de e dans le symbole d’Hermann-Mauguin de cinq groupes d’espace différents est recommandée. Pour les plans e projetés dans une direction parallèle au plan, un symbole graphique est proposé pour lever l’ambiguïté de leur désignation actuelle. La lettre k est proposée pour une classe nouvellement définie de plans de glissement qui, jusqu’à présent, n’avaient pas de symbole spécifique. Les symboles des opérations de symétrie introduits dans les descriptions des groupes d’espace des Tables internationales de cristallographie (1989), vol. A (Dordrecht : Kluwer Academic Publishers) sont recommandés pour une utilisation générale, avec des modifications uniquement pour les opérations de réflexion de glissement.

Introduction

Le comité ad hoc nommé en 1980 pour examiner les « problèmes de nomenclature concernant les opérations de symétrie et les éléments de symétrie dans les groupes d’espace » a publié deux rapports intitulés Nomenclature des familles de cristaux, types de réseaux de Bravais et classes arithmétiques (de Wolff et al, 1985) et Definition of Symmetry Elements in Space Groups and Point Groups (de Wolff et al., 1989). Comme indiqué dans le rapport de 1989, le seul problème en suspens concernant les opérations de symétrie est celui du choix des symboles appropriés, puisque le concept est clair. Une notation provisoire a été adoptée dans les Tables internationales de cristallographie (1983, 1989), désignées ci-après par ITA83.

Symboles imprimés pour les éléments de symétrie

La définition des éléments de symétrie telle qu’elle est donnée dans le Rapport 1989 (de Wolff et al.) sera utilisée tout au long du présent Rapport. Nous en répétons ici l’essentiel :

Pour toute opération de symétrie donnée, son élément géométrique (plan, point et/ou ligne) est défini. Un élément de symétrie est la combinaison de l’élément géométrique de l’une des opérations de symétrie dans un groupe d’espace donné avec l’ensemble (appelé `ensemble d’éléments’) de toutes les opérations de symétrie dans ce groupe d’espace qui partagent cet élément géométrique.

Les définitions explicites des éléments géométriques et les descriptions des éléments de symétrie qui en découlent ainsi que leurs symboles sont donnés dans les tableaux 1 et 2. (Ils sont identiques aux tableaux 1 et 2 du Rapport de 1989 sauf pour les plans de glissement et sont répétés ici pour être complets, voir ci-dessous). Chaque élément de symétrie est représenté par un symbole composé de deux caractères. Le premier caractère est un E majuscule pour tous les éléments de symétrie. Il sert à montrer que le symbole se réfère à un élément de symétrie et non, par exemple, à une opération de symétrie. Si cela est déjà clair d’après le contexte, alors le E peut être omis, par exemple « un axe 2 » au lieu de « un axe E2 ».

Tableau 1. Éléments géométriques des opérations de symétrie dans les groupes de points et les groupes d’espace
Opération de symétrie	Élément géométrique	Paramètres supplémentaires
Identity	Non requis	None
Translation	Non requis	Vecteur $\mathbf{t}$ .
Réflexion dans le plan A	Plan A	Non
Réflexion du glissement =réflexion dans le plan A et translation. $\mathbf{v}$ parallèle à A	Plan A	Vecteur de glissement $\mathbf{v}$
Rotation autour de la ligne b	Ligne b	Angle et sens de rotation
Rotation de la vis = rotation autour de la ligne b et translation $\mathbf{u}$ parallèle à b	Ligne b	Angle et sens du vecteur vis de rotation $\mathbf{u}$
Rotoinversion = rotation autour de la ligne b et inversion par le point P sur b	Ligne b et point P sur b	Angle (non égal à $\pi$ ) et sens de rotation
Inversion par le point P	Point P	Non

Le symbole Eg énuméré dans le rapport de 1989 peut être utilisé pour les plans de glissement si l’on veut simplement montrer que l’élément de symétrie est un plan de glissement. En revanche, s’il appartient à l’un des types spéciaux qui sont depuis longtemps désignés par une lettre appropriée (a, b, c, n ou d ; cf. ITA83), alors cette lettre remplace g dans Eg.

Tableau 2. Éléments de symétrie dans les groupes de points et les groupes d’espace
Nom de l’élément de symétrie	Symbole	Élément géométrique	Opération de définition (d.o.)	Opérations dans l’ensemble des éléments
Plan miroir	Em	Plan A	Réflexion dans A	D.o. et ses équivalents coplanaires*
Plan de glissement	Eg $\ddag$	Plan A	Réflexion de glissement dans A, 2v (pas v) une translation de treillis	D.o.. et ses équivalents coplanaires*
Axe de rotation	En	Ligne b	Rotation autour de b, angle $2\pi/n$ ,n = 2, 3, 4 ou 6	1ère, $\dots$ ,(n – 1)ème puissances de d.o.. et leurs équivalents coaxiaux $\dag$
Axe de la vis	Enj	Ligne b	Rotation de la vis autour de b, angle $2\pi/n$ , u =j/n fois le plus court réseau translation le long de b, vis droite ; n = 2, 3, 4 ou 6, $j=1,\dots,(n-1)$	1ère, $\dots$ ,(n – 1)ème puissances de d.o. et leurs équivalents coaxiaux $\dag$
Axe de rotoinversion	$E\bar n$	Ligne b et point P sur b	Rotoinversion : rotation autour de b, angle $2\pi/n$ , et inversion par P ; n = 3, 4 ou 6	D.o. et son inverse
Centre	$E\bar 1$	Point P	Inversion par P	D.o. seulement

* C’est-à-dire toutes les réflexions glissantes avec le même plan de réflexion, avec des vecteurs de glissement différant de celui du d.o. (pris comme nul pour une réflexion) par un vecteur de translation du treillis.
$\dag$ C’est-à-dire toutes les rotations et rotations de vis avec le même axe b, le même angle et le même sens de rotation et le même vecteur de vis $\mathbf{u}$ (nul pour une rotation) jusqu’à un vecteur de translation de treillis.
$\ddag$ En Eg, g est remplacé par a, b, c, n, d, e ou k pour des types spécifiques de plans de glissement, cf. §2.

Un nouvel aspect important des symboles comme Eb peut cependant être souligné. Selon l’ITA83, dénoter un plan par b signifiait simplement qu’une réflexion de glissement dans le plan avec une composante de glissement b/2 le long de l’axe b est une opération de symétrie. Cette définition s’applique certainement à la situation représentée sur la figure 1.

Fig. 1. (D’après W. Fischer.) L’ensemble des éléments d’un plan de glissement Eb, représenté comme un ensemble de points au-dessus (+) et au-dessous (-) du plan produits par des réflexions de glissement dans le plan, en partant par exemple du signe + en haut à gauche. Le réseau N des translations parallèles au plan (+ $\cdots$ + vecteurs) est indiqué par une maille, qui dans ce cas se trouve être rectangulaire. Les deux paires de bords sont parallèles aux axes du cristal. Il y a une réflexion de glissement avec son vecteur de glissement (+ $\cdots$ -) le long de l’axe b.

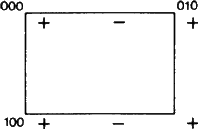
$\begin{figure} \includegraphics {fig1.ps} \end{figure}$

La figure 1 est adaptée, comme les figures 2 et 3, d’un ensemble de figures similaires conçues par W. Fischer, membre du comité ad hoc, comme un inventaire de tous les types de plan de descente. Bien que cet ensemble ait été présenté au Comité en 1980, bien avant la publication du rapport de 1989, chacune de ses figures montre précisément l' »ensemble d’éléments » du plan de descente tel que défini dans ce rapport (cf. le résumé ci-dessus). Pour un plan de glissement, l’ensemble des éléments est constitué de toutes les réflexions de glissement ayant le plan comme élément géométrique commun. Leur action est représentée en projection sur ce plan. À partir de la position de départ de tout signe +, chaque signe – résulte de l’une des réflexions glissantes de l’ensemble. Tout cela est représenté dans un maillage élémentaire du motif périodique bidimensionnel résultant des signes + et -.

Nous ferons souvent référence au filet N formé par toutes les translations parallèles au plan ; ce filet est facilement visualisable en regardant uniquement les signes +. Ces vecteurs sont à distinguer nettement des vecteurs reliant un signe + à un signe – quelconque, chacun d’eux étant le vecteur de glissement d’une réflexion de glissement appartenant à l’ensemble des éléments.

Le nouvel aspect apparaît parce que, dans certains cas, par la définition de l’ITA83, le plan de glissement b est aussi un plan de glissement a ; voir la figure 2. Il est clair que cela ne se produit que si le filet N est centré orthogonalement, car alors le glissement a peut être transformé en glissement b (et vice versa) en ajoutant une translation de centrage. Jusqu’à présent, la pratique a consisté à appeler un tel plan de glissement arbitrairement soit a soit b, ce qui entraîne un biais injustifié et un manque d’unicité de ces symboles. Par conséquent, nous proposons que le cas de la figure 2 soit couvert par un symbole distinct.

Fig. 2. (D’après W. Fischer.) L’ensemble des éléments d’un plan Ee-glide. Cf. la légende de la figure 1. Noter que le filet N est ici centré orthogonalement.

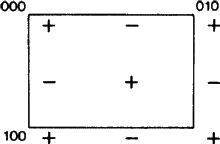
$\begin{figure} \includegraphics {fig2.ps} \end{figure}$

La portée de ce symbole devrait alors être étendue aux plans de glissement dans une orientation diagonale, c’est-à-dire parallèle à un seul axe cristallin, à condition que le plan de glissement ait un vecteur de glissement le long de cet axe et que le net N soit centré orthogonal. Pour de tels plans, il n’y a pas l’ambiguïté du choix aléatoire a-b ci-dessus, mais la portée étendue du nouveau symbole est conforme à celle de tous les symboles existants (à savoir a, b, c, n et d). Chacun d’entre eux est utilisé pour un plan de glissement avec à la fois un et deux axes cristallins dans le réseau N, cf. Fig. 3.

La lettre e est proposée pour le nouveau symbole. Ainsi, Ee s’appliquera aux plans de glissement avec des filets centrés orthogonaux N et au moins un vecteur de glissement le long d’un axe cristallin. Un nouveau critère est donc nécessaire : l’orientation des vecteurs de glissement par rapport aux axes conventionnels du cristal. Comme ces derniers suivent les directions de symétrie, alors que chaque plan de glissement est parallèle à un plan miroir du réseau, il n’est pas surprenant qu’il y ait toujours au moins un axe conventionnel du cristal dans N. S’il n’y a qu’un seul axe de ce type, alors perpendiculairement à celui-ci, il y a toujours une autre translation dans N.

Le nouveau symbole e ainsi que les anciens symboles a, b, c, d, n seront maintenant redéfinis en fonction de ce nouveau critère et du type bravais du réseau N. Ce réseau est monoclinique ou orthogonal ou tétragonal primitif (mp ou op ou tp) ou orthogonal centré (oc). Seuls les filets N de type oc permettent un plan de glissement Ee. Le symbole En s’applique aux réseaux N de type bravais mp ou op, tandis que Ed s’applique aux réseaux N de type oc. (Comme indiqué dans une note de bas de page du tableau 1.3 de l’ITA83 : « Les plans de glissement d n’apparaissent que dans les groupes d’espace F orthorhombique, dans les groupes d’espace I tétragonal et dans les groupes d’espace I et F cubique. Ils apparaissent toujours par paires avec des vecteurs de glissement alternés’). Contrairement aux plans Ea, Eb, Ec et Ee, cependant, pour les plans En et Ed, il n’y a pas de vecteur de glissement parallèle ou perpendiculaire à un axe conventionnel dans N.

Les définitions qui s’ensuivent des plans de glissement des types ci-dessus sont résumées dans les lignes (i) et (ii) du tableau 3, et plus explicitement dans la figure 3.

Tableau 3. Symboles imprimés pour les types spéciaux de planeurs
Nombre de vecteurs de glissement parallèles ou perpendiculaires aux axes cristallins dans le réseau N	Type de réseau Bravais N
Le symbole est déterminé par deux critères. Le premier critère est le type Bravais (mp, op, tp ou oc) du filet N formé par les translations de symétrie parallèles au plan considéré. Ce filet contient toujours au moins un axe conventionnel du cristal.* L’autre critère se réfère à l’orientation des vecteurs de glissement par rapport à ces axes.
	m, op, tp	oc
(i) Un ou deux parallèles	Ec(Ea, Eb)	Ee
(ii) Aucun parallèle, aucun perpendiculaire	En	Ed
(iii) Aucun parallèle, un perpendiculaire	Ek	–

* Comme défini dans ITA83, § 9.1 ; cependant, pour les groupes d’espace rhomboédriques, on utilise ici uniquement les axes hexagonaux.

Tous les plans de glissement restants étaient auparavant sans symbole spécifique. Ils ont chacun une orientation diagonale (un seul axe cristallin conventionnel dans le réseau N). Parmi les réflexions de glissement dans leur ensemble d’éléments, il n’y en a aucune avec un vecteur de glissement le long de cet axe. Cependant, un vecteur de glissement est (par symétrie) perpendiculaire à cet axe. Un symbole semble souhaitable, aussi une nouvelle lettre est proposée : k. Le nouveau symbole Ek est brièvement défini à la ligne (iii) du tableau 3 et est entièrement illustré dans le bloc inférieur de la figure 3. Quelques exemples sont donnés dans le §2.

Fig. 3. (Adapté des dessins de W. Fisher.) Tous les aspects possibles des ensembles d’éléments des plans de glissement représentés comme dans la figure 1, mais indépendamment des étiquettes des axes. Les diagrammes sont regroupés en colonnes avec en tête le symbole de type réseau de Bravais (ligne supérieure) de leurs réseaux N, cf. tableau 3. Les autres critères de ce tableau sont vérifiés en regardant d’abord les doubles lignes indiquant les directions des axes des cristaux dans le plan. Un bord (vertical) du réseau N représenté est toujours choisi le long d’un tel axe. L’autre bord est horizontal sauf dans (1) et (8). Pour les diagrammes (1), $\dots$ ,(5), le symbole du plan de glissement est l’étiquette a, b ou c de l’axe vertical ; pour les autres, c’est la lettre encerclée dans le bloc ébauché contenant le diagramme. Notez les vecteurs de glissement verticaux dans les diagrammes (1), $\dots$ ,(7), les horizontaux dans (6), (7), (14), (15) et l’absence de l’un ou l’autre dans (8), $\dots$ ,(13). Un exemple d’occurrence est donné sous chaque diagramme par le symbole du groupe d’espace et le triplet de coordonnées du plan.

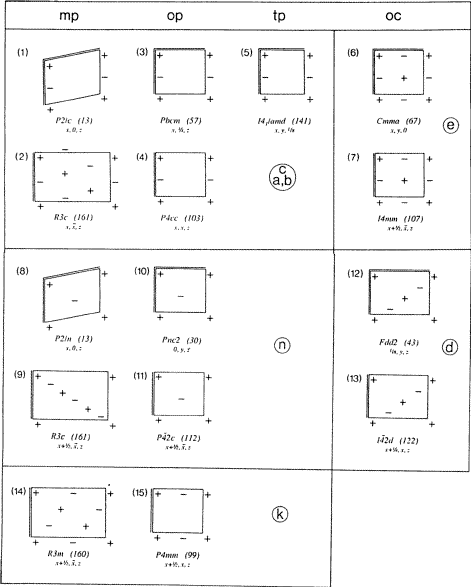
$\begin{figure} \includegraphics {fig3.ps} \end{figure}$

Dans la figure 3, l’inventaire de Fischer de tous les types de plan de glissement est présenté de manière abrégée – bien que toujours complète – dans laquelle une plus grande proéminence graphique a été donnée aux axes cristallins. Pour chaque diagramme, un exemple de son occurrence dans un groupe d’espace est listé.

Dans certains groupes d’espace rhomboédrique, des plans Ec, En et Ek orientés diagonalement apparaissent avec des réseaux de type mp N qui peuvent être décrits par un triple centrage d’un réseau orthogonal. Une triple maille rectangulaire du réseau N est représentée pour ces types de plans de glissement sur la figure 3, diagrammes (2), (9) et (14). On reconnaît la similitude avec d’autres diagrammes n tels que (8) ou (10) si dans le diagramme (9) on considère une maille primitive monoclinique du filet N avec des vecteurs de glissement diagonaux.

Symboles graphiques pour les éléments de symétrie

Les symboles graphiques existants tels que définis et utilisés dans l’ITA83 sont considérés comme adéquats par le comité ad hoc à une exception près. La situation est très différente de celle des symboles imprimés car, dans les dessins, la direction de projection devient un paramètre supplémentaire. Dans les termes « projection perpendiculaire » et « projection parallèle » utilisés ci-dessous, perpendiculaire et parallèle font référence à l’orientation de la direction de projection par rapport au plan de glissement.

Pour un plan Ee, le symbole 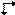existe pour sa projection perpendiculaire. Les symboles graphiques existants pour la projection parallèle d’un plan de glissement Ee- souffrent cependant de la même ambiguïté que les symboles imprimés. Ils expriment le vecteur glissement soit parallèlement soit perpendiculairement à la direction de projection, mais le choix est arbitraire. Par conséquent, un nouveau symbole est proposé pour la projection parallèle d’un plan de glissement Ee, à savoir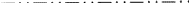

Exemples de plans Ee.

Tous les plans de glissement parallèles à deux axes des groupes d’espace Fmm2, Fmmm, $Fm\bar 3$ , $Fm\bar 3m$ et $Fm\bar 3c$ (n° 42, 69, 202, 225 et 226), ainsi que certains plans des cinq groupes d’espace énumérés au §3.

Des plans Ee orientés diagonalement apparaissent dans les groupes d’espace I4mm, I4cm, $I\bar 42m$ , I4/mmm, I4/mcm, $I\bar 43m$ et $Im\bar 3m$ (Nos. 107, 108, 121, 139, 140, 217 et 229).

Dans l’ITA83, tous ces plans Ee sont dessinés assez arbitrairement sous forme de lignes en pointillés ou en tirets dans leurs projections parallèles. La figure 4 montre le diagramme du groupe d’espace I4cm (n° 108), à la fois tel qu’il apparaît dans ITA83 et avec l’utilisation du nouveau symbole.

Fig. 4. (a) Diagramme du groupe d’espace I4cm (n° 108) tiré d’ITA83. (b) Idem, modifié par l’utilisation du symbole graphique proposé au § 2, pour la projection parallèle d’un plan Ee.

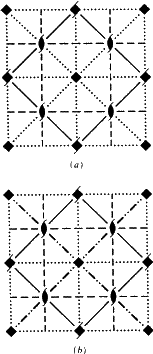
$\begin{figure} \includegraphics {fig4.ps} \end{figure}$

Bien que Ek soit un nouveau symbole d’impression, dans les diagrammes de l’ITA83 tous les plans de glissement Ek ont été dessinés de manière satisfaisante avec les mêmes conventions que celles utilisées pour les plans de glissement Ea/b/c. Comme dans ces cas, il existe un seul vecteur de glissement spécial (perpendiculaire à l’axe du cristal dans le réseau N, cf. tableau 3). Lorsque ce vecteur est, par exemple, parallèle au plan de projection, le plan Ek est toujours dessiné comme la ligne pointillée prescrite par la convention pertinente. Par conséquent, aucun nouveau symbole graphique n’est proposé pour les plans de glissement Ek.

Exemples de plans Ek.

De tels plans se retrouvent facilement dans les diagrammes de l’ITA83 comme plans parallèles à un seul axe et projetés en pointillés, par exemple xxz dans P4bm et $P\bar 42_1m$ (n° 100 et 113). En particulier, le tableau 3 est exactement conforme à la distinction indiquée entre les plans Ek et En. Voir, par exemple, les lignes en pointillés et en tirets pour R3m et R3c (n° 160 et 161).

Symboles de groupe d’espace d’Hermann-Mauguin

Les caractères apparaissant après la lettre de treillis dans le symbole d’Hermann-Mauguin (HM) d’un groupe d’espace étaient à l’origine destinés à représenter des opérations génératrices du groupe. Par exemple, b était une réflexion b-glide dans un plan orienté selon sa position dans le symbole HM.

En pratique, les éléments de symétrie populaires bien que mal définis ont pris le relais des opérations. Ainsi, b en est venu à être considéré comme un plan de glissement, Eb dans notre terminologie actuelle. Il n’y a aucun mal à cette réinterprétation, sauf lorsque l’opération appartient à un plan de glissement Ee. Si c’est le cas, par exemple, pour la réflexion b-glide ci-dessus, alors il existe un plan Ee mais pas de plan Eb-glide dans l’orientation correspondante. Dans ce cas, b devient un caractère très trompeur. En dehors de cela, le biais (donné à b par rapport à a ou c) est tout aussi perturbant que dans le cas des symboles d’éléments de symétrie traités au §1.

C’est pourquoi, il est proposé de remplacer ces lettres trompeuses a ou b par e dans les cinq symboles HM dans lesquels elles apparaissent :

Groupe spatial n°.	39	41	64	67	68
Symbole dans ITA83 :	Abm2	Aba2	Cmca	Cmma	Ccca
Nouveau symbole:	Aem2	Aea2	Cmce	Cmme	Ccce.

Un autre avantage des nouveaux symboles proposés est que e – contrairement à a ou b – est neutre et n’est donc pas modifié lors de la permutation des axes.

Symboles imprimés pour les opérations de symétrie

Un ensemble complet de symboles imprimés a été conçu par W. Fischer & E. Koch (ITA83, §11.2) et a été largement appliqué dans les sections sur les opérations de symétrie des descriptions des groupes spatiaux.

En bref, chaque symbole se compose d’un maximum de trois parties. La première partie est un caractère unique (parfois avec un indice) qui décrit le type d’opération. La ou les parties suivantes donnent les composantes de tout vecteur de déplacement ou de translation pertinent – toujours entre parenthèses – et les coordonnées de l’élément géométrique de l’opération, dans cet ordre.

Le comité ad hoc, après avoir examiné ce système, souhaite introduire deux modifications pour les réflexions de glissement :

(i) au lieu du premier caractère actuel (qui peut être a, b, c, n, d ou g), toujours écrire la lettre g ;

(ii) toujours écrire les composantes du vecteur de glissement (entre parenthèses) en entier, en particulier pour les réflexions de glissement simples dans les plans de glissement a, b ou c où elles étaient précédemment omises.

La règle (i) supprime l’information sur le type de plan de glissement auquel appartient l’opération. Très souvent, cette information n’est pas pertinente, voire prête à confusion. Pour les plans a/b/c, la suppression peut détruire des informations essentielles, mais la perte est rétablie par la règle (ii) comme le montre l’exemple ci-dessous.

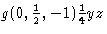En adoptant ces changements, l’uniformité des symboles – également en ce qui concerne ceux des rotations – est grandement améliorée. Par exemple, le symbole de la réflexion glissante dans le plan $x = \frac{1}{4}$ , avec le vecteur glissant inhabituel $(0, \frac{1}{2}, -1)$ , à savoir $g(0, \frac{1}{2}, 1) \frac{1}{4}yz$ , s’aligne maintenant sur celui d’une simple réflexion b-glissante. Dans l’ITA83, cette dernière était désignée par $b \frac{1}{4} y z$ , mais elle est transformée par la règle (ii) en $g(0, \frac{1}{2}, 0) \frac{1}{4} y z$ .

Les règles ci-dessus s’appliquent également aux réflexions glissantes appartenant à l’ensemble des éléments d’un plan miroir. Ainsi, si la composante de décalage d’une telle opération est (0, 1, 2), alors son symbole commence par g(0, 1, 2), et non par m(0, 1,2).

Tables internationales de cristallographie (1983). Vol. A, édité par TH. HAHN, notamment les §§ 1.1, 1.3, 1.4, 7 et 11. Dordrecht : Kluwer Academic Publishers.

Tables internationales de cristallographie (1989). Vol. A, 2e, révisé, ed., édité par TH. HAHN. Dordrecht : Kluwer Academic Publishers.

WOLFF, P. M. DE, BELOV, N. V., BERTAUT, E. F., BUERGER, M. J., DONNAY, J. D. H., FISCHER, W., HAHN, TH., KOPTSIK, V. A., MACKAY, A. L., WONDRATSCHEK, H., WILSON, A. J. C. & ABRAHAMS, S. C. (1985). Acta Cryst. A41, 278-280.

WOLFF, P. M. DE, BILLIET, Y., DONNAY, J. D. H., FISCHER, W., GALIULIN, R. B., GLAZER, A. M., SENECHAL, M., SHOEMAKER, D. P., WONDRATSCHEK, H., HAHN, TH., WILSON, A. J. C. & ABRAHAMS, S. C. (1989). Acta Cryst. A45, 494-499.

…vecteurs. Les symboles de plan de glissement c, n et k pour les trois diagrammes (2), (9) et (14) de la figure 3 ont bien sûr été attribués selon le tableau 3. Un membre de la commission ad hoc (le professeur Wondratschek) pense que le symbole n pour le diagramme (9) est en contradiction avec les notions traditionnelles concernant les plans n. Il propose l’attribution d’un symbole spécial pour les plans de glissement c et k. Il propose l’attribution d’un symbole spécial au diagramme (9). Cette proposition n’a cependant pas reçu un soutien suffisant au sein du Comité ad hoc.

Symboles des éléments de symétrie et des opérations de symétrie