Dans cet article, je vais expliquer comment les convolutions 2D sont mises en œuvre sous forme de multiplications matricielles. Cette explication est basée sur les notes du cours CS231n Réseaux neuronaux convolutifs pour la reconnaissance visuelle (module 2). Je suppose que le lecteur est familier avec le concept d’une opération de convolution dans le contexte d’un réseau neuronal profond. Si ce n’est pas le cas, ce repo contient un rapport et d’excellentes animations expliquant ce que sont les convolutions. Le code pour reproduire les calculs dans cet article peut être téléchargé ici.
Petit exemple
Supposons que nous ayons une image 4 x 4 à canal unique, X, et que ses valeurs de pixels soient les suivantes :

Supposons en outre que nous définissions une convolution 2D avec les propriétés suivantes :

Cela signifie qu’il y aura 9 patchs d’image 2 x 2 qui seront multipliés par éléments avec la matrice W, comme suit :

Ces patchs d’images peuvent être représentés comme des vecteurs colonnes à 4 dimensions et concaténés pour former une seule matrice 4 x 9, P, comme suit :

Notez que la i-ème colonne de la matrice P est en fait le i-ème patch d’image sous forme de vecteur colonne.
La matrice des poids pour la couche de convolution, W, peut être aplatie en un vecteur ligne à 4 dimensions , K, comme suit :
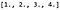
Pour effectuer la convolution, on multiplie d’abord matriciellement K par P pour obtenir un vecteur ligne à 9 dimensions (matrice 1 x 9) ce qui nous donne :

Puis nous remodelons le résultat de K P à la forme correcte, qui est une matrice 3 x 3 x 1 (dimension de canal en dernier). La dimension du canal est 1 parce que nous avons défini les filtres de sortie à 1. La hauteur et la largeur est 3 parce que selon les notes de CS231n:

Ce qui signifie que le résultat de la convolution est :
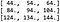
Ce qui se vérifie si nous exécutons la convolution en utilisant les fonctions intégrées de PyTorch (voir le code d’accompagnement de cet article pour plus de détails).
Exemple plus grand
L’exemple de la section précédente suppose une seule image et les canaux de sortie de la convolution sont 1. Qu’est-ce qui changerait si nous relâchions ces hypothèses ?
Supposons que notre entrée pour la convolution est une image 4 x 4 avec 3 canaux avec les valeurs de pixel suivantes :

Pour ce qui est de notre convolution, nous la définirons pour qu’elle ait les mêmes propriétés que la section précédente, sauf que ses filtres de sortie sont 2. Cela signifie que la matrice de poids initiale, W, doit avoir la forme (2, 2, 2, 3) c’est-à-dire (filtres de sortie, hauteur du noyau, largeur du noyau, canaux de l’image d’entrée). Définissons W comme ayant les valeurs suivantes :

Notez que chaque filtre de sortie aura son propre noyau (c’est pourquoi nous avons 2 noyaux dans cet exemple) et le canal de chaque noyau est 3 (puisque l’image d’entrée a 3 canaux).
Puisque nous sommes toujours en train de convoluer un noyau 2 x 2 sur une image 4 x 4 avec 0 zero-padding et stride 1, le nombre de patches d’image est toujours de 9. Cependant, la matrice de patchs d’image, P, sera différente. Plus précisément, la i-ème colonne de P sera la concaténation des valeurs des 1er, 2ème et 3ème canaux (sous forme de vecteur colonne) correspondant au patch d’image i. P sera maintenant une matrice 12 x 9. Les lignes sont 12 parce que chaque patch d’image a 3 canaux et chaque canal a 4 éléments puisque nous avons fixé la taille du noyau à 2 x 2. Voici à quoi ressemble P :

Comme pour W, chaque noyau sera aplati en un vecteur ligne et concaténé rangée par rangée pour former une matrice 2 x 12, K. La i-ème ligne de K est la concaténation des valeurs des 1er, 2ème et 3ème canaux (sous forme de vecteur de ligne) correspondant au i-ème noyau. Voici à quoi ressemblera K :

Maintenant, il ne reste plus qu’à effectuer la multiplication matricielle K P et à lui redonner la forme correcte. La forme correcte est une matrice 3 x 3 x 2 (dimension du canal en dernier). Voici le résultat de la multiplication :

Et voici le résultat après remodelage en une matrice 3 x 3 x 2 :

Ce qui se vérifie encore une fois si nous pour effectuer la convolution en utilisant les fonctions intégrées de PyTorch (voir le code d’accompagnement de cet article pour les détails).
So What?
Pourquoi devrions-nous nous soucier d’exprimer les convolutions 2D en termes de multiplications de matrices ? En plus de disposer d’une implémentation efficace adaptée à une exécution sur un GPU, la connaissance de cette approche nous permettra de raisonner sur le comportement d’un réseau de neurones convolutifs profonds. Par exemple, He et. al. (2015) ont exprimé les convolutions 2D en termes de multiplications de matrices, ce qui leur a permis d’appliquer les propriétés des matrices/vecteurs aléatoires pour argumenter en faveur d’une meilleure routine d’initialisation des poids.
Conclusion
Dans cet article, j’ai expliqué comment effectuer des convolutions 2D à l’aide de multiplications de matrices en parcourant deux petits exemples. J’espère que cela est suffisant pour vous permettre de généraliser à des dimensions d’image d’entrée et des propriétés de convolution arbitraires. Faites-moi savoir dans les commentaires si quelque chose n’est pas clair.
Convolution 1D
La méthode décrite dans cet article se généralise également aux convolutions 1D.
Par exemple, supposons que votre entrée est un vecteur 12-dimensionnel à 3 canaux comme ceci :

Si nous réglons notre convolution 1D pour avoir les paramètres suivants :
- taille du noyau : 1 x 4
- canaux de sortie : 2
- stride : 2
- padding : 0
- bias : 0
Alors les paramètres de l’opération de convolution, W, seront un tenseur de forme (2 , 3, 1, 4). Fixons W aux valeurs suivantes:

Selon les paramètres de l’opération de convolution, la matrice des patchs « image » P, aura une forme (12, 5) (5 patchs image où chaque patch image est un vecteur 12-D puisqu’un patch a 4 éléments à travers 3 canaux) et ressemblera à ceci :

Puis, on aplatit W pour obtenir K, qui a la forme (2, 12) puisqu’il y a 2 noyaux et que chaque noyau a 12 éléments. Voici à quoi ressemble K:

Maintenant nous pouvons multiplier K par P ce qui donne :

Enfin, nous remodelons la K P à la forme correcte, qui selon la formule est une « image » de forme (1, 5). Cela signifie que le résultat de cette convolution est un tenseur de forme (2, 1, 5) puisque nous avons réglé les canaux de sortie sur 2. Voici à quoi ressemble le résultat final:

Ce qui, comme prévu, se vérifie si nous devions effectuer la convolution en utilisant les fonctions intégrées de PyTorch.