Míg az előző fejezet módszerei hasznosak a mintaadatok leírására és megjelenítésére, a statisztika igazi ereje akkor mutatkozik meg, amikor a minták segítségével a populációkról kapunk információt. Ebben az összefüggésben a populáció az érdeklődésre számot tartó objektumok teljes gyűjteménye, például az adatállományunk által képviselt lakáspiac összes egylakásos házának eladási ára. Szeretnénk többet megtudni erről a populációról, hogy segítsen nekünk dönteni arról, hogy melyik lakást vásároljuk meg, de az egyetlen adatunk egy 30 eladási árból álló véletlenszerű minta.

Mindamellett a mintaadatok elemzésével “statisztikai gondolkodást” alkalmazhatunk, hogy következtetéseket vonjunk le az érdeklődő populációra vonatkozóan. Különösen a modell fogalmát használjuk – a valós világ matematikai absztrakcióját -, amelyet a mintaadatokhoz illesztünk. Ha ez a modell ésszerű illeszkedést biztosít az adatokhoz, vagyis ha képes közelíteni az adatok változásának módját, akkor feltételezzük, hogy a modell a populáció viselkedését is képes közelíteni. Ezután a modell szolgáltatja az alapot a populációval kapcsolatos döntések meghozatalához, például a minták azonosítása, az eltérések magyarázata és a jövőbeli értékek előrejelzése révén. Természetesen ez a folyamat csak akkor működhet, ha a minta adatai reprezentatívnak tekinthetők a populációra nézve.

Néha, még ha tudjuk is, hogy a mintát nem véletlenszerűen választották ki, akkor is modellezhetjük azt. Ilyenkor lehet, hogy a mintából nem tudunk formálisan következtetni a populációra, de a minta mögöttes szerkezetét még mindig modellezhetjük. Erre példa lehet egy kényelmi minta – egy olyan minta, amelyet inkább kényelmi okokból választottak ki, mint statisztikai tulajdonságai miatt. Az ilyen minták modellezésekor minden eredményt azzal az óvatossággal kell közölni, hogy a következtetéseket a mintában szereplő objektumokhoz hasonló objektumokra kell korlátozni. Egy másik példa az, amikor a minta a teljes populációból áll. Például modellezhetjük az Amerikai Egyesült Államok mind az 50 államának adatait, hogy jobban megértsük az államok közötti esetleges mintákat vagy szisztematikus összefüggéseket.

Mivel a való világ rendkívül bonyolult lehet (az adatértékek változása vagy egymásra hatása tekintetében), a modellek azért hasznosak, mert egyszerűsítik a problémákat, így jobban megérthetjük azokat (és így hatékonyabb döntéseket hozhatunk). Ezért egyrészt szükségünk van arra, hogy a modellek elég egyszerűek legyenek ahhoz, hogy könnyen használhassuk őket döntések meghozatalához, másrészt viszont olyan modellekre van szükségünk, amelyek elég rugalmasak ahhoz, hogy jó közelítéseket adjanak összetett helyzetekre. Szerencsére az évek során számos olyan statisztikai modellt fejlesztettek ki, amelyek hatékony egyensúlyt biztosítanak e két kritérium között. Az egyik ilyen modell, amely jó kiindulópontot nyújt a későbbiekben vizsgált bonyolultabb modellekhez, a normális eloszlás.

Statisztikai szempontból a valószínűségi eloszlás egy olyan elméleti modell, amely leírja, hogyan változik egy véletlen változó. A mi céljainkra egy véletlen változó a populációban az érdeklődésre számot tartó adatértékeket reprezentálja, például a lakáspiacunkon az összes egylakásos ház eladási árát. Az adatértékek populációs eloszlásának egyik ábrázolási módja az 1.1. szakaszban ismertetett hisztogram. A különbség most az, hogy a hisztogram a teljes sokaságot jeleníti meg, nem pedig csak a mintát. Mivel a populáció sokkal nagyobb, mint a minta, a hisztogram bínjei (az adatok egymást követő tartományai, amelyek a sávok vízszintes intervallumait alkotják) sokkal kisebbek lehetnek, például az alábbiakban egy 1000 eladási árból álló szimulált populáció hisztogramja látható.

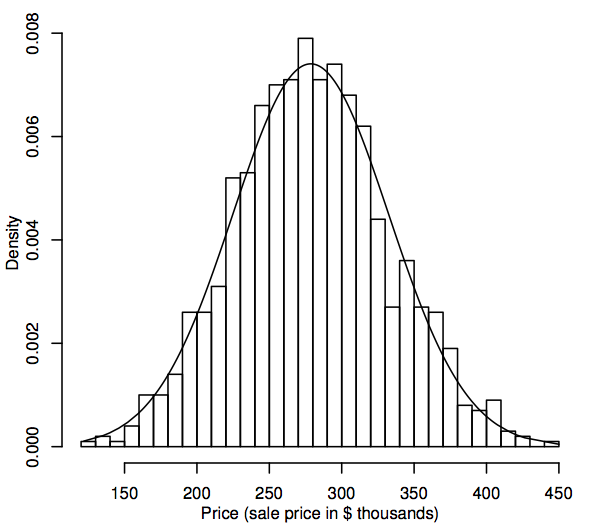
Amint a populáció mérete egyre nagyobb lesz, elképzelhető, hogy a hisztogram sávjai egyre vékonyabbak és számosabbak lesznek, amíg a hisztogram inkább egy sima görbére hasonlít, mint egy lépcsősorra. Ezt a sima görbét sűrűséggörbének nevezzük, és úgy gondolhatunk rá, mint a populációs hisztogram elméleti változatára. A sűrűségi görbék a valószínűségi eloszlások, például a normális eloszlás szemléltetésére is módot adnak. A normál sűrűséggörbe a fenti hisztogramra van ráhelyezve. A szimulált népesség hisztogramja meglehetősen szorosan követi a görbét, ami arra utal, hogy ez a szimulált népességeloszlás meglehetősen közel áll a normálishoz.

Hogy lássuk, hogyan bizonyulhat hasznosnak egy elméleti eloszlás az olyan népességekre vonatkozó statisztikai következtetések levonásához, mint amilyen a lakásár-példánkban szerepel, közelebbről meg kell vizsgálnunk a normális eloszlást. Kezdjük a normáleloszlás egy sajátos változatával, a standard normáleloszlással, amelyet az alábbi sűrűséggörbe ábrázol.

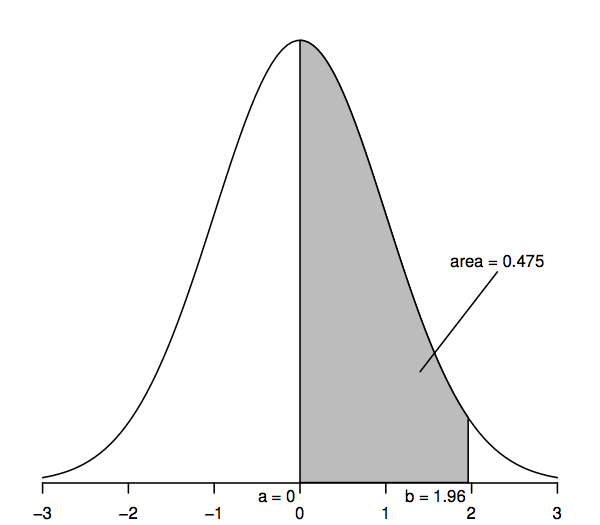
A standard normáleloszlást követő véletlen változók átlaga 0 (tehát a görbe 0 körül szimmetrikus, ami a görbe legmagasabb pontja alatt van) és szórása 1 (tehát a görbének van egy fordulópontja – ahol a görbe először az egyik, majd a másik irányba hajlik – a +1 és -1 pontnál). A normál sűrűséggörbét néha “haranggörbének” is nevezik, mivel alakja hasonlít egy harangéhoz.

A normál sűrűséggörbe legfontosabb jellemzője, amely lehetővé teszi számunkra a statisztikai következtetések levonását, hogy a görbe alatti területek valószínűségeket jelentenek. A görbe alatti teljes terület egy, míg a görbe alatti terület a vízszintes tengely egyik pontja (mondjuk a) és egy másik pont (mondjuk b) között azt a valószínűséget jelenti, hogy egy standard normális eloszlást követő véletlen változó a és b között van. Így például a fenti ábrán látható, hogy a valószínűség 0.475, hogy egy standard normális eloszlású véletlen változó a=0 és b=1,96 között van, mivel az a=0 és b=1,96 közötti görbe alatti terület 0,475.

Ezeknek a területeknek vagy valószínűségeknek az értékeit számos forrásból megkaphatjuk: számtáblázatokból, számológépekből, táblázatkezelő vagy statisztikai szoftverekből, honlapokról stb. Az alábbiakban csak néhány kiválasztott értéket nyomtatunk ki, mivel a későbbi számítások többsége a normális eloszlás egy általánosítását, a “t-eloszlást” használja. Továbbá, az olyan területek helyett, mint amilyen a fenti ábrán árnyékolva van, hasznosabb lesz a “farokterületeket” figyelembe venni (pl, a b ponttól jobbra), ezért a későbbi számtáblázatokkal való konzisztencia érdekében a következő táblázat lehetővé teszi az ilyen farokterületek kiszámítását:

Az 1,96-tól jobbra eső felső farokterület 0,025; ez egyenértékű azzal, hogy a 0 és 1,96 közötti terület 0,475 (mivel a görbe alatti teljes terület 1, a 0-tól jobbra eső terület pedig 0,5). Hasonlóképpen, a kétfarkú terület, amely az 1,96-tól jobbra és a -1,96-tól balra eső területek összege, kétszer 0,025, azaz 0,05.

Hogyan segít mindez abban, hogy statisztikai következtetéseket vonjunk le olyan populációkról, mint amilyen a lakásár-példánkban van? A lényege az, hogy egy normális eloszlási modellt illesztünk a mintaadatainkhoz, majd ezt a modellt használjuk arra, hogy következtetéseket vonjunk le a megfelelő populációra vonatkozóan. Például egy normális eloszlásra vonatkozó valószínűségszámításokat használhatunk (a fenti ábrán látható módon), hogy valószínűségi kijelentéseket tegyünk az adott normális eloszlással modellezett populációra vonatkozóan – ennek pontos módját az 1.3. szakaszban mutatjuk be. Mielőtt azonban ezt megtennénk, megállunk, hogy megvizsgáljuk ennek a következtetési sorrendnek egy olyan aspektusát, amely eldöntheti vagy megtörheti a folyamatot. A modell elég jó közelítést nyújt a mintaértékek mintázatához ahhoz, hogy biztosak lehessünk abban, hogy a modell megfelelően reprezentálja a populáció értékeit? Minél jobb a közelítés, annál megbízhatóbbak lesznek a következtetési kijelentéseink.

Korábban láttuk, hogy a sűrűségi görbét egy nagyon nagy mintamérettel rendelkező hisztogramnak lehet elképzelni. Tehát az egyik módja annak, hogy felmérjük, hogy a populációnk normális eloszlási modellt követ-e, az, hogy a mintaadatainkból hisztogramot készítünk, és vizuálisan megállapítjuk, hogy az “normálisnak tűnik-e”, azaz megközelítőleg szimmetrikus és harang alakú. Ez egy kissé szubjektív döntés, de a tapasztalattal azt kell tapasztalnunk, hogy egyre könnyebb lesz megkülönböztetni az egyértelműen nem normális hisztogramokat azoktól, amelyek ésszerűen normálisak. Például, míg a fenti hisztogram egyértelműen normális sűrűséggörbének tűnik, az 1.1. szakaszban szereplő 30 minta eladási árának hisztogramjának normális jellege kevésbé biztos. Az ésszerű következtetés ebben az esetben az lenne, hogy bár ez a minta hisztogram nem tökéletesen szimmetrikus és harang alakú, elég közel áll ahhoz, hogy a megfelelő (hipotetikus) populációs hisztogram is normális lehet.

A normalitás értékelésének alternatív módja a QQ-diagram (kvantilis-kvantilis-diagram), más néven normál valószínűségi diagram készítése, amint az itt látható a lakásárak adataihoz:

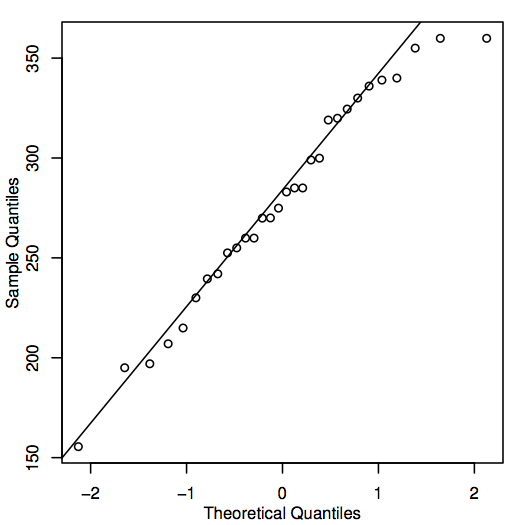
Ha a QQ-diagram pontjai közel fekszenek az átlós vonalhoz, akkor a megfelelő populációs értékek könnyen lehetnek normálisak. Ha a pontok általában messze fekszenek az egyenestől, akkor a normalitás megkérdőjelezhető. Ez ismét egy kissé szubjektív döntés, amelyet a tapasztalattal könnyebb lesz meghozni. Ebben az esetben, tekintettel a meglehetősen kis mintanagyságra, a pontok valószínűleg elég közel vannak az egyeneshez ahhoz, hogy ésszerű a következtetés, hogy a populációs értékek normálisak lehetnek.

A normalitás megítélésére számos kvantitatív módszer is létezik – lásd a 6.3. szakaszt.