Ebben a cikkben elmagyarázom, hogyan valósulnak meg a 2D konvolúciók mátrixszorzatként. A magyarázat a CS231n Convolutional Neural Networks for Visual Recognition (2. modul) című kurzus jegyzetein alapul. Feltételezem, hogy az olvasó ismeri a konvolúciós művelet fogalmát egy mély neurális hálózat kontextusában. Ha nem, akkor ebben a repóban van egy jelentés és kiváló animációk, amelyek elmagyarázzák, hogy mi is az a konvolúció. A cikkben szereplő számításokat reprodukáló kód letölthető innen.
Kis példa
Tegyük fel, hogy van egy egycsatornás 4 x 4 képünk, X, és a pixelértékei a következők:

Tegyük fel továbbá, hogy definiálunk egy 2D konvolúciót a következő tulajdonságokkal:

Ez azt jelenti, hogy 9 db 2 x 2 képfolt lesz, amelyeket elemenként megszorozzuk a W mátrixszal, így:

Ezek a képfoltok 4 dimenziós oszlopvektorokként ábrázolhatók, és egymáshoz kapcsolva egyetlen 4 x 9-es mátrixot, P-t alkotnak, a következőképpen:

Megjegyezzük, hogy a P mátrix i-edik oszlopa valójában az i-edik képfoltot jelenti oszlopvektor formájában.
A konvolúciós réteg súlyainak mátrixa, W, egy 4 dimenziós sorvektorra , K, lapítható a következőképpen:
A konvolúció elvégzéséhez először mátrixszorozzuk meg K-t P-vel, hogy egy 9 dimenziós sorvektort (1 x 9 mátrix) kapjunk, ami azt adja:

Ezután a K P eredményét átformáljuk a megfelelő alakra, ami egy 3 x 3 x 1 mátrix (csatorna dimenzió utolsó). A csatornadimenzió 1, mert a kimeneti szűrőket 1-re állítjuk. A magasság és szélesség 3, mert a CS231n jegyzet szerint:

Ez azt jelenti, hogy a konvolúció eredménye:
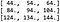
Az ellenőrzés akkor történik meg, ha a PyTorch beépített függvényeivel végezzük el a konvolúciót (a részletekért lásd a cikkhez tartozó kódot).
Nagyobb példa
Az előző pontban szereplő példa egyetlen képet feltételez, és a konvolúció kimeneti csatornái 1-et. Mi változna, ha lazítanánk ezeken a feltételezéseken?
Tegyük fel, hogy a konvolúció bemenete egy 4 x 4-es kép 3 csatornával, a következő pixelértékekkel:

A konvolúciónkat úgy állítjuk be, hogy ugyanazokkal a tulajdonságokkal rendelkezzen, mint az előző részben, kivéve, hogy a kimeneti szűrője 2 legyen. Ez azt jelenti, hogy a kezdeti súlymátrixnak, W-nek, (2, 2, 2, 2, 3) alakúnak kell lennie, azaz (kimeneti szűrők, kernel magasság, kernel szélesség, bemeneti kép csatornái). Állítsuk be, hogy W a következő értékeket kapja:

Megjegyezzük, hogy minden kimeneti szűrőnek saját kernele lesz (ezért van 2 kernelünk ebben a példában), és minden kernel csatornája 3 (mivel a bemeneti képnek 3 csatornája van).
Mivel továbbra is egy 2 x 2 kernelt konvolválunk egy 4 x 4-es képen 0 nulla kitöltéssel és 1 stride-tal, a képfoltok száma továbbra is 9 marad. A képfoltok P mátrixa azonban más lesz. Pontosabban, a P i-edik oszlopa az i. képfoltnak megfelelő 1., 2. és 3. csatornaértékek (mint oszlopvektor) összevonása lesz. A P most egy 12 x 9-es mátrix lesz. A sorok száma 12, mivel minden képfolt 3 csatornával rendelkezik, és minden csatorna 4 elemmel rendelkezik, mivel a kernelméretet 2 x 2-re állítottuk be. Így néz ki a P:

A W-hez hasonlóan minden kernelt sorvektorrá lapítunk, és soronként összefűzzük, hogy 2 x 12-es mátrixot, K-t kapjunk. A K i-edik sora az i-edik kernelnek megfelelő 1., 2. és 3. csatornaértékek (sorvektor formájában) összevonása. Így fog kinézni K:

Már csak a K P mátrixszorzást kell elvégezni és a megfelelő alakra alakítani. A helyes alak egy 3 x 3 x 2 mátrix (a csatornadimenzió az utolsó). Íme a szorzás eredménye:

És íme az eredmény, miután átformáltuk egy 3 x 3 x 2 mátrixra:

Az ismét ellenőrzi, ha a PyTorch beépített függvényeivel végezzük a konvolúciót (a részletekért lásd a cikkhez tartozó kódot).
Szóval mi?
Miért kellene törődnünk azzal, hogy a 2D konvolúciókat mátrixszorzatokkal fejezzük ki? Amellett, hogy van egy hatékony, GPU-n futtatható implementációnk, e megközelítés ismerete lehetővé teszi számunkra, hogy egy mély konvolúciós neurális hálózat viselkedéséről gondolkodjunk. Például a He et. al. (2015) a 2D konvolúciókat mátrixszorzatokkal fejezték ki, ami lehetővé tette számukra, hogy a véletlen mátrixok/vektorok tulajdonságait alkalmazva érveljenek egy jobb súlyok inicializálási rutinja mellett.
Következtetés
Ebben a cikkben két kis példán végigsétálva elmagyaráztam, hogyan lehet 2D konvolúciókat végrehajtani mátrixszorzások segítségével. Remélem, ez elegendő ahhoz, hogy általánosíthassunk tetszőleges bemeneti képméretekre és konvolúciós tulajdonságokra. Szóljon a hozzászólásokban, ha valami nem világos.
1D konvolúció
A cikkben leírt módszer általánosítható 1D konvolúciókra is.
Tegyük fel például, hogy a bemenet egy 3 csatornás 12 dimenziós vektor, így:

Ha az 1D konvolúciónkat a következő paraméterekre állítjuk:
- kernel size: 1 x 4
- output channels: 2
- stride: 2
- padding: 0
- bias: 0
Akkor a konvolúciós művelet paraméterei, W, egy (2 , 3, 1, 4) alakú tenzor lesz. Állítsuk be, hogy W a következő értékeket kapja:

A konvolúciós művelet paraméterei alapján a “kép” foltok P, mátrixa (12, 5) alakú lesz (5 képfolt, ahol minden képfolt egy 12-D vektor, mivel egy folt 4 elemmel rendelkezik 3 csatornán keresztül) és így fog kinézni:

A következő lépésben laposítjuk W-t, hogy megkapjuk K-t, amelynek alakja (2, 12), mivel 2 kernel van, és minden kernel 12 elemű. Így néz ki K:
Most megszorozhatjuk K-t P-vel, ami azt adja:

Végül alakítsuk át a K P-t a megfelelő alakra, ami a képlet szerint egy (1, 5) alakú “kép”. Ez azt jelenti, hogy a konvolúció eredménye egy (2, 1, 5) alakú tenzor, mivel a kimeneti csatornákat 2-re állítottuk. Így néz ki a végeredmény:

Ami a várakozásoknak megfelelően ellenőrizhető, ha a PyTorch beépített függvényeivel végeznénk a konvolúciót.