A Bayes-hiedelemhálózat vagy Bayes-hálózat, vagy hit-hálózat egy valószínűségi grafikus modell (PGM), amely a véletlen változók közötti feltételes függőségeket egy irányított aciklikus gráfon (DAG) keresztül reprezentálja.
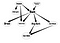
A mai napon megpróbálom ismertetni a Belief Networks főbb aspektusait, különösen olyan alkalmazások esetében, amelyek a Social Network Analysis(SNA)-hoz kapcsolódhatnak. Emellett bemutatok egy példaimplementációt is erre a fajta hálózatra.
Mire használjuk a Bayes-hálózatokat?
A Bayes-hálózatokat számos területen alkalmazzák. Például betegségdiagnosztika, optimalizált webes keresés, spamszűrés, génszabályozó hálózatok stb. És ez a lista még bővíthető. Ezeknek a hálózatoknak a fő célja, hogy megpróbálják megérteni az oksági kapcsolatok szerkezetét. Ennek tisztázása érdekében tekintsünk egy betegségdiagnosztikai problémát. Adott tünetekkel és a belőlük eredő betegséggel felépítjük a Belief Networkünket, és amikor egy új beteg érkezik, az egyes betegségek valószínűségeinek megadásával következtethetünk arra, hogy melyik betegség vagy betegségek lehetnek az új betegnél. Hasonlóképpen más problémákra is felépíthetjük ezeket az ok-okozati összefüggéseket, és következtetési technikákat alkalmazva érdekes eredményekre juthatunk.
Gyors valószínűségi áttekintés
Mielőtt folytatnánk, emlékezetünk felfrissítésére hadd adjam meg a feltételes tulajdonság definícióját. A feltételes valószínűség egy véletlen változó valószínűsége, ha egy másik véletlen változó adott. Megmutatja
Ha ez a két véletlen változó függő,
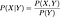
ha független, akkor
Hiedelemhálózatok matematikai definíciója
A valószínűségeket kiszámítjuk. a hiedelemhálózatokban a következő képlettel
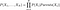
A képletből érthető, ahhoz, hogy ki tudjuk számítani az együttes eloszlást, szükségünk van a hálózat által jelzett feltételes valószínűségekre. De továbbá, hogy ha megvan a közös eloszlás, akkor elkezdhetünk érdekes kérdéseket feltenni. Például az első példában az “ESŐ” valószínűségére kérdezünk rá, ha az “ÉVSZAK” “TÉL” és a “KUTYA BARK” “IGAZ”.
Python példa a Belief Networkre
Szóval, azt hiszem, ennyi elég az elméletből, lássunk néhány valós példát az aktuális kedvenc programozási nyelvemmel, a Pythonnal ❤️ Mielőtt folytatnánk, itt találod az általam írt Jupyter Notebookot.
# create the nodes
season = BbnNode(Variable(0, 'season', ), )
atmos_pres = BbnNode(Variable(1, 'atmos_press', ), )
allergies = BbnNode(Variable(2, 'allergies', ), )
rain = BbnNode(Variable(3, 'rain', ), )
grass = BbnNode(Variable(4, 'grass', ), )
umbrellas = BbnNode(Variable(5, 'umbrellas', ), )
dog_bark = BbnNode(Variable(6, 'dog_bark', ), )
cat_mood = BbnNode(Variable(7, 'cat_mood', ), )
cat_hide = BbnNode(Variable(8, 'cat_hide', ), )bbn = Bbn() \
.add_node(season) \
.add_node(atmos_pres) \
.add_node(allergies) \
.add_node(rain) \
.add_node(grass) \
.add_node(umbrellas) \
.add_node(dog_bark) \
.add_node(cat_mood) \
.add_node(cat_hide) \
.add_edge(Edge(season, allergies, EdgeType.DIRECTED)) \
.add_edge(Edge(season, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(season, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(atmos_pres, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, grass, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, dog_bark, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, cat_mood, EdgeType.DIRECTED)) \
.add_edge(Edge(dog_bark, cat_hide, EdgeType.DIRECTED)) \
.add_edge(Edge(cat_mood, cat_hide, EdgeType.DIRECTED))
Először is leírtuk a csomópontjainkat feltételes valószínűségekkel. Észre kell venned, hogy az egyszerűség kedvéért kihagytam néhány lehetséges állapotértéket. Például az évszak változó más értékeket vesz fel: “tavasz” és “ősz”. Az ötlet tehát ugyanaz.
Nem, ellenőrizzük, hogy a hálózatunk megfelelően van-e felépítve vagy sem.
with warnings.catch_warnings():
warnings.simplefilter('ignore')
graph = convert_for_drawing(bbn)
pos = nx.nx_agraph.graphviz_layout(graph, prog='neato')plt.figure(figsize=(20, 10))
plt.subplot(121)
labels = dict()
nx.draw(graph, pos=pos, with_labels=True, labels=labels)
plt.title('BBN DAG')
Ez a kódrészlet a következő gráfot eredményezné
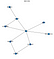
Azt látod, hogy ez a hálózat megfelel az elején készített fantáziarajzomnak. Most pedig végezzünk egy kis következtetést ezen a Belief Networkön.
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()join_tree.set_observation(ev)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
Ez a kódrészlet alapvetően bizonyítékot ad a hálózatnak, amely szerint az évszak a tél 1,0 valószínűséggel. Ennek a bizonyítéknak megfelelően, amikor elvégezzük a következtetést, a következő eredményeket kapjuk.
0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.80000
3=sunny|0.20000
--------------------->
4|grass|grass,no_grass
4=grass|0.70000
4=no_grass|0.30000
--------------------->
1|atmos_press|high,low
1=high|0.50000
1=low|0.50000
--------------------->
5|umbrellas|on,off
5=on|0.95200
5=off|0.04800
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.66000
6=not_bark|0.34000
--------------------->
7|cat_mood|good,bad
7=good|0.23000
7=bad|0.77000
--------------------->
8|cat_hide|hide,show
8=hide|0.87150
8=show|0.12850
--------------------->
Ha további bizonyítékokat adunk hozzá, például a kutya nem ugat
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()ev2 = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('dog_bark')) \
.with_evidence('not_bark', 1.0) \
.build()join_tree.set_observation(ev)
join_tree.set_observation(ev2)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
A következő következtetési eredményeket kapjuk
0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.47059
3=sunny|0.52941
--------------------->
4|grass|grass,no_grass
4=grass|0.53529
4=no_grass|0.46471
--------------------->
1|atmos_press|high,low
1=high|0.39706
1=low|0.60294
--------------------->
5|umbrellas|on,off
5=on|0.88941
5=off|0.11059
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.00000
6=not_bark|1.00000
--------------------->
7|cat_mood|good,bad
7=good|0.52647
7=bad|0.47353
--------------------->
8|cat_hide|hide,show
8=hide|0.83162
8=show|0.16838
--------------------->
Látod a különbséget? 😆 Sok valószínűségi érték megváltozott, amikor hozzáadtuk az ugatással kapcsolatos bizonyítékot. Ez határozottan egy buta példa, de jó megérteni.
Hogyan használjuk a Bayes-hálózatokat az SNA-ban?
A Bayes-hálózatok nagyon hatékony eszközök a változók közötti oksági kapcsolatok szerkezetének megértéséhez. Ha egyszer megtervezte a modellt, még egy kis adathalmaz esetén is számos dolgot meg tud mondani. A kérdés ebben a részben az, hogyan lehet kihasználni a Bayes-hálók előnyeit az SNA-ban. A válasz nem egyedi, de kezdjük egy mélyreható gondolattal. Az SNA-ban megpróbáljuk megérteni egy társadalmi hálózat szerkezetét. Ezenkívül megpróbáljuk megérteni a csomópontok fontosságát. De nem tudjuk, hogy a fontossági metrikáinknak milyen eredményei vannak. Ez az a pont, ahol a Bayes-hálózatok zajlanak. Ha például úgy gondoljuk, hogy egy csomópont fontosságát a Degree Centrality és a Link Centrality okozza, akkor a következő hálózatot kaphatjuk:
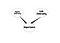
Ez egy nagyon naiv Bayes-hálózat. A csomópontok fontosságának meghatározása mellett további alkalmazás lehet a csomópontok valamilyen speciális típusának keresése. Vegyünk egy olyan Szociális Hálózatot, amelyben vannak olyan emberek, akik potenciális vezetők, és őket szeretném megkeresni. Tekintsük a következő gráfot
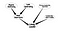
Ez a kicsit bonyolultabb hálózat segít meghatározni a vezetői szereppel kapcsolatos csomópontok bizonytalanságát.
Egy másik alkalmazás a kapcsolatok kikövetkeztetése lenne. Az új kapcsolatokat a meglévőkből lehet kikövetkeztetni. Például egy közösségi hálózatban a csoporttagságból valószínűsíthető tagsági kapcsolatra lehet következtetni. Úgy értettem, hogy a meglévő kapcsolatok figyelembevételével modellezhetünk új kapcsolatot a felhasználók és a csoportok között. Lásd a következő modelldiagramot
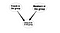
Szóval, ezek néhány alapvető példa arra, hogyan alkalmazhatók a Bayes-hálózatok az SNA-ban. Ezt a témát nem nagyon tanulmányozták, de úgy gondolom, hogy nagyon hasznos lehet a további tanulmányozása.
Következtetés
A Bayes-hálózatokkal kapcsolatban a nehéz dolog a tervezés. Különösen, ha az SNA-ra gondolsz, a Szociális Hálózat leképezésének megkonstruálása a Bayes-hálózattal inkább művészet, mint tudomány 😃 De ha egyszer elvégezted a művészi munkát és nagyon jól megtervezted a modellt, ezek a praktikus eszközök sok mindent elmondhatnak. Mint tudjuk, a Bayes-hálózatokat rengetegféle területen alkalmazzák. A legtöbb esetben nagyon jól működött. Ezért erősen hiszem, hogy a szociális hálózatokra is nagyon mélyreható következtetéseket tudunk levonni.
Az SNA és a Bayes-hálózatokkal kapcsolatos további vizsgálatokhoz kérem, maradjon velünk 🚀
.