Definíció
Egy polinom az x változóban olyan függvény, amely az alábbi formában írható fel,
ahol an, an-1 , …, a2, a1, a0 konstansok. Az x legnagyobb hatványát tartalmazó kifejezést (azaz anxn) nevezzük vezető kifejezésnek, an-t pedig vezető együtthatónak. A polinom foka az x-nek a vezető tagban lévő hatványa. Láttunk már 0, 1 és 2 fokú polinomokat, amelyek az állandó, a lineáris és a kvadratikus függvények voltak. A 3., 4. és 5. fokú polinomoknak speciális nevük is van: köbös, kvartikus és kvintikus függvények. Az n > 5 fokú polinomokat egyszerűen n-edik fokú polinomoknak nevezik. A különböző polinomfüggvények neveit az alábbi táblázat foglalja össze.
| A polinom fokozata | A függvény neve |
| 0 | Konstans függvény. |
| 1 | Lineáris függvény |
| 2 | négyzetes függvény |
| 3 | Kubikus függvény |
| 4 | Kvartikus függvény |
| 5 | Kvintikus függvény |
| n (ahol n > 5) | n-edik fokú polinom |
A polinomok néhány példája:
A polinomok korlátozó viselkedése
A függvény korlátozó viselkedése leírja, hogy mi történik a függvénnyel, ha x → ±∞. Egy polinom fokozata és a vezető együtthatójának előjele határozza meg a határviselkedését. Különösen
Ezeket az eredményeket az alábbi táblázat foglalja össze.
Ezek az információk segítségével egyszerűen a gráfját megvizsgálva megállapíthatjuk, hogy egy polinom páratlan vagy páros fokú-e, és hogy a vezető együtthatója pozitív vagy negatív.
A következő polinomok grafikonjai a fenti táblázatban vázolt viselkedések mindegyikét példázzák.
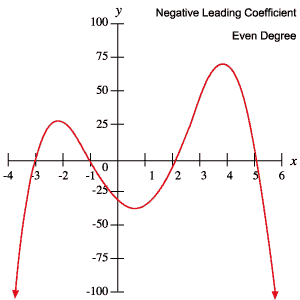
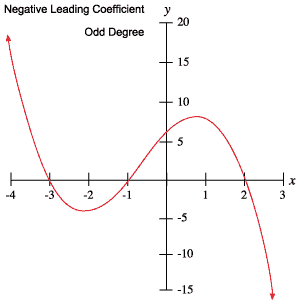
Gyökerek és fordulópontok
A polinom fokszáma még többet elárul róla, mint a határérték viselkedése. Konkrétan, egy n-edik fokú polinomnak a szorzatokat számolva legfeljebb n valós gyöke (x-pontja vagy nullája) lehet. Tegyük fel például, hogy egy 6. fokú polinomot vizsgálunk, amelynek 4 különböző gyöke van. Ha a négy gyök közül kettőnek a szorossága 2, a másik kettőnek pedig 1, akkor tudjuk, hogy nincs más gyök, mert mind a 6 gyökkel számoltunk. Ez azért van így, mert a kettes szorosságú gyökök (más néven kettős gyökök) két gyöknek számítanak.
Tudjuk, hogy egy n-edik fokú polinomnak nem kell, hogy n valós gyöke legyen – lehet kevesebb is, mert vannak képzeletbeli gyökei. Vegyük észre, hogy egy páratlan fokú polinomnak legalább egy valós gyökkel kell rendelkeznie, mivel a függvény egyik végén – ∞-hez, a másik végén + ∞-hez közelít; egy folytonos függvénynek, amely negatívról pozitívra vált, valahol a kettő között kell metszeni az x-tengelyt. Ezenkívül egy n-edik fokú polinomnak legfeljebb n – 1 fordulópontja lehet. A fordulópont az a pont, ahol a függvény növekvőből csökkenőre vagy csökkenőből növekvőre vált, ahogy az alábbi ábrán látható. Ismétlem, egy n-edik fokú polinomnak nem kell, hogy n-1 fordulópontja legyen, lehet kevesebb is.
Vigyázat
Fontos, hogy felismerjük a különbséget a páros és páratlan függvények, illetve a páros és páratlan fokú polinomok között. Bármely függvény, f(x), vagy páros, ha,
f(-x) = x,
az f(x) tartományában lévő minden x-re, vagy páratlan, ha,
f(-x) = -x,
az f(x) tartományában lévő minden x-re, vagy sem páros, sem páratlan, ha a fenti állítások egyike sem igaz.
Egy p(x) k-edik fokú polinomról azt mondjuk, hogy páros fokú, ha k páros szám, és páratlan fokú, ha k páratlan szám. Ne feledjük, hogy még ha p(x) páros fokú is, nem feltétlenül páros függvény. Hasonlóképpen, ha p(x) páratlan fokú, akkor sem feltétlenül páratlan függvény.
A páros és páratlan kifejezéseket használjuk a polinomok gyökeinek leírására is. Konkrétan, egy p(x) polinomnak x = a gyöke k sokszorosságú (azaz x = a egy k-szor ismételt gyök), ha (x – a)k a p(x) egyik tényezője. Azt mondjuk, hogy x = a páros szorosságú, ha k páros szám, és páratlan szorosságú, ha k páratlan szám.
Tartomány és tartomány
Minden polinomnak ugyanaz a tartománya, amely az összes valós számból áll. A páratlan fokú polinomok tartománya szintén az összes valós számból áll. A páros fokú polinomok tartománya egy kicsit bonyolultabb, és nem tudjuk egyértelműen megadni az összes páros fokú polinom tartományát. Ha a vezető együttható pozitív, a függvény + ∞-ig terjed, míg ha a vezető együttható negatív, akkor – ∞-ig terjed. Ez azt jelenti, hogy a pozitív vezető együtthatójú páros fokú polinomok tartománya olyan, ahol ymax a függvény által elért globális maximumot jelöli. Általában nem lehet analitikusan meghatározni a polinomok maximumát vagy minimumát.
*****
A következő részben a polinomosztást, a polinomfüggvények gyökeinek megtalálására használt technikát ismerhetjük meg.
Polinomosztás