A klasszifikáció egy felügyelt gépi tanulási megközelítés, amelyben az algoritmus tanul a neki megadott bemeneti adatokból – majd ezt a tanulást használja fel az új megfigyelések osztályozására.
Más szóval, a képzési adathalmazt arra használják, hogy jobb peremfeltételeket kapjanak, amelyek segítségével meghatározhatók az egyes célosztályok; miután ezek a peremfeltételek meghatározásra kerültek, a következő feladat a célosztály előrejelzése.
A bináris osztályozók csak két osztállyal vagy lehetséges kimenettel dolgoznak (példa: pozitív vagy negatív hangulat; a hitelező fizet-e kölcsönt vagy sem; stb.), a többosztályos osztályozók pedig több osztállyal dolgoznak (példa: melyik országhoz tartozik egy zászló, egy kép alma, banán vagy narancs; stb.). A többosztályos osztályozó feltételezi, hogy minden minta egy és csak egy címkét kap.

A gépi tanulásban az egyik első népszerű osztályozó algoritmus a Naive Bayes volt, egy valószínűségi osztályozó, amelyet a Bayes-tétel ihletett (amely lehetővé teszi, hogy a valós világban bekövetkező eseményekre ésszerű következtetéseket vonjunk le az erre utaló megfigyelések előzetes ismerete alapján). A név (“Naiv”) abból ered, hogy az algoritmus feltételezi, hogy az attribútumok feltételesen függetlenek.
Az algoritmus egyszerűen megvalósítható, és általában ésszerű módszert jelent az osztályozási erőfeszítések beindítására. Könnyen skálázható nagyobb adathalmazokra (lineáris időt vesz igénybe, szemben az iteratív közelítéssel, amelyet sok más típusú osztályozó esetében használnak, ami a számítási erőforrások szempontjából drágább), és kis mennyiségű képzési adatot igényel.
A Naive Bayes azonban szenvedhet a “nulla valószínűség problémája” néven ismert problémától, amikor a feltételes valószínűség nulla egy adott attribútumra, és nem ad érvényes előrejelzést. Az egyik megoldás egy simító eljárás (pl. Laplace-módszer) kihasználása.

P(c|x) az osztály (c, cél) utólagos valószínűsége adott prediktor (x, attribútumok) esetén. P(c) az osztály előzetes valószínűsége. P(x|c) a valószínűség, amely a prediktor adott osztályra vonatkozó valószínűsége, és P(x) a prediktor előzetes valószínűsége.
Az algoritmus első lépése az előzetes valószínűség kiszámításáról szól adott osztálycímkékre. Ezután a valószínűségi valószínűség megtalálása minden egyes attribútummal, minden egyes osztályra. Ezt követően ezeket az értékeket Bayes-formulába & helyezve kiszámítjuk az utólagos valószínűséget, majd megnézzük, hogy melyik osztály valószínűsége a nagyobb, ha a bemenet a nagyobb valószínűségű osztályba tartozik.
A Naive Bayes-t meglehetősen egyszerűen implementálhatjuk Pythonban a scikit-learn könyvtár felhasználásával. A scikit-learn könyvtár alatt valójában háromféle Naive Bayes modell létezik: (a) Gauss-típus (feltételezi, hogy a jellemzők harangszerű, normális eloszlást követnek), (b) Multinomiális (diszkrét számlálásokhoz használatos, az x kísérletekben megfigyelt kimenetel mennyiségét tekintve), és (c] Bernoulli (hasznos bináris jellemzővektorokhoz; népszerű felhasználási eset a szövegosztályozás).
Egy másik népszerű mechanizmus a döntési fa. Adott egy attribútumokból álló adat az osztályokkal együtt, a fa olyan szabályok sorozatát állítja elő, amelyek felhasználhatók az adatok osztályozására. Az algoritmus a mintát két vagy több homogén halmazra (levélre) osztja fel a bemeneti változók legjelentősebb megkülönböztető elemei alapján. A differenciáló tényező (prediktor) kiválasztásához az algoritmus figyelembe veszi az összes jellemzőt, és bináris felosztást végez rajtuk (kategorikus adatok esetén a felosztás macska szerint; folytonos adatok esetén válasszon egy határértéket). Ezután kiválasztja azt, amelyik a legkisebb költséggel jár (azaz a legnagyobb pontosságú), és ezt rekurzívan addig ismétli, amíg sikeresen fel nem osztja az adatokat az összes levélben (vagy el nem éri a maximális mélységet).
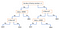
A döntési fák általában egyszerűen érthetők és vizualizálhatók, kevés adatelőkészítést igényelnek. Ez a módszer numerikus és kategorikus adatokat is képes kezelni. Másrészt az összetett fák nem általánosítanak jól (“túlillesztés”), és a döntési fák némileg instabilak lehetnek, mivel az adatok kis eltérései egy teljesen más fa generálását eredményezhetik.
A döntési fákból származó osztályozási módszer a Random Forest, amely lényegében egy “meta-becslő”, amely számos döntési fát illeszt az adathalmazok különböző almintáira, és az átlagot használja a modell előrejelzési pontosságának javítására és a túlillesztés megfékezésére. A részminták mérete megegyezik az eredeti bemeneti minta méretével – de a mintákat helyettesítéssel húzza ki.
A Random Forest általában nagyobb fokú robusztusságot mutat a túlillesztéssel szemben (>robusztusság az adatok zajával szemben), hatékony végrehajtási idővel még nagyobb adathalmazok esetén is. Kiegyensúlyozatlan adathalmazok esetén azonban érzékenyebbek, ugyanakkor kissé bonyolultabb az értelmezésük, és több számítási erőforrást igényelnek.
Egy másik népszerű osztályozó az ML-ben a logisztikus regresszió – ahol az egyes kísérletek lehetséges kimeneteleit leíró valószínűségeket egy logisztikus függvény segítségével modellezik (a név ellenére osztályozási módszer):

Íme, így néz ki a logisztikus egyenlet:
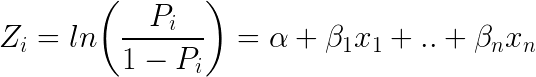
Az egyenlet mindkét oldalára e-t (exponens) véve az egyenlet mindkét oldalán az alábbi eredményt kapjuk:
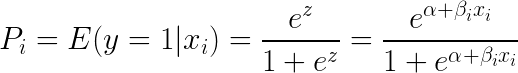
A logisztikus regresszió leginkább több független változó egyetlen kimeneti változóra gyakorolt hatásának megértésére alkalmas. A bináris osztályozásra összpontosít (több osztályt tartalmazó problémákra a logisztikus regresszió olyan kiterjesztéseit használjuk, mint a multinomiális és az ordinális logisztikus regresszió). A logisztikus regresszió népszerű az olyan felhasználási esetekben, mint a hitelelemzés és a válaszadási/vásárlási hajlandóság.
Végül, de nem utolsósorban a kNN (a “k legközelebbi szomszédok”) szintén gyakran használatos osztályozási problémákhoz. A kNN egy egyszerű algoritmus, amely az összes elérhető esetet tárolja, és az új eseteket egy hasonlósági mérték (pl. távolságfüggvények) alapján osztályozza. A statisztikai becslésben és mintafelismerésben már az 1970-es évek elején használták nem-parametrikus technikaként:

