(IUCr) Szimmetriaelemek szimbólumai

Acta Cryst. (1992). A48, 727-732

A Nemzetközi Kristallográfiai Unió Ad-Hoc Bizottságának végleges jelentése a szimmetria nómenklatúrájáról*

By P. M. DE WOLFF (elnök), Meermanstraat 126, 2614 AM Delft, Hollandia,

Y. BILLIET, Ecole Nationale d’Ingénieurs, BPW 3038 Sfax, Tunézia,

J. D. H. DONNAY, Geológiai Tudományok Tanszék, McGill Egyetem, 3450 University Street, Montreal, Kanada H3A 2A7,

W. FISCHER, Institut für Mineralogie, Petrologie und Kristallographie der Phillips-Universität, Lahnberge, D-3550 Marburg (Lahn), Németország,

R. B. GALIULIN, Institute of Crystallography, Academy of Sciences of Russia, Leninsky Prospekt 59, Moscow 117333, Russia,

A. M. GLAZER, Clarendon Laboratory, University of Oxford, Parks Road, Oxford OX1 3PU Anglia,

TH. HAHN, Institut für Kristallographie, RWTH, Templergraben 55, D-5100 Aachen, Németország,

MARJORIE SENECHAL, Department of Mathematics, Smith College, Northampton, MA 01063, USA,

D. P. SHOEMAKER, Kémia Tanszék, Oregoni Állami Egyetem, OR 97331, USA,

H. WONDRATSCHEK, Institut für Kristallographie, Universität Karlsruhe, Kaiserstrasse 12, D-7500 Karlsruhe 1, Németország,

A. J. C. WILSON (ex officio, IUCr Commission on International Tables), Crystallographic Data Centre, University Chemistry Laboratory, Lensfield Road, Cambridge CB2 1EW, England

AND S. C. C. ABRAHAMS (ex officio, IUCr Commission on Crystallographic Nomenclature), Department of Physics, Southern Oregon State College, 1250 Siskiyou Boulevard, Ashland, OR 97520-5047, USA

(1991. november 7-én érkezett; elfogadva 1992. március 9-én)

* Kinevezve 1984. november 14-én, módosítva 1987. augusztus 10-én az Acta Cryst. (1979), A35, 1072. Az IUCr Kristallográfiai Nómenklatúra Bizottsága által 1991. december 23-án, a Végrehajtó Bizottság által 1992. március 9-én elfogadott zárójelentés.

Abstract

A szimmetriaelemek nemrég elfogadott újradefiniálásának fényében új vagy újradefiniált nyomtatott jeleket javasolnak . Az e betű különösen bizonyos olyan siklósíkokat takar, amelyeknek eddig nem volt egyedi szimbóluma, mint például az “a vagy b” elnevezésűek. Az e betű használata öt különböző tércsoport Hermann-Mauguin szimbólumában javasolt. A síkkal párhuzamos irányban vetített e síkok számára egy olyan grafikus szimbólumot javasolunk, amely megszünteti a jelenlegi elnevezésükből adódó kétértelműséget. A k betűt javasoljuk a siklósíkok egy újonnan meghatározott osztályára, amelyeknek eddig nem volt külön szimbólumuk. Az International Tables for Crystallography (1989), Vol. A (Dordrecht: Kluwer Academic Publishers) tércsoport-leírásokban bevezetett szimmetriaműveletek szimbólumait javasoljuk általános használatra, csak a siklótükrözési műveletekre vonatkozó módosításokkal.

Bevezetés

A “tércsoportok szimmetriaműveleteivel és szimmetriaelemeivel kapcsolatos nómenklatúraproblémák” vizsgálatára 1980-ban kijelölt Ad-hoc bizottság két jelentést adott ki Nomenclature for Crystal Families, Bravais-Lattice Types and Arithmetic Classes címmel (de Wolff et al., 1985) és a Szimmetriaelemek meghatározása tércsoportokban és pontcsoportokban (de Wolff et al., 1989). Amint az 1989-es jelentésben is szerepel, a szimmetriaműveletekkel kapcsolatban az egyetlen megoldatlan probléma a megfelelő szimbólumok kiválasztása, mivel a fogalom egyértelmű. Az International Tables for Crystallography (1983, 1989) ideiglenes jelölést fogadott el, a továbbiakban ITA83.

A szimmetriaelemek nyomtatott szimbólumai

A szimmetriaelemeknek az 1989-es jelentésben (de Wolff et al.) megadott definícióját használjuk a jelen jelentésben. Itt megismételjük a lényeget:

Minden adott szimmetria művelethez annak geometriai elemét (sík, pont és/vagy vonal) definiáljuk. A szimmetriaelem egy adott tércsoport egyik szimmetriaműveletének geometriai elemének és az adott tércsoport összes olyan szimmetriaműveletének halmazának (az úgynevezett `elemhalmaznak’) a kombinációja, amely osztozik ezen geometriai elemen.

A geometriai elemek explicit definícióit és az ebből következő szimmetriaelemek leírását, valamint szimbólumaikat az 1. és 2. táblázat tartalmazza. (Ezek a síkok kivételével megegyeznek az 1989-es Jelentés 1. és 2. táblázatával, és a teljesség kedvéért itt megismételjük, lásd alább). Minden szimmetriaelemet két karakterből álló szimbólummal ábrázolunk. Az első karakter egy nagybetűs E minden szimmetriaelem esetében. Ez azt jelzi, hogy a szimbólum egy szimmetriaelemre utal, és nem például egy szimmetriaműveletre. Ha ez már a szövegkörnyezetből is egyértelmű, akkor az E-t el lehet hagyni, pl. “egy tengely 2” helyett “egy tengely E2”.

1. táblázat. Szimmetriaműveletek geometriai elemei pont- és tércsoportokban
Szimmetriaművelet	Geometriai elem	Kiegészítő paraméterek
Identitás	Nem kötelező	Nincs
Transzláció	Nem kötelező	Vektor $\mathbf{t}$
Tükrözés az A síkban	A síkban	Nincs
Dia tükrözés =Tükrözés az A síkban és transzláció. $\mathbf{v}$ párhuzamos az A-val	A sík	Gördülő vektor $\mathbf{v}$
forgás a b egyenes körül	b egyenes	A forgás szöge és értelme
csavarforgatás = forgás a b egyenes körül és transzláció $\mathbf{u}$ a b-vel párhuzamosan	B line b	A forgatási csavar vektor $\\mathbf{u}$
Rotoinverzió = forgatás a b egyenes körül és inverzió a b	vonalon lévő P ponton keresztül	vonal b és a b-n lévő P pont	A szög (nem egyenlő $\pi$ ) és a forgás értelme
Inverzió a P ponton keresztül	P pont	Nincs

Az 1989-es jelentésben felsorolt Eg szimbólumot lehet használni a siklósíkokra, ha csupán azt akarjuk megmutatni, hogy a szimmetriaelem egy siklósík. Ha viszont azon speciális fajták valamelyikéhez tartozik, amelyeket már régóta egy megfelelő betűvel jelölnek (a, b, c, n vagy d; vö. ITA83), akkor ez a betű helyettesíti a g-t az Eg-ben.

2. táblázat. Szimmetriaelemek pont- és tércsoportokban
Szimmetriaelem neve	Szimbólum	Geometriai elem	Defináló művelet (d.o.)	Operációk az elemkészletben
Tükörsík	Em	A sík	Tükrözés A-ban	D.o. és annak koplanáris megfelelői*
Dia sík	Eg $\ddag$	A sík	Dia tükrözés A-ban, 2v (nem v) egy rácsáthelyezés	D.o. és koplanáris megfelelői*
Pörgetési tengely	En	B vonal b	Pörgetés b körül, szög $2\pi/n$ ,n = 2, 3, 4 vagy 6	1., $\dots$ ,(n – 1)-edik d.o. hatványa. és koaxiális megfelelőik $\dag$
csavartengely	Enj	vonal b	csavar forgása b körül, szög $2\pi/n$ , u =j/n-szer legrövidebb rács átfordítás b mentén, jobb oldali csavar; n = 2, 3, 4 vagy 6, $j=1,\dots,(n-1)$	1st, $\dots$ ,(n – 1)th d hatványai.o. és koaxiális megfelelőik $\dag$
Rotoinverziós tengely	$E\bar n$	b egyenes és a b-n lévő P pont	Rotoinverzió: forgatás b körül, szög $2\pi/n$ , és inverzió P-n keresztül; n = 3, 4 vagy 6	D.o. és annak inverze
Középpont	$E\bar 1$	P pont	Inverzió P-n keresztül	D.o. csak

* Vagyis az összes siklótükrözés azonos tükrözési síkkal, amelyek siklóvektorai a d.o. vektorától (tükrözés esetén nullának tekintve) egy rácsos transzlációs vektorral különböznek.
$\dag$ Vagyis minden forgatás és csavarforgatás azonos b tengellyel, azonos forgatási szöggel és értelemmel, valamint azonos $\mathbf{u}$ (forgatás esetén nulla) csavarvektorral egy rácsos transzlációs vektorig.
$\ddag$ Eg-ben g helyett a, b, c, n, d, e vagy k szerepel bizonyos típusú siklósíkok esetén, vö. 2. §.

Az Eb-hez hasonló szimbólumoknál azonban egy fontos új szempontra lehet rámutatni. Az ITA83 szerint egy sík b-vel való jelölése csupán azt jelentette, hogy a síkban a b tengely mentén b/2 csúszókomponensű siklótükrözés szimmetriaművelet. Ez a definíció minden bizonnyal érvényes az 1. ábrán ábrázolt helyzetre.

1. ábra. (W. Fischer nyomán.) Egy Eb-csúszósík elemhalmaza, a sík feletti (+) és alatti (-) pontok halmazaként ábrázolva, amelyeket a síkbeli csúszótükröződések hoznak létre, például a bal felső + jelből kiindulva. A síkkal párhuzamos transzlációk (+ $\cdots$ + vektorok) N hálóval jelzett hálója, amely ebben az esetben történetesen téglalap alakú. Mindkét élpár párhuzamos a kristálytengelyekkel. Van egy siklótükör, amelynek siklóvektora (+ $\cdots$ -) a b tengely mentén helyezkedik el.

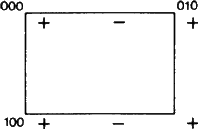
$\begin{figure} \includegraphics {fig1.ps} \end{figure}$

Az 1. ábra, valamint a 2. és 3. ábra a W. Fischer ad hoc bizottsági tag által az összes siklósík-típus leltáraként tervezett hasonló ábrákból származik. Bár a készletet 1980-ban mutatták be a bizottságnak, jóval az 1989-es jelentés megjelenése előtt, az ábrák mindegyike pontosan a siklórepülő “elemkészletét” mutatja a jelentésben meghatározottak szerint (vö. a fenti összefoglalóval). Egy siklósík esetében az elemkészlet minden olyan siklótükörből áll, amelynek közös geometriai eleme a sík. Hatásukat a síkba vetítve mutatjuk be. Bármely + jel kiindulási helyzetéből kiindulva minden – jel a halmaz egyik siklótükröződésének eredménye. Mindezeket a + és – jelek eredő kétdimenziós periodikus mintázatának elemi hálóján belül mutatjuk be.

Gyakran fogunk hivatkozni a síkkal párhuzamos összes transzláció által alkotott N hálóra; ez a háló könnyen szemléltethető, ha csak a + jeleket nézzük. Ezeket a vektorokat élesen meg kell különböztetni a + jelet bármely – jellel összekötő vektoroktól, amelyek mindegyike egy-egy, az elemhalmazba tartozó csúszó tükörkép csúszóvektora.

Az új szempont azért merül fel, mert az ITA83 definíciója szerint a b-sík bizonyos esetekben egyben a-sík is; lásd a 2. ábrát. Ez nyilvánvalóan csak akkor következik be, ha az N háló ortogonálisan centrált, mert akkor az a-csúszás b-csúszássá változtatható (és fordítva) egy centrálási transzláció hozzáadásával. Az eddigi gyakorlat az volt, hogy az ilyen siklósíkot tetszőlegesen a-nak vagy b-nek nevezték, ami indokolatlan torzítást és e szimbólumok egyediségének hiányát okozta. Ezért javasoljuk, hogy a 2. ábra esetét külön szimbólummal fedjük le.

2. ábra. (W. Fischer nyomán.) Egy Ee-csúszó sík elemhalmaza. Vö. az 1. ábra feliratával. Vegyük észre, hogy az N háló itt ortogonálisan centrált.

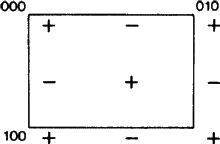
$\begin{figure} \includegraphics {fig2.ps} \end{figure}$

Ezután ennek a szimbólumnak a hatókörét ki kell terjeszteni az átlós irányú, azaz csak egy kristálytengellyel párhuzamos siklósíkokra, feltéve, hogy a siklósíknak e tengely mentén van siklóvektora, és az N háló ortogonális centrális. Az ilyen síkok esetében nincs meg a fenti a-b véletlenszerű választás kétértelműsége, de az új szimbólum kiterjesztett alkalmazási köre összhangban van az összes meglévő szimbóluméval (nevezetesen a, b, c, n és d). Ezek mindegyike olyan siklósíkhoz használható, amelynek egy és két kristálytengelye is van az N hálóban, vö. 3. ábra.

Az e betűt javasoljuk az új szimbólumnak. Így az Ee olyan siklósíkokra fog vonatkozni, amelyekben az N hálók ortogonális központúak, és legalább egy kristálytengely mentén legalább egy siklóvektor van. Ezért új kritériumra van szükség: nevezetesen a siklóvektoroknak a kristály hagyományos tengelyeihez viszonyított orientációjára. Mivel ez utóbbiak szimmetriairányok mentén vannak, míg minden siklósík párhuzamos a rács egy tükörsíkjával, nem meglepő, hogy mindig van legalább egy hagyományos kristálytengely az N-ben. Ha csak egy ilyen tengely van, akkor arra merőlegesen mindig van egy másik transzláció az N-ben.

Az új e szimbólumot, valamint a régi a, b, c, d, n szimbólumokat most újra definiáljuk ezen új kritérium és az N háló Bravais-típusa szerint. Ez a háló monoklin vagy ortogonális vagy tetragonális primitív (mp vagy op vagy tp) vagy ortogonális centrális (oc). Csak az oc típusú N hálók engedik meg az Ee-csúszósíkot. Az En szimbólum az mp vagy op típusú Bravais N hálókra alkalmazható, míg az Ed az oc típusú N hálókra. (Ahogy az ITA83 1.3. táblázatához fűzött lábjegyzetben olvasható: “A d siklósíkok csak az orthorombikus F tércsoportokban, a tetragonális I tércsoportokban, valamint a köbös I és F tércsoportokban fordulnak elő. Mindig párban fordulnak elő, váltakozó siklóvektorokkal”). Az Ea, Eb, Ec és Ee síkokkal ellentétben azonban az En és Ed síkok esetében nincs az N-ben egy hagyományos tengellyel sem párhuzamos, sem arra merőleges siklóvektor.

A fenti típusú siklósíkok ebből következő definícióit a 3. táblázat (i) és (ii) sorai foglalják össze, illetve részletesebben a 3. ábra.

3. táblázat. A siklósíkok speciális fajtáinak nyomtatott szimbólumai
A kristálytengelyekkel párhuzamos vagy merőleges siklóvektorok száma az N hálóban	Bravais típusú háló N
A szimbólumot két kritérium alapján határozzuk meg. Az egyik kritérium a vizsgált síkkal párhuzamos szimmetriatranszlációk által alkotott N háló Bravais típusa (mp, op, tp vagy oc). Ez a háló mindig tartalmaz legalább egy hagyományos kristálytengelyt.* A másik kritérium a siklóvektorok ilyen tengelyekhez viszonyított orientációjára vonatkozik.
	m, op, tp	oc
i) Egy vagy két párhuzamos	Ec(Ea, Eb)	Ee
(ii) Egyik sem párhuzamos, egyik sem merőleges	En	Ed
(iii) Egyik sem párhuzamos, egy merőleges	Ek	–

* Az ITA83, 9. § meghatározása szerint.1; azonban a romboéderes tércsoportok esetében itt csak a hatszögtengelyeket használjuk.

A többi siklósík korábban nem rendelkezett külön szimbólummal. Mindegyik átlós orientációjú (csak egy hagyományos kristálytengely a nettó N-ben). Az elemkészletükben lévő siklótükrök között nincs olyan, amelynek siklóvektora e tengely mentén lenne. Az egyik siklási vektor azonban (szimmetria szerint) merőleges rá. Kívánatosnak tűnik egy szimbólum, ezért ismét egy új betűt javasolunk: k. Az új Ek szimbólumot röviden a 3. táblázat (iii) sorában definiáljuk, és teljes egészében a 3. ábra alsó blokkjában ábrázoljuk. Néhány példát a 2. §-ban találunk.

3. ábra. (W. Fisher rajzaiból átvéve.) A siklósíkok elemkészleteinek összes lehetséges szempontja az 1. ábrához hasonlóan ábrázolva, de a tengelycímkéktől függetlenül. Az ábrák az N hálók Bravais-háló típusú szimbóluma (felső sor) által vezetett oszlopokba vannak csoportosítva, vö. 3. táblázat. Az említett táblázat egyéb kritériumait először a kristálytengelyek síkbeli irányait mutató kettős vonalakkal ellenőrizhetjük. Az N mutatott háló egyik (függőleges) élét mindig egy ilyen tengely mentén választjuk ki. A másik él vízszintes, kivéve az (1) és (8) eseteket. Az (1), $\dots$ ,(5) ábrák esetében a siklósík szimbóluma a függőleges tengely a, b vagy c jelölése; a többinél a diagramot tartalmazó vázlatos blokk bekeretezett betűje. Figyeljük meg a függőleges siklóvektorokat az (1), $\dots$ ,(7) ábrákon, a vízszinteseket a (6), (7), (14), (15) ábrákon, és ezek hiányát a (8), $\dots$ ,(13) ábrákon. Az egyes ábrák alatt egy-egy példa előfordulására a tércsoport szimbólum és a sík koordinátatriplettje található.

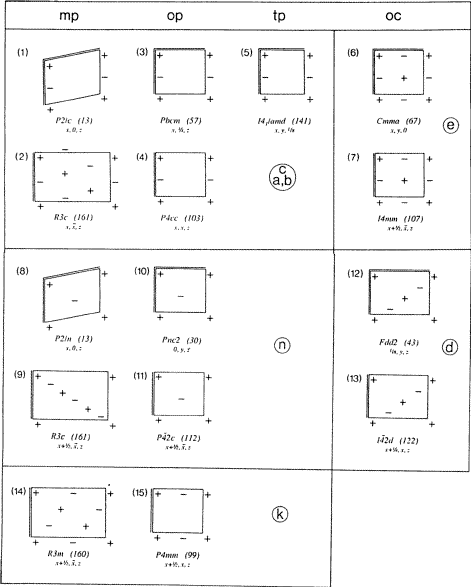
$\begin{figure} \includegraphics {fig3.ps} \end{figure}$

A 3. ábrán az összes siklósík-típus Fischer-féle leltárát mutatjuk be rövidített – bár még mindig teljes – formában, amelyben a kristálytengelyek nagyobb grafikai hangsúlyt kaptak. Minden diagramhoz egy-egy példa van felsorolva a tércsoportban való előfordulására.

Némely romboéderes tércsoportban az átlósan orientált Ec, En és Ek síkok mp-típusú N hálókkal fordulnak elő, amelyek egy ortogonális háló háromszoros központozásával írhatók le. Az N háló téglalap alakú hármashálója az ilyen típusú siklósíkokra a 3. ábrán, a (2), (9) és (14) ábrákon látható. A (9) ábrán felismerhető a hasonlóság más n ábrákkal, például a (8) vagy (10) ábrákkal, ha a (9) ábrán az N háló monoklin primitív hálóját átlós siklási vektorokkal tekintjük.

A szimmetriaelemek grafikus szimbólumai

Az ITA83-ban meghatározott és használt meglévő grafikus szimbólumokat az ad-hoc bizottság egy kivétellel megfelelőnek tartja. A helyzet nagyon különbözik a nyomtatott szimbólumokétól, mivel a rajzokon a vetítési irány egy hozzáadott paraméterré válik. Az alábbiakban használt “merőleges vetület” és “párhuzamos vetület” kifejezésekben a merőleges és a párhuzamos a vetítési iránynak a siklósíkhoz viszonyított irányára utal.

Egy Ee sík esetében a 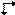szimbólum létezik a merőleges vetületére. Az Ee-sík párhuzamos vetületének létező grafikus szimbólumai azonban ugyanabban a kétértelműségben szenvednek, mint a nyomtatott szimbólumok. Ezek vagy a vetítési iránnyal párhuzamosan, vagy arra merőlegesen fejezik ki a siklóvektort, de a választás önkényes. Ezért egy új szimbólumot javasolunk egy Ee-sík párhuzamos vetületére, nevezetesen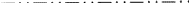

Ee-síkok példái.

Az Fmm2, Fmmm, $Fm\bar 3$ , $Fm\bar 3m$ és $Fm\bar 3c$ (42, 69, 202, 225 és 226 számú) tércsoportok két tengellyel párhuzamos siklósíkjai, valamint a 3. §-ban felsorolt öt tércsoport bizonyos síkjai.

Diagonálisan orientált Ee síkok fordulnak elő az I4mm, I4cm, $I\bar 42m$ , I4/mmm, I4/mcm, $I\bar 43m$ és $Im\bar 3m$ tércsoportokban (Nos. 107, 108, 121, 139, 140, 217 és 229).

Az ITA83-ban mindezek az Ee síkok meglehetősen önkényesen, szaggatott vagy szaggatott vonalként vannak rajzolva a párhuzamos vetületeikben. A 4. ábra az I4cm tércsoport (108. szám) ábráját mutatja, mind az ITA83-ban szereplő módon, mind az új szimbólum használatával.

4. ábra. (a) Az I4cm tércsoport (108. sz.) diagramja az ITA83-ból véve. (b) Ugyanez, a 2. §-ban javasolt grafikus szimbólum használatával módosítva, egy Ee-sík párhuzamos vetületére.

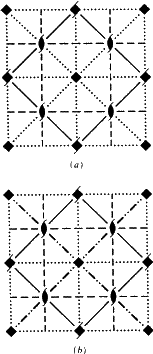
$\begin{figure} \includegraphics {fig4.ps} \end{figure}$

Bár az Ek egy új nyomtatási szimbólum, az ITA83 ábráin az összes Ek siklósíkot kielégítően megrajzolták az Ea/b/c siklósíkoknál használt konvenciókkal. Mint ezekben az esetekben, itt is egyetlen speciális siklási vektor van (a kristálytengelyre merőleges a nettó N-ben, vö. 3. táblázat). Ha ez a vektor például párhuzamos a vetítési síkkal, akkor az Ek-síkot mindig a vonatkozó egyezmény által előírt szaggatott vonalként rajzoljuk meg. Ezért nem javasolunk új grafikai szimbólumot az Ek siklósíkokra.

Példák az Ek síkokra.

Az ITA83 ábráin könnyen megtalálhatók az ilyen síkok, mint csak egy tengellyel párhuzamos és szaggatott vonalként vetített síkok, pl. xxz a P4bm-ben és $P\bar 42_1m$ (100. és 113. szám). Különösen a 3. táblázat pontosan megfelel az Ek és az En síkok között feltüntetett megkülönböztetésnek. Lásd például az R3m és R3c szaggatott és pontozott vonalakat (160. és 161. sz.).

Hermann-Mauguin tércsoport szimbólumok

A tércsoport Hermann-Mauguin (HM) szimbólumában a rácsbetű után megjelenő karakterek eredetileg a csoport generáló műveleteit voltak hivatottak jelölni. Például a b a HM szimbólumban elfoglalt helye szerint orientált síkban való b-csúszó tükrözés volt.

A gyakorlatban a műveletek helyét a népszerű, bár rosszul definiált szimmetriaelemek vették át. Így a b-t a mai terminológiánkban Eb glide-síknak kezdték tekinteni. Ebben az átértelmezésben nincs semmi rossz, kivéve, ha a művelet egy Ee-csúszósíkhoz tartozik. Ha ez például a fenti b-csúszó tükrözésre igaz, akkor a megfelelő orientációban van egy Ee, de nincs Eb-csúszó sík. Ebben az esetben a b nagyon félrevezető karakterré válik. Ettől eltekintve a (b-nek az a-val vagy c-vel szemben adott) torzítás ugyanolyan zavaró, mint az 1. §-ban tárgyalt szimmetriaelem-szimbólumok esetében.

Ezért azt javasoljuk, hogy az ilyen félrevezető a vagy b betűket e-vel helyettesítsük mind az öt HM-szimbólumban, amelyben előfordulnak:

Tércsoport sz.	39	41	64	67	68
Szimbólum az ITA83-ban:	Abm2	Aba2	Cmca	Cmma	Ccca
Új szimbólum:	Aem2	Aea2	Cmce	Cmme	Ccce.

A javasolt új szimbólumok további előnye, hogy e – ellentétben a vagy b-vel – semleges, tehát nem változik meg a tengelyek permutációjánál.

Nyomtatott szimbólumok szimmetria műveletekhez

A nyomtatott szimbólumok teljes készletét tervezte W. Fischer & E. Koch (ITA83, 11.2. §), és széles körben alkalmazták a tércsoport-leírások szimmetriaműveletekre vonatkozó szakaszaiban.

Röviden: minden szimbólum legfeljebb három részből áll. Az első rész egyetlen karakter (néha indexszel együtt), amely a művelet fajtáját írja le. A következő rész(ek) megadja(k) a vonatkozó eltolási vagy transzlációs vektor komponenseit – mindig zárójelben – és a művelet geometriai elemének koordinátáit, ebben a sorrendben.

Az Ad-hoc Bizottság, miután megvizsgálta ezt a rendszert, két módosítást kíván bevezetni a csúszótükrözésekre:

(i) a jelenlegi első karakter helyett (amely lehet a, b, c, n, d vagy g) mindig a g betűt írjuk;

(ii) a csúszásvektor komponenseit (zárójelben) mindig teljes egészében írjuk, különösen az a-, b- vagy c-síkú egyszerű csúszótükrözéseknél, ahol eddig ezeket kihagytuk.

A (i) szabály elnyomja az arra vonatkozó információt, hogy a művelet milyen típusú siklósíkhoz tartozik. Nagyon gyakran ez az információ irreleváns vagy akár zavaró is lehet. Az a/b/c síkok esetében a kitörlés lényeges információt semmisíthet meg, de a veszteséget a (ii) szabály helyreállítja, ahogy az alábbi példában látható.

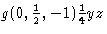Ezek a változtatások elfogadásával a szimbólumok egységessége – a forgatásokra vonatkozó szimbólumok tekintetében is – nagymértékben javul. Például a síkbeli $x = \frac{1}{4}$ csúszó tükrözés szimbóluma a szokatlan $$(0, \frac{1}{2}, -1)$<$ csúszóvektorral, nevezetesen $g(0, \frac{1}{2}, 1) \frac{1}{4}yz$ , most már egybeesik az egyszerű b-csúszó tükrözés szimbólumával. Az ITA83-ban ez utóbbit $b \frac{1}{4} y z$ jelöli, de ez a (ii) szabály által $g(0, \frac{1}{2}, 0) \frac{1}{4} y z$ -re változik.

A fenti szabályok egyformán vonatkoznak a tükörsík elemkészletéhez tartozó csúszótükrözésekre. Így ha egy ilyen művelet eltolási komponense (0, 1, 2), akkor a szimbóluma g(0, 1, 2)-vel kezdődik, nem pedig m(0, 1,2)-vel.

International Tables for Crystallography (1983). Vol. A, szerkesztette: TH. HAHN, különösen az 1.1, 1.3, 1.4, 7 és 11. §§. Dordrecht: Kluwer Academic Publishers.

International Tables for Crystallography (1989). Vol. A, 2., átdolgozott kiadás, szerkesztette: TH. HAHN. Dordrecht: Kluwer Academic Publishers.

WOLFF, P. M. DE, BELOV, N. V., BERTAUT, E. F., BUERGER, M. J., DONNAY, J. D. H., FISCHER, W., HAHN, TH., KOPTSIK, V. A., MACKAY, A. L., WONDRATSCHEK, H., WILSON, A. J. C. & ABRAHAMS, S. C. (1985). Acta Cryst. A41, 278-280.

WOLFF, P. M. DE, BILLIET, Y., DONNAY, J. D. H., FISCHER, W., GALIULIN, R. B., GLAZER, A. M., SENECHAL, M., SHOEMAKER, D. P., WONDRATSCHEK, H., HAHN, TH., WILSON, A. J. C. & ABRAHAMS, S. C. (1989). Acta Cryst. A45, 494-499.

…vektorok. A 3. ábra három (2), (9) és (14) diagramjának c, n és k csúcssík szimbólumait természetesen a 3. táblázat szerint rendeltük hozzá. Az ad hoc bizottság egyik tagja (Wondratschek professzor) úgy gondolja, hogy a (9) diagram n szimbóluma ellentétes az n síkokra vonatkozó hagyományos elképzelésekkel. Javasolja, hogy a (9) diagramhoz egy speciális szimbólumot rendeljünk. Ez a javaslat azonban nem kapott megfelelő támogatást az Ad-hoc Bizottságban.

Szimmetriaelemek és szimmetriaműveletek szimbólumai