La Red de Creencias Bayesiana o Red Bayesiana o Red de Creencias es un Modelo Gráfico Probabilístico (MGP) que representa dependencias condicionales entre variables aleatorias a través de un Gráfico Acíclico Dirigido (DAG).
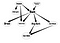
Hoy, trataré de explicar los principales aspectos de las Redes de Creencia, especialmente para aplicaciones que pueden estar relacionadas con el Análisis de Redes Sociales(ARS). Además, mostraré un ejemplo de implementación de este tipo de redes.
¿Para qué usamos las Redes Bayesianas?
Las Redes Bayesianas se aplican en muchos campos. Por ejemplo, el diagnóstico de enfermedades, la búsqueda optimizada en la web, el filtrado de spam, las redes reguladoras de genes, etc. Y esta lista puede ampliarse. El objetivo principal de estas redes es tratar de entender la estructura de las relaciones de causalidad. Para aclarar esto, consideremos un problema de diagnóstico de enfermedades. Con unos síntomas dados y su enfermedad resultante, construimos nuestra red de creencia y cuando llega un nuevo paciente, podemos inferir qué enfermedad o enfermedades puede tener el nuevo paciente proporcionando probabilidades para cada enfermedad. Del mismo modo, estas relaciones de causalidad se pueden construir para otros problemas y aplicar las técnicas de inferencia para obtener resultados interesantes.
Repaso rápido de la probabilidad
Antes de continuar, para refrescar la memoria permítanme darles la definición de propiedad condicional. La probabilidad condicional es la probabilidad de una variable aleatoria cuando se da alguna otra variable aleatoria. Se muestra por
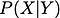
Si estas dos variables aleatorias son dependientes,
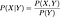
Si son independientes, entonces
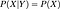
Definición matemática de las redes de creencia
Las probabilidades se calculan en las redes de creencia mediante la siguiente fórmula
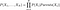
Como se entenderá por la fórmula, para poder calcular la distribución conjunta necesitamos tener las probabilidades condicionales indicadas por la red. Pero además, si tenemos la distribución conjunta, podemos empezar a hacer preguntas interesantes. Por ejemplo, en el primer ejemplo, preguntamos por la probabilidad de «LLUVIA» si «TEMPORADA» es «INVIERNO» y «PERRO LADRA» es «VERDADERO».
Ejemplo de Red de Creencias en Python
Así que, creo que esto es suficiente para la teoría y vamos a ver algún ejemplo real con mi actual lenguaje de programación favorito Python ❤️ Antes de continuar, puedes encontrar el Jupyter Notebook que he escrito aquí.
# create the nodes
season = BbnNode(Variable(0, 'season', ), )
atmos_pres = BbnNode(Variable(1, 'atmos_press', ), )
allergies = BbnNode(Variable(2, 'allergies', ), )
rain = BbnNode(Variable(3, 'rain', ), )
grass = BbnNode(Variable(4, 'grass', ), )
umbrellas = BbnNode(Variable(5, 'umbrellas', ), )
dog_bark = BbnNode(Variable(6, 'dog_bark', ), )
cat_mood = BbnNode(Variable(7, 'cat_mood', ), )
cat_hide = BbnNode(Variable(8, 'cat_hide', ), )bbn = Bbn() \
.add_node(season) \
.add_node(atmos_pres) \
.add_node(allergies) \
.add_node(rain) \
.add_node(grass) \
.add_node(umbrellas) \
.add_node(dog_bark) \
.add_node(cat_mood) \
.add_node(cat_hide) \
.add_edge(Edge(season, allergies, EdgeType.DIRECTED)) \
.add_edge(Edge(season, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(season, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(atmos_pres, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, grass, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, dog_bark, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, cat_mood, EdgeType.DIRECTED)) \
.add_edge(Edge(dog_bark, cat_hide, EdgeType.DIRECTED)) \
.add_edge(Edge(cat_mood, cat_hide, EdgeType.DIRECTED))
Primero describimos nuestros nodos con probabilidades condicionales. Usted debe notar que he omitido algunos posibles valores de estado para la simplicidad. Por ejemplo, la variable estación toma otros valores «primavera» y «otoño». Así que la idea es la misma.
No, comprobemos que nuestro grafo está construido correctamente o no.
with warnings.catch_warnings():
warnings.simplefilter('ignore')
graph = convert_for_drawing(bbn)
pos = nx.nx_agraph.graphviz_layout(graph, prog='neato')plt.figure(figsize=(20, 10))
plt.subplot(121)
labels = dict()
nx.draw(graph, pos=pos, with_labels=True, labels=labels)
plt.title('BBN DAG')
Este fragmento de código daría como resultado el siguiente grafo
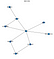
Así que, ya ves que este grafo se ajusta a mi elegante dibujo del principio. Ahora, vamos a hacer un poco de inferencia en esta red de creencia.
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()join_tree.set_observation(ev)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
Este fragmento de código, básicamente, dar evidencia a la red que es la temporada es el invierno con 1,0 de probabilidad. De acuerdo con esta evidencia, cuando hacemos la inferencia, obtenemos los siguientes resultados.
0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.80000
3=sunny|0.20000
--------------------->
4|grass|grass,no_grass
4=grass|0.70000
4=no_grass|0.30000
--------------------->
1|atmos_press|high,low
1=high|0.50000
1=low|0.50000
--------------------->
5|umbrellas|on,off
5=on|0.95200
5=off|0.04800
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.66000
6=not_bark|0.34000
--------------------->
7|cat_mood|good,bad
7=good|0.23000
7=bad|0.77000
--------------------->
8|cat_hide|hide,show
8=hide|0.87150
8=show|0.12850
--------------------->
Cuando añadimos más evidencia, como que el perro no está ladrando
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()ev2 = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('dog_bark')) \
.with_evidence('not_bark', 1.0) \
.build()join_tree.set_observation(ev)
join_tree.set_observation(ev2)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
Obtenemos los siguientes resultados de inferencia
0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.47059
3=sunny|0.52941
--------------------->
4|grass|grass,no_grass
4=grass|0.53529
4=no_grass|0.46471
--------------------->
1|atmos_press|high,low
1=high|0.39706
1=low|0.60294
--------------------->
5|umbrellas|on,off
5=on|0.88941
5=off|0.11059
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.00000
6=not_bark|1.00000
--------------------->
7|cat_mood|good,bad
7=good|0.52647
7=bad|0.47353
--------------------->
8|cat_hide|hide,show
8=hide|0.83162
8=show|0.16838
--------------------->
¿Ves la diferencia? 😆 Muchos valores de probabilidad cambiaron cuando añadimos la evidencia relacionada con los ladridos. Definitivamente es un ejemplo tonto pero agradable para obtener la intuición.
¿Cómo utilizar las Redes Bayesianas en SNA?
Las Redes Bayesianas son herramientas muy poderosas para entender la estructura de las relaciones de causalidad entre las variables. Una vez diseñado el modelo, incluso con un pequeño conjunto de datos, puede decir varias cosas. La pregunta en esta parte es cómo se puede obtener el beneficio de las Redes Bayesianas en SNA. La respuesta no es única, pero empecemos con una idea profunda. En SNA, tratamos de entender la estructura de una red social. Además, intentamos comprender la importancia de los nodos. Pero no sabemos cuáles son los resultados de nuestras métricas de importancia. Este es el punto en el que tienen lugar las redes bayesianas. Por ejemplo, si pensamos que la importancia de un nodo es causada por la Centralidad de Grado y la Centralidad de Enlace, podemos tener la siguiente red.
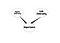
Esta es una Red Bayesiana muy ingenua. Además de determinar la importancia de los nodos, otra aplicación puede ser la búsqueda de algún tipo específico de nodos. Consideremos una Red Social en la que hay algunas personas que son líderes potenciales y quiero buscarlas. Consideremos el siguiente grafo
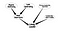
Este grafo un poco más complicado nos ayudará a determinar la incertidumbre de los nodos relacionados con ser un liderazgo.
Otra aplicación sería inferir los enlaces. Los nuevos enlaces pueden inferirse a partir de los existentes. Por ejemplo, a partir de la pertenencia a un grupo en una Red Social, se puede inferir el enlace de pertenencia probable. Lo que quería decir es que podemos modelar un nuevo enlace entre usuarios y grupos considerando los enlaces existentes. Véase el siguiente diagrama del modelo
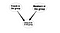
Así pues, estos son algunos ejemplos básicos de cómo se pueden aplicar las Redes Bayesianas en el SNA. Este tema no está muy estudiado, pero creo que puede ser muy útil estudiarlo más.
Conclusión
Lo difícil de las Redes Bayesianas es el diseño. Especialmente, cuando se piensa en SNA, construir el mapeo de la Red Social con una Red Bayesiana es arte que ciencia 😃 Pero una vez que hiciste el trabajo de arte y diseñaste tu modelo muy bien, estas herramientas útiles pueden decirte muchas cosas. Como sabemos, las redes bayesianas se aplican en muchos ámbitos. Han funcionado muy bien en la mayoría de los casos. Por lo tanto, creo firmemente que podemos hacer inferencias muy profundas en las Redes Sociales, también.
Para una mayor investigación con SNA y Redes Bayesianas, por favor, manténgase en sintonía 🚀