Mentre i metodi della sezione precedente sono utili per descrivere e visualizzare dati campione, il vero potere della statistica si rivela quando usiamo i campioni per darci informazioni sulle popolazioni. In questo contesto, una popolazione è l’intera collezione di oggetti di interesse, per esempio, i prezzi di vendita di tutte le case unifamiliari nel mercato immobiliare rappresentato dal nostro set di dati. Vorremmo sapere di più su questa popolazione per aiutarci a prendere una decisione su quale casa comprare, ma l’unico dato che abbiamo è un campione casuale di 30 prezzi di vendita.

Tuttavia, possiamo utilizzare il “pensiero statistico” per trarre inferenze sulla popolazione di interesse analizzando i dati del campione. In particolare, usiamo la nozione di modello – un’astrazione matematica del mondo reale – che adattiamo ai dati del campione. Se questo modello fornisce un adattamento ragionevole ai dati, cioè se può approssimare il modo in cui i dati variano, allora assumiamo che possa anche approssimare il comportamento della popolazione. Il modello fornisce quindi la base per prendere decisioni sulla popolazione, per esempio identificando i modelli, spiegando la variazione e prevedendo i valori futuri. Naturalmente, questo processo può funzionare solo se i dati del campione possono essere considerati rappresentativi della popolazione.

A volte, anche quando sappiamo che un campione non è stato selezionato a caso, possiamo comunque modellarlo. Quindi, potremmo non essere in grado di dedurre formalmente una popolazione dal campione, ma possiamo ancora modellare la struttura sottostante del campione. Un esempio potrebbe essere un campione di convenienza – un campione selezionato più per ragioni di convenienza che per le sue proprietà statistiche. Quando si modellano tali campioni, qualsiasi risultato dovrebbe essere riportato con un’avvertenza sul fatto di limitare qualsiasi conclusione a oggetti simili a quelli nel campione. Un altro tipo di esempio è quando il campione comprende l’intera popolazione. Per esempio, potremmo modellare i dati per tutti i 50 stati degli Stati Uniti d’America per capire meglio qualsiasi modello o associazione sistematica tra gli stati.

Siccome il mondo reale può essere estremamente complicato (nel modo in cui i valori dei dati variano o interagiscono insieme), i modelli sono utili perché semplificano i problemi in modo da poterli capire meglio (e quindi prendere decisioni più efficaci). Da un lato, quindi, abbiamo bisogno che i modelli siano abbastanza semplici da poterli usare facilmente per prendere decisioni, ma dall’altro lato, abbiamo bisogno di modelli che siano abbastanza flessibili da fornire buone approssimazioni a situazioni complesse. Fortunatamente, nel corso degli anni sono stati sviluppati molti modelli statistici che forniscono un equilibrio efficace tra questi due criteri. Uno di questi modelli, che fornisce un buon punto di partenza per i modelli più complicati che considereremo in seguito, è la distribuzione normale.

Da una prospettiva statistica, una distribuzione di probabilità è un modello teorico che descrive come varia una variabile casuale. Per i nostri scopi, una variabile casuale rappresenta i valori dei dati di interesse nella popolazione, per esempio, i prezzi di vendita di tutte le case unifamiliari nel nostro mercato immobiliare. Un modo per rappresentare la distribuzione della popolazione dei valori dei dati è un istogramma, come descritto nella Sezione 1.1. La differenza ora è che l’istogramma mostra l’intera popolazione piuttosto che solo il campione. Poiché la popolazione è molto più grande del campione, i bins dell’istogramma (gli intervalli consecutivi dei dati che comprendono gli intervalli orizzontali per le barre) possono essere molto più piccoli, per esempio, il seguente mostra un istogramma per una popolazione simulata di 1.000 prezzi di vendita.

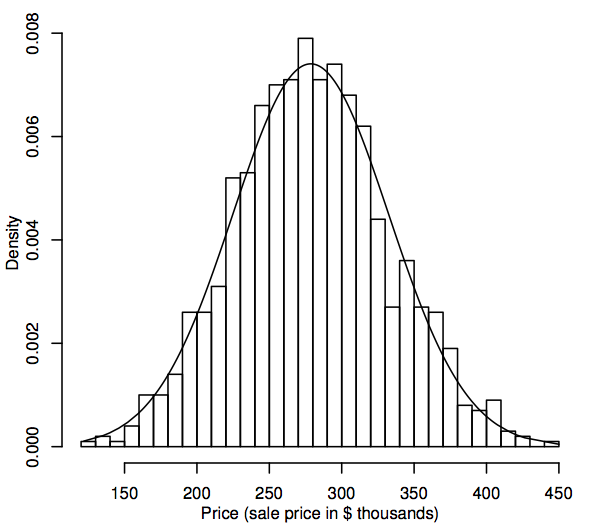
Come la dimensione della popolazione diventa più grande, possiamo immaginare le barre dell’istogramma diventare più sottili e più numerose, finché l’istogramma assomiglia a una curva regolare piuttosto che a una serie di passi. Questa curva liscia è chiamata curva di densità e può essere pensata come la versione teorica dell’istogramma della popolazione. Le curve di densità forniscono anche un modo per visualizzare le distribuzioni di probabilità come la distribuzione normale. Una curva di densità normale è sovrapposta all’istogramma qui sopra. L’istogramma della popolazione simulata segue la curva abbastanza da vicino, il che suggerisce che questa distribuzione della popolazione simulata è abbastanza vicina alla normalità.

Per vedere come una distribuzione teorica può rivelarsi utile per fare inferenze statistiche su popolazioni come quella del nostro esempio sui prezzi delle case, dobbiamo guardare più da vicino la distribuzione normale. Per iniziare, consideriamo una particolare versione della distribuzione normale, la normale standard, rappresentata dalla seguente curva di densità.

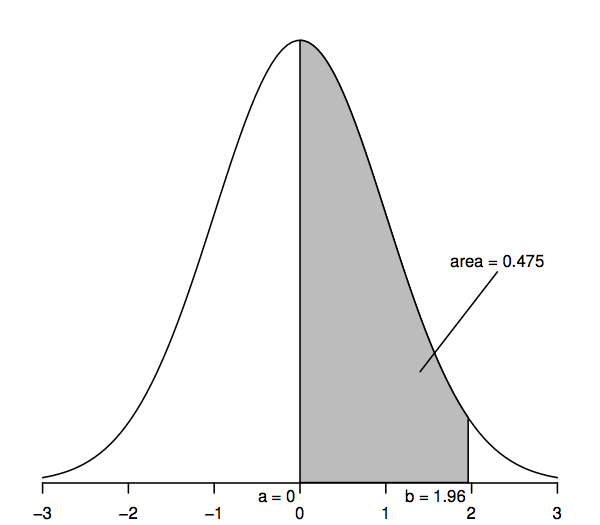
Le variabili casuali che seguono una distribuzione normale standard hanno una media di 0 (quindi la curva è simmetrica intorno a 0, che è sotto il punto più alto della curva) e una deviazione standard di 1 (quindi la curva ha un punto di flesso – dove la curva piega prima in un modo e poi nell’altro – a +1 e -1). La curva di densità normale è talvolta chiamata “curva a campana” poiché la sua forma assomiglia a quella di una campana.

La caratteristica chiave della curva di densità normale che ci permette di fare inferenze statistiche è che le aree sotto la curva rappresentano probabilità. L’intera area sotto la curva è uno, mentre l’area sotto la curva tra un punto sull’asse orizzontale (a, diciamo) e un altro punto (b, diciamo) rappresenta la probabilità che una variabile casuale che segue una distribuzione normale standard sia tra a e b. Così, per esempio, la figura sopra mostra che la probabilità è 0.475 che una variabile casuale normale standard si trovi tra a=0 e b=1.96, poiché l’area sotto la curva tra a=0 e b=1.96 è 0.475.

Possiamo ottenere valori per queste aree o probabilità da una varietà di fonti: tabelle di numeri, calcolatrici, fogli di calcolo o software statistici, siti web e così via. Qui di seguito stampiamo solo alcuni valori selezionati poiché la maggior parte dei calcoli successivi utilizza una generalizzazione della distribuzione normale chiamata “distribuzione t”. Inoltre, piuttosto che aree come quella ombreggiata nella figura sopra, diventerà più utile considerare le “aree di coda” (ad es, a destra del punto b), e così, per coerenza con le successive tabelle di numeri, la seguente tabella permette di calcolare tali aree di coda:

In particolare, l’area di coda superiore a destra di 1,96 è 0,025; ciò equivale a dire che l’area tra 0 e 1,96 è 0,475 (poiché l’intera area sotto la curva è 1 e l’area a destra di 0 è 0,5). Allo stesso modo, l’area a due code, che è la somma delle aree a destra di 1,96 e a sinistra di -1,96, è due volte 0,025, o 0,05.

Come ci aiuta tutto questo a fare inferenze statistiche su popolazioni come quella del nostro esempio dei prezzi delle case? L’idea essenziale è che adattiamo un modello di distribuzione normale ai nostri dati campione e poi usiamo questo modello per fare inferenze sulla popolazione corrispondente. Per esempio, possiamo usare i calcoli di probabilità per una distribuzione normale (come mostrato nella figura sopra) per fare affermazioni di probabilità su una popolazione modellata usando quella distribuzione normale – mostreremo esattamente come farlo nella Sezione 1.3. Prima di farlo, tuttavia, ci fermiamo a considerare un aspetto di questa sequenza inferenziale che può fare o interrompere il processo. Il modello fornisce un’approssimazione abbastanza vicina allo schema dei valori del campione da poter essere sicuri che il modello rappresenti adeguatamente i valori della popolazione? Migliore è l’approssimazione, più affidabili saranno le nostre affermazioni inferenziali.

Abbiamo visto prima come una curva di densità possa essere pensata come un istogramma con un campione molto grande. Quindi un modo per valutare se la nostra popolazione segue un modello di distribuzione normale è quello di costruire un istogramma dai nostri dati campione e determinare visivamente se “sembra normale”, cioè approssimativamente simmetrico e a forma di campana. Questa è una decisione un po’ soggettiva, ma con l’esperienza si dovrebbe scoprire che diventa più facile discernere chiaramente gli istogrammi non normali da quelli che sono ragionevolmente normali. Per esempio, mentre l’istogramma qui sopra sembra chiaramente una curva di densità normale, la normalità dell’istogramma di 30 prezzi di vendita campione nella Sezione 1.1 è meno certa. Una conclusione ragionevole in questo caso sarebbe che mentre questo istogramma campione non è perfettamente simmetrico e a forma di campana, è abbastanza vicino che il corrispondente (ipotetico) istogramma della popolazione potrebbe essere normale.

Un modo alternativo per valutare la normalità è quello di costruire un grafico QQ (grafico quantile-quantile), noto anche come grafico delle probabilità normali, come mostrato qui per i dati sui prezzi delle case:

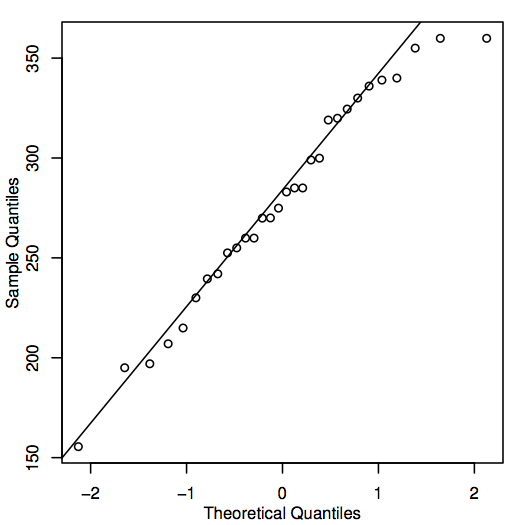
Se i punti nel grafico QQ sono vicini alla linea diagonale, allora i valori corrispondenti della popolazione potrebbero essere normali. Se i punti si trovano generalmente lontano dalla linea, allora la normalità è in discussione. Di nuovo, questa è una decisione un po’ soggettiva che diventa più facile da prendere con l’esperienza. In questo caso, data la dimensione abbastanza piccola del campione, i punti sono probabilmente abbastanza vicini alla linea che è ragionevole concludere che i valori della popolazione potrebbero essere normali.

Esiste anche una varietà di metodi quantitativi per valutare la normalità – vedi Sezione 6.3.