Definizione
Un polinomio nella variabile x è una funzione che può essere scritta nella forma,
dove an, an-1 , …, a2, a1, a0 sono costanti. Chiamiamo il termine che contiene la più alta potenza di x (cioè anxn) il termine principale, e chiamiamo an il coefficiente principale. Il grado del polinomio è la potenza di x nel termine principale. Abbiamo già visto i polinomi di grado 0, 1 e 2 che erano rispettivamente le funzioni costante, lineare e quadratica. Anche i polinomi di grado 3, 4 e 5 hanno nomi speciali: funzioni cubiche, quartiche e quintiche. I polinomi con grado n > 5 sono chiamati semplicemente polinomi di grado n. I nomi delle diverse funzioni polinomiali sono riassunti nella tabella seguente.
| Grado del polinomio | Nome della funzione |
| 0 | Funzione costante |
| 1 | Funzione lineare |
| 2 | Funzione quadratica |
| 3 | Funzione cubica |
| 4 | Funzione quartica |
| 5 | Funzione quintica |
| n (dove n > 5) | polinomio di ennesimo grado |
Alcuni esempi di polinomi includono:
Il comportamento limite dei polinomi
Il comportamento limite di una funzione descrive cosa succede alla funzione come x → ±∞. Il grado di un polinomio e il segno del suo coefficiente iniziale dettano il suo comportamento limite. In particolare,
Questi risultati sono riassunti nella tabella seguente.
Si possono usare queste informazioni per determinare se un polinomio ha grado pari o dispari e se il coefficiente iniziale è positivo o negativo, semplicemente esaminando il suo grafico.
I seguenti grafici di polinomi esemplificano ciascuno dei comportamenti delineati nella tabella precedente.
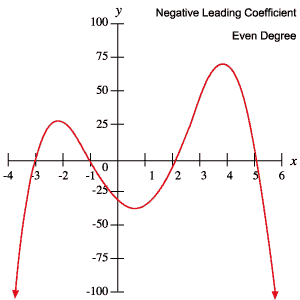
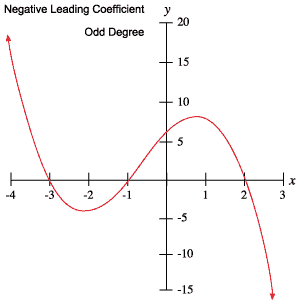
Roots and Turning Points
Il grado di un polinomio ti dice ancora di più sul suo comportamento limite. In particolare, un polinomio di grado n può avere al massimo n radici reali (x-intercette o zeri) contando i multipli. Per esempio, supponiamo di guardare un polinomio di sesto grado che ha 4 radici distinte. Se due delle quattro radici hanno molteplicità 2 e le altre 2 hanno molteplicità 1, sappiamo che non ci sono altre radici perché abbiamo considerato tutte le 6 radici. Questo perché le radici con una molteplicità di due (conosciute anche come radici doppie) sono contate come due radici.
Si noti che un polinomio di grado n non deve necessariamente avere n radici reali – potrebbe averne meno perché ha radici immaginarie. Si noti che un polinomio di grado dispari deve avere almeno una radice reale poiché la funzione si avvicina a – ∞ a un estremo e a + ∞ all’altro; una funzione continua che passa da negativo a positivo deve intersecare l’asse x da qualche parte nel mezzo. Inoltre, un polinomio di n° grado può avere al massimo n – 1 punti di svolta. Un punto di svolta è un punto in cui la funzione passa da crescente a decrescente o da decrescente a crescente, come si vede nella figura qui sotto. Di nuovo, un polinomio di nono grado non deve necessariamente avere n – 1 punti di svolta, potrebbe averne di meno.
Nota di cautela
È importante capire la differenza tra funzioni pari e dispari e polinomi di grado pari e dispari. Qualsiasi funzione, f(x), è pari se,
f(-x) = x,
per tutti gli x nel dominio di f(x), o dispari se,
f(-x) = -x,
per tutti gli x nel dominio di f(x), o né pari né dispari se nessuna delle precedenti sono affermazioni vere.
Un polinomio di grado k, p(x), si dice di grado pari se k è un numero pari e di grado dispari se k è un numero dispari. Ricorda che anche se p(x) ha grado pari, non è necessariamente una funzione pari. Allo stesso modo, se p(x) ha grado dispari, non è necessariamente una funzione dispari.
Utilizziamo i termini pari e dispari anche per descrivere le radici dei polinomi. In particolare, un polinomio p(x) ha radice x = a di molteplicità k (cioè x = a è una radice ripetuta k volte) se (x – a)k è un fattore di p(x). Diciamo che x = a ha molteplicità pari se k è un numero pari e molteplicità dispari se k è un numero dispari.
Dominio e intervallo
Tutti i polinomi hanno lo stesso dominio che consiste di tutti i numeri reali. Anche l’intervallo dei polinomi di grado dispari consiste di tutti i numeri reali. Il campo dei polinomi di grado pari è un po’ più complicato e non possiamo dichiarare esplicitamente il campo di tutti i polinomi di grado pari. Se il coefficiente iniziale è positivo, la funzione si estende fino a + ∞; mentre se il coefficiente iniziale è negativo, si estende fino a – ∞. Questo significa che i polinomi di grado pari con coefficiente iniziale positivo hanno un intervallo in cui ymax denota il massimo globale che la funzione raggiunge. In generale, non è possibile determinare analiticamente i massimi o i minimi dei polinomi.
*****
Nella prossima sezione imparerete la divisione polinomiale, una tecnica usata per trovare le radici di funzioni polinomiali.
Divisione polinomiale