Introduzione

Immagina questo: sei stato incaricato di prevedere il prezzo del prossimo iPhone e ti sono stati forniti dati storici. Questi includono caratteristiche come le vendite trimestrali, le spese mese per mese, e tutta una serie di cose che sono legate al bilancio di Apple. Come scienziato dei dati, quale tipo di problema classificheresti questo come? Dalla previsione delle vendite di un prodotto alla stima del consumo di elettricità delle famiglie, la previsione delle serie temporali è una delle competenze fondamentali che ogni scienziato dei dati deve conoscere, se non padroneggiare. Ci sono una pletora di tecniche diverse che si possono usare, e noi copriremo una delle più efficaci, chiamata Auto ARIMA, in questo articolo.

Prima capiremo il concetto di ARIMA che ci porterà al nostro argomento principale – Auto ARIMA. Per consolidare i nostri concetti, prenderemo un set di dati e lo implementeremo sia in Python che in R.

Tabella dei contenuti

1. Cos’è una serie temporale?
2. Metodi per la previsione delle serie temporali
3. Introduzione all’ARIMA
4. Passi per l’implementazione dell’ARIMA
5. Perché abbiamo bisogno di AutoARIMA?
6. Realizzazione dell’ARIMA automatico (sul set di dati dei passeggeri aerei)
7. Come fa l’ARIMA automatico a selezionare i parametri?

Se avete familiarità con le serie temporali e le sue tecniche (come la media mobile, lo smoothing esponenziale e l’ARIMA), potete saltare direttamente alla sezione 4. Per i principianti, iniziate dalla sezione seguente che è una breve introduzione alle serie temporali e alle varie tecniche di previsione.

Che cos’è una serie temporale?

Prima di imparare le tecniche per lavorare sui dati delle serie temporali, dobbiamo prima capire che cos’è una serie temporale e come è diversa da qualsiasi altro tipo di dati. Ecco la definizione formale di serie temporale – È una serie di punti di dati misurati a intervalli di tempo coerenti. Questo significa semplicemente che particolari valori sono registrati ad un intervallo costante che può essere orario, giornaliero, settimanale, ogni 10 giorni, e così via. Ciò che rende le serie temporali diverse è che ogni punto di dati nella serie dipende dai punti di dati precedenti. Cerchiamo di capire meglio la differenza prendendo un paio di esempi.

Esempio 1:

Supponiamo di avere un set di dati di persone che hanno preso un prestito da una particolare azienda (come mostrato nella tabella qui sotto). Pensate che ogni riga sia collegata alle righe precedenti? Certamente no! Il prestito preso da una persona sarà basato sulle sue condizioni finanziarie e sui suoi bisogni (ci potrebbero essere altri fattori come le dimensioni della famiglia ecc, ma per semplicità stiamo considerando solo il reddito e il tipo di prestito). Inoltre, i dati non sono stati raccolti in un intervallo di tempo specifico. Dipende da quando la società ha ricevuto una richiesta di prestito.

Esempio 2:

Facciamo un altro esempio. Supponiamo di avere un set di dati che contiene il livello di CO2 nell’aria al giorno (screenshot sotto). Sarete in grado di prevedere la quantità approssimativa di CO2 per il giorno successivo guardando i valori dei giorni passati? Beh, certamente. Se osservate, i dati sono stati registrati su base giornaliera, cioè l’intervallo di tempo è costante (24 ore).

A questo punto avrete già avuto un’intuizione – il primo caso è un semplice problema di regressione e il secondo è un problema di serie temporale. Anche se il problema delle serie temporali qui può essere risolto anche usando la regressione lineare, ma questo non è proprio l’approccio migliore perché trascura la relazione dei valori con tutti i relativi valori passati. Vediamo ora alcune delle tecniche comuni usate per risolvere i problemi delle serie temporali.

Metodi per la previsione delle serie temporali

Ci sono diversi metodi per la previsione delle serie temporali e li copriremo brevemente in questa sezione. La spiegazione dettagliata e i codici python per tutte le tecniche menzionate di seguito possono essere trovati in questo articolo: 7 tecniche per la previsione delle serie temporali (con codici python).

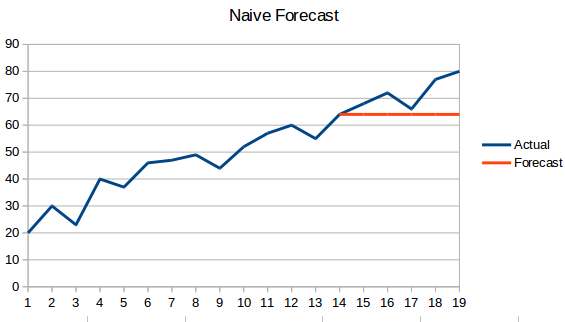
1. Approccio ingenuo: In questa tecnica di previsione, si prevede che il valore del nuovo punto di dati sia uguale al punto di dati precedente. Il risultato sarebbe una linea piatta, poiché tutti i nuovi valori prendono i valori precedenti.
2. Media semplice: Il prossimo valore viene preso come media di tutti i valori precedenti. Le previsioni qui sono migliori di quelle dell'”approccio ingenuo” perché non risulta una linea piatta, ma qui, tutti i valori passati sono presi in considerazione, il che potrebbe non essere sempre utile. Per esempio, quando si chiede di prevedere la temperatura di oggi, si dovrebbe considerare la temperatura degli ultimi 7 giorni piuttosto che quella di un mese fa.
3. Media mobile: Questo è un miglioramento rispetto alla tecnica precedente. Invece di prendere la media di tutti i punti precedenti, la media di ‘n’ punti precedenti è presa per essere il valore previsto.
4. Media mobile ponderata : Una media mobile ponderata è una media mobile dove gli ‘n’ valori passati sono dati pesi diversi.
5. Lisciatura esponenziale semplice: in questa tecnica, vengono assegnati pesi maggiori alle osservazioni più recenti che alle osservazioni del passato lontano.
6. Modello di tendenza lineare di Holt: Questo metodo prende in considerazione la tendenza del set di dati. Per tendenza, intendiamo la natura crescente o decrescente della serie. Supponiamo che il numero di prenotazioni in un hotel aumenti ogni anno, allora possiamo dire che il numero di prenotazioni mostra un trend crescente. La funzione di previsione in questo metodo è una funzione di livello e tendenza.
7. Metodo Holt Winters: Questo algoritmo prende in considerazione sia la tendenza che la stagionalità della serie. Per esempio – il numero di prenotazioni in un hotel è alto nei fine settimana & basso nei giorni feriali, e aumenta ogni anno; esiste una stagionalità settimanale e un trend crescente.
8. ARIMA: ARIMA è una tecnica molto popolare per la modellazione di serie temporali. Descrive la correlazione tra i punti di dati e prende in considerazione la differenza dei valori. Un miglioramento dell’ARIMA è il SARIMA (o ARIMA stagionale). Vedremo l’ARIMA un po’ più in dettaglio nella sezione seguente.

Introduzione all’ARIMA

In questa sezione faremo una rapida introduzione all’ARIMA che sarà utile per capire Auto Arima. Una spiegazione dettagliata di Arima, parametri (p,q,d), trame (ACF PACF) e implementazione è inclusa in questo articolo: Tutorial completo sulle serie temporali.

ARIMA è un metodo statistico molto popolare per la previsione delle serie temporali. ARIMA sta per Auto-Regressive Integrated Moving Averages. I modelli ARIMA lavorano sui seguenti presupposti –

• La serie di dati è stazionaria, il che significa che la media e la varianza non devono variare nel tempo. Una serie può essere resa stazionaria usando la trasformazione logaritmica o differenziando la serie.
• I dati forniti come input devono essere una serie univariata, poiché l’arima usa i valori passati per prevedere i valori futuri.

ARIMA ha tre componenti – AR (termine autoregressivo), I (termine differenziale) e MA (termine medio mobile). Cerchiamo di capire ciascuna di queste componenti –

• Il termine AR si riferisce ai valori passati utilizzati per prevedere il valore successivo. Il termine AR è definito dal parametro ‘p’ in arima. Il valore di ‘p’ è determinato usando il grafico PACF.
• Il termineMA è usato per definire il numero di errori di previsione passati usati per prevedere i valori futuri. Il parametro ‘q’ in arima rappresenta il termine MA. Il grafico ACF è usato per identificare il corretto valore ‘q’.
• Ordine di differenziazione specifica il numero di volte in cui l’operazione di differenziazione viene eseguita sulla serie per renderla stazionaria. Test come ADF e KPSS possono essere usati per determinare se la serie è stazionaria e aiutano a identificare il valore d.

Passi per l’implementazione di ARIMA

I passi generali per implementare un modello ARIMA sono –

1. Caricare i dati: Il primo passo per la costruzione del modello è naturalmente caricare il set di dati
2. Preprocessing: A seconda del set di dati, saranno definite le fasi di pre-elaborazione. Questo includerà la creazione di timestamps, la conversione del tipo di colonna data/ora, rendere la serie univariata, ecc.
3. Rendere la serie stazionaria: Per soddisfare l’ipotesi, è necessario rendere la serie stazionaria. Questo include il controllo della stazionarietà della serie e l’esecuzione delle trasformazioni necessarie
4. Determinare il valore d: Per rendere stazionaria la serie, il numero di volte in cui è stata eseguita l’operazione di differenza sarà preso come valore d
5. Creare i grafici ACF e PACF: Questo è il passo più importante nell’implementazione dell’ARIMA. I grafici ACF PACF sono usati per determinare i parametri di input per il nostro modello ARIMA
6. Determinare i valori p e q: Leggere i valori di p e q dai grafici nel passo precedente
7. Adattare il modello ARIMA: Usando i dati elaborati e i valori dei parametri che abbiamo calcolato dai passi precedenti, adattare il modello ARIMA
8. Prevedere i valori sul set di validazione: Prevedere i valori futuri
9. Calcolare RMSE: Per controllare le prestazioni del modello, controllare il valore RMSE usando le previsioni e i valori effettivi sul set di validazione

Perché abbiamo bisogno dell’Auto ARIMA?

Anche se l’ARIMA è un modello molto potente per la previsione dei dati delle serie temporali, i processi di preparazione dei dati e di regolazione dei parametri finiscono per richiedere molto tempo. Prima di implementare l’ARIMA, è necessario rendere la serie stazionaria e determinare i valori di p e q usando i grafici che abbiamo discusso sopra. Auto ARIMA rende questo compito molto semplice per noi in quanto elimina i passi da 3 a 6 che abbiamo visto nella sezione precedente. Di seguito sono riportati i passi da seguire per implementare l’auto ARIMA:

1. Carica i dati: Questo passo sarà lo stesso. Carica i dati nel tuo notebook
2. Preelaborazione dei dati: L’input dovrebbe essere univariato, quindi lascia perdere le altre colonne
3. Adatta Auto ARIMA: Adatta il modello sulla serie univariata
4. Predice i valori sull’insieme di validazione: Fare previsioni sul set di convalida
5. Calcolare RMSE: Controllare la performance del modello usando i valori predetti contro i valori reali

Abbiamo completamente bypassato la selezione delle caratteristiche p e q come potete vedere. Che sollievo! Nella prossima sezione, implementeremo l’auto ARIMA usando un set di dati giocattolo.

Implementazione in Python e R

Useremo il set di dati International-Air-Passenger. Questo dataset contiene il totale mensile del numero di passeggeri (in migliaia). Ha due colonne – mese e numero di passeggeri. Potete scaricare il dataset da questo link.

#load the datadata = pd.read_csv('international-airline-passengers.csv')#divide into train and validation settrain = datavalid = data#preprocessing (since arima takes univariate series as input)train.drop('Month',axis=1,inplace=True)valid.drop('Month',axis=1,inplace=True)#plotting the datatrain.plot()valid.plot()

#building the modelfrom pyramid.arima import auto_arimamodel = auto_arima(train, trace=True, error_action='ignore', suppress_warnings=True)model.fit(train)forecast = model.predict(n_periods=len(valid))forecast = pd.DataFrame(forecast,index = valid.index,columns=)#plot the predictions for validation setplt.plot(train, label='Train')plt.plot(valid, label='Valid')plt.plot(forecast, label='Prediction')plt.show()

#calculate rmsefrom math import sqrtfrom sklearn.metrics import mean_squared_errorrms = sqrt(mean_squared_error(valid,forecast))print(rms)

output -76.51355764316357

Di seguito il codice R per lo stesso problema:

# loading packageslibrary(forecast)library(Metrics)# reading datadata = read.csv("international-airline-passengers.csv")# splitting data into train and valid setstrain = datavalid = data# removing "Month" columntrain$Month = NULL# training modelmodel = auto.arima(train)# model summarysummary(model)# forecastingforecast = predict(model,44)# evaluationrmse(valid$International.airline.passengers, forecast$pred)

Come fa Auto Arima a selezionare i migliori parametri

Nel codice sopra, abbiamo semplicemente usato il comando .fit() per adattare il modello senza dover selezionare la combinazione di p, q, d. Ma come ha fatto il modello a capire la migliore combinazione di questi parametri? Auto ARIMA prende in considerazione i valori AIC e BIC generati (come potete vedere nel codice) per determinare la migliore combinazione di parametri. I valori AIC (Akaike Information Criterion) e BIC (Bayesian Information Criterion) sono stimatori per confrontare i modelli. Più bassi sono questi valori, migliore è il modello.

Guarda questi link se sei interessato alla matematica dietro AIC e BIC.

Note finali e ulteriori letture

Ho trovato l’auto ARIMA come la tecnica più semplice per eseguire previsioni di serie temporali. Conoscere una scorciatoia è buono, ma avere familiarità con la matematica che c’è dietro è anche importante. In questo articolo ho sfiorato i dettagli di come funziona l’ARIMA, ma assicuratevi di esaminare i link forniti nell’articolo. Per un facile riferimento, ecco di nuovo i link:

• Una guida completa per i principianti alla previsione delle serie temporali in Python
• Tutorial completo sulle serie temporali in R
• 7 tecniche per la previsione delle serie temporali (con codici python)

Vorrei suggerire di mettere in pratica ciò che abbiamo imparato qui su questo problema pratico: Time Series Practice Problem. Puoi anche seguire il nostro corso di formazione creato sullo stesso problema pratico, Previsione delle serie temporali, per darti un vantaggio.