La fase di un’oscillazione o di un’onda è la frazione di un ciclo completo corrispondente a un offset nello spostamento da un punto di riferimento specificato al tempo t = 0. La fase è un concetto del dominio della frequenza o della trasformata di Fourier, e come tale, può essere facilmente compresa in termini di moto armonico semplice. Lo stesso concetto si applica al moto ondoso, visto sia in un punto nello spazio in un intervallo di tempo, sia attraverso un intervallo di spazio in un momento nel tempo. Il moto armonico semplice è uno spostamento che varia ciclicamente, come illustrato di seguito:
File:Simple harmonic motion.png
e descritto dalla formula:

dove A è l’ampiezza di oscillazione, f è la frequenza, t è il tempo trascorso, e 

Si possono notare due potenziali ambiguità:
- Una è che lo spostamento iniziale di
è diverso dalla funzione seno, eppure sembrano avere la stessa “fase”.
- L’angolo variabile nel tempo
o il suo valore modulo
, è anche comunemente chiamato “fase”. Allora non è una condizione iniziale, ma piuttosto una condizione che cambia continuamente.
Il termine fase istantanea è usato per distinguere l’angolo variabile nel tempo dalla condizione iniziale. Ha anche una definizione formale che è applicabile a funzioni più generali e definisce senza ambiguità la fase iniziale di una funzione a t=0. Cioè, seno e coseno hanno intrinsecamente fasi iniziali diverse. Quando non è esplicitamente dichiarato altrimenti, il coseno dovrebbe essere generalmente dedotto. (vedi anche fasore)
Spostamento di fase
Illustrazione dello spostamento di fase. L’asse orizzontale rappresenta un angolo (fase) che aumenta con il tempo.


Per le sinusoidi infinitamente lunghe, un cambiamento in 


 |
 |
{displaystyle =A\cdot \sin(2\pi ft-{begin{matrix}{frac {{2}}end{matrix}}+\theta ),\la cui “fase” è ora  È stato spostato di È stato spostato di  . .
Differenza di faseOnde in fase Out-of-phase waves Sinistra: la parte reale di un’onda piana che si muove dall’alto in basso. A destra: la stessa onda dopo che una sezione centrale ha subito uno spostamento di fase, per esempio passando attraverso un vetro di spessore diverso dalle altre parti. (L’illustrazione a destra ignora l’effetto della diffrazione il cui effetto aumenta su grandi distanze). Due oscillatori che hanno la stessa frequenza e fasi diverse hanno una differenza di fase, e gli oscillatori si dicono fuori fase tra loro. La quantità di cui tali oscillatori sono fuori fase tra loro può essere espressa in gradi da 0° a 360°, o in radianti da 0 a 2π. Se la differenza di fase è di 180 gradi (π radianti), allora i due oscillatori si dicono in antifase. Se due onde interagenti si incontrano in un punto in cui sono in antifase, allora si verifica un’interferenza distruttiva. È comune per le onde elettromagnetiche (luce, RF), acustiche (suono) o di altra energia sovrapporsi nel loro mezzo di trasmissione. Quando ciò accade, la differenza di fase determina se si rafforzano o si indeboliscono a vicenda. La cancellazione completa è possibile per onde con ampiezze uguali. Il tempo è talvolta usato (invece dell’angolo) per esprimere la posizione all’interno del ciclo di un’oscillazione.
Componenti in fase e in quadratura (I&Q)Il termine in fase si trova anche nel contesto dei segnali di comunicazione: e: dove
Coerenza di faseLa coerenza è la qualità di un’onda di mostrare relazioni di fase ben definite in diverse regioni del suo dominio di definizione. In fisica, la meccanica quantistica attribuisce le onde agli oggetti fisici. La funzione d’onda è complessa e poiché il suo modulo quadrato è associato alla probabilità di osservare l’oggetto, il carattere complesso della funzione d’onda è associato alla fase. Poiché l’algebra complessa è responsabile del sorprendente effetto di interferenza della meccanica quantistica, la fase delle particelle è quindi in definitiva legata al loro comportamento quantico. |


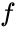 rappresenta una frequenza portante, e
rappresenta una frequenza portante, e

 e
e  rappresentano la possibile modulazione di un’onda portante pura, per esempio:
rappresentano la possibile modulazione di un’onda portante pura, per esempio:  La modulazione altera l’originale
La modulazione altera l’originale  componente della portante, e crea una (nuova)
componente della portante, e crea una (nuova) 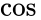 componente, come mostrato sopra. La componente che è in fase con la portante originale è detta componente in fase. L’altra componente, che è sempre 90° (
componente, come mostrato sopra. La componente che è in fase con la portante originale è detta componente in fase. L’altra componente, che è sempre 90° (