La rete di credenza bayesiana o rete bayesiana o rete di credenza è un modello grafico probabilistico (PGM) che rappresenta le dipendenze condizionali tra variabili casuali attraverso un grafico aciclico diretto (DAG).
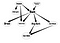
Oggi, cercherò di spiegare gli aspetti principali delle reti di credenza, specialmente per applicazioni che possono essere collegate alla Social Network Analysis (SNA). Inoltre, vi mostrerò un esempio di implementazione di questo tipo di rete.
A cosa servono le Reti Bayesiane?
Le Reti Bayesiane sono applicate in molti campi. Per esempio, la diagnosi delle malattie, la ricerca ottimizzata sul web, il filtraggio dello spam, le reti di regolazione dei geni, ecc. E questa lista può essere estesa. L’obiettivo principale di queste reti è cercare di capire la struttura delle relazioni di causalità. Per chiarire questo, consideriamo un problema di diagnosi di malattia. Con i sintomi dati e la loro malattia risultante, costruiamo la nostra Rete di Credenza e quando arriva un nuovo paziente, possiamo dedurre quale malattia o quali malattie può avere il nuovo paziente fornendo probabilità per ogni malattia. Allo stesso modo, queste relazioni di causalità possono essere costruite per altri problemi e le tecniche di inferenza possono essere applicate per ottenere risultati interessanti.
Passo rapido di probabilità
Prima di continuare, per rinfrescarci la memoria lasciatemi dare la definizione di proprietà condizionata. La probabilità condizionata è la probabilità di una variabile casuale quando è data qualche altra variabile casuale. È dimostrato da
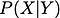
Se queste due variabili casuali sono dipendenti,
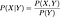
Se sono indipendenti, allora
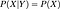
Definizione matematica delle reti di credenza
Le probabilità sono calcolate nelle reti di credenza con la seguente formula
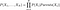
Come si può capire dalla formula, per poter calcolare la distribuzione congiunta abbiamo bisogno di avere le probabilità condizionali indicate dalla rete. Ma inoltre, se abbiamo la distribuzione congiunta, allora possiamo iniziare a fare domande interessanti. Per esempio, nel primo esempio, chiediamo la probabilità di “RAIN” se “SEASON” è “WINTER” e “DOG BARK” è “TRUE”.
Esempio Python di Belief Network
Così, penso che questo basti per la teoria e vediamo qualche esempio reale con il mio attuale linguaggio di programmazione preferito Python ❤️ Prima di continuare, potete trovare il Jupyter Notebook che ho scritto qui.
# create the nodes
season = BbnNode(Variable(0, 'season', ), )
atmos_pres = BbnNode(Variable(1, 'atmos_press', ), )
allergies = BbnNode(Variable(2, 'allergies', ), )
rain = BbnNode(Variable(3, 'rain', ), )
grass = BbnNode(Variable(4, 'grass', ), )
umbrellas = BbnNode(Variable(5, 'umbrellas', ), )
dog_bark = BbnNode(Variable(6, 'dog_bark', ), )
cat_mood = BbnNode(Variable(7, 'cat_mood', ), )
cat_hide = BbnNode(Variable(8, 'cat_hide', ), )bbn = Bbn() \
.add_node(season) \
.add_node(atmos_pres) \
.add_node(allergies) \
.add_node(rain) \
.add_node(grass) \
.add_node(umbrellas) \
.add_node(dog_bark) \
.add_node(cat_mood) \
.add_node(cat_hide) \
.add_edge(Edge(season, allergies, EdgeType.DIRECTED)) \
.add_edge(Edge(season, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(season, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(atmos_pres, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, grass, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, dog_bark, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, cat_mood, EdgeType.DIRECTED)) \
.add_edge(Edge(dog_bark, cat_hide, EdgeType.DIRECTED)) \
.add_edge(Edge(cat_mood, cat_hide, EdgeType.DIRECTED))
Prima abbiamo descritto i nostri nodi con probabilità condizionali. Dovreste notare che ho saltato alcuni possibili valori di stato per semplicità. Per esempio, la variabile stagione prende altri valori “primavera” e “autunno”. Quindi, l’idea è la stessa.
No, controlliamo che la nostra rete sia costruita correttamente o no.
with warnings.catch_warnings():
warnings.simplefilter('ignore')
graph = convert_for_drawing(bbn)
pos = nx.nx_agraph.graphviz_layout(graph, prog='neato')plt.figure(figsize=(20, 10))
plt.subplot(121)
labels = dict()
nx.draw(graph, pos=pos, with_labels=True, labels=labels)
plt.title('BBN DAG')
Questo frammento di codice produrrebbe il seguente grafico
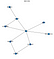
Quindi, vedete che questa rete corrisponde al mio disegno di fantasia all’inizio. Ora, facciamo un po’ di inferenza su questa rete di credenze.
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()join_tree.set_observation(ev)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
Questo frammento di codice dà fondamentalmente la prova alla rete che la stagione è l’inverno con 1,0 di probabilità. In base a questa prova, quando facciamo l’inferenza, otteniamo i seguenti risultati.
0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.80000
3=sunny|0.20000
--------------------->
4|grass|grass,no_grass
4=grass|0.70000
4=no_grass|0.30000
--------------------->
1|atmos_press|high,low
1=high|0.50000
1=low|0.50000
--------------------->
5|umbrellas|on,off
5=on|0.95200
5=off|0.04800
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.66000
6=not_bark|0.34000
--------------------->
7|cat_mood|good,bad
7=good|0.23000
7=bad|0.77000
--------------------->
8|cat_hide|hide,show
8=hide|0.87150
8=show|0.12850
--------------------->
Quando aggiungiamo altre prove, come il fatto che il cane non abbaia
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()ev2 = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('dog_bark')) \
.with_evidence('not_bark', 1.0) \
.build()join_tree.set_observation(ev)
join_tree.set_observation(ev2)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
Abbiamo i seguenti risultati di inferenza
0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.47059
3=sunny|0.52941
--------------------->
4|grass|grass,no_grass
4=grass|0.53529
4=no_grass|0.46471
--------------------->
1|atmos_press|high,low
1=high|0.39706
1=low|0.60294
--------------------->
5|umbrellas|on,off
5=on|0.88941
5=off|0.11059
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.00000
6=not_bark|1.00000
--------------------->
7|cat_mood|good,bad
7=good|0.52647
7=bad|0.47353
--------------------->
8|cat_hide|hide,show
8=hide|0.83162
8=show|0.16838
--------------------->
Vedi la differenza? 😆 Molti valori di probabilità cambiano quando aggiungiamo la prova relativa all’abbaiare. E’ sicuramente un esempio sciocco ma piacevole per avere un’intuizione.
Come usare le reti bayesiane in SNA ?
Le reti bayesiane sono strumenti molto potenti per capire la struttura delle relazioni di causalità tra le variabili. Una volta progettato il modello, anche con un piccolo set di dati, esso può dirvi varie cose. La domanda in questa parte è come si può ottenere il beneficio delle Reti Bayesiane in SNA. La risposta non è unica, ma iniziamo con un’idea profonda. In SNA, cerchiamo di capire la struttura di una rete sociale. Inoltre, cerchiamo di capire l’importanza dei nodi. Ma non sappiamo quali siano i risultati delle nostre metriche di importanza. Questo è il punto in cui intervengono le Reti Bayesiane. Per esempio, se si pensa che l’importanza di un nodo sia causata da Degree Centrality e Link Centrality, si può avere la seguente rete.
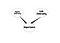
Questa è una Rete Bayesiana molto ingenua. Oltre a determinare l’importanza dei nodi, un’ulteriore applicazione può essere la ricerca di alcuni tipi specifici di nodi. Consideriamo una Rete Sociale in cui ci sono alcune persone che sono potenziali leader e voglio cercarle. Consideriamo il seguente grafico
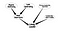
Questa rete un po’ più complicata ci aiuterà a determinare l’incertezza dei nodi relativi ad essere una leadership.
Un’altra applicazione sarebbe dedurre i collegamenti. I nuovi collegamenti possono essere dedotti da quelli esistenti. Per esempio, dall’appartenenza ad un gruppo in una rete sociale, si può dedurre un probabile legame di appartenenza. Quello che volevo dire è che possiamo modellare un nuovo collegamento tra utenti e gruppi considerando i collegamenti esistenti. Vedi il seguente diagramma del modello
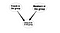
Quindi, questi sono alcuni esempi base di come le Reti Bayesiane possono essere applicate in SNA. Questo argomento non è studiato molto bene ma penso che potrebbe essere molto utile da studiare ulteriormente.
Conclusione
La cosa difficile delle Reti Bayesiane è la progettazione. Specialmente, quando si parla di SNA, costruire la mappatura della Rete Sociale con una Rete Bayesiana è più arte che scienza 😃 Ma una volta che hai fatto il lavoro d’arte e progettato il tuo modello molto bene, questi strumenti pratici possono dirti un sacco di cose. Come sappiamo, le Reti Bayesiane sono applicate in una vasta gamma di aree. Ha funzionato molto bene nella maggior parte dei casi. Pertanto, credo fermamente che possiamo fare inferenze molto profonde anche sulle Reti Sociali.
Per ulteriori indagini con SNA e Reti Bayesiane, rimanete sintonizzati 🚀