(IUCr) Simboli per elementi di simmetria

Acta Cryst. (1992). A48, 727-732

Rapporto finale del Comitato ad hoc dell’Unione Internazionale di Cristallografia sulla nomenclatura di simmetria*

di P. M. DE WOLFF (Presidente), Meermanstraat 126, 2614 AM Delft, Paesi Bassi,

Y. BILLIET, Ecole Nationale d’Ingénieurs, BPW 3038 Sfax, Tunesië,

J. D. H. DONNAY, Dipartimento di Scienze Geologiche, McGill University, 3450 University Street, Montreal, Canada H3A 2A7,

W. FISCHER, Institut für Mineralogie, Petrologie und Kristallographie der Phillips-Universität, Lahnberge, D-3550 Marburg (Lahn), Germania,

R. B. GALIULIN, Institute of Crystallography, Academy of Sciences of Russia, Leninsky Prospekt 59, Moscow 117333, Russia,

A. M. GLAZER, Clarendon Laboratory, Università di Oxford, Parks Road, Oxford OX1 3PU Inghilterra,

TH. HAHN, Institut für Kristallographie, RWTH, Templergraben 55, D-5100 Aachen, Germania,

MARJORIE SENECHAL, Department of Mathematics, Smith College, Northampton, MA 01063, USA,

D. P. SHOEMAKER, Dipartimento di Chimica, Oregon State University, OR 97331, USA,

H. WONDRATSCHEK, Institut für Kristallographie, Universität Karlsruhe, Kaiserstrasse 12, D-7500 Karlsruhe 1, Germania,

A. J. C. WILSON (ex officio, IUCr Commission on International Tables), Crystallographic Data Centre, University Chemistry Laboratory, Lensfield Road, Cambridge CB2 1EW, England

E S. C. ABRAHAMS (ex officio, IUCr Commission on Crystallographic Nomenclature), Department of Physics, Southern Oregon State College, 1250 Siskiyou Boulevard, Ashland, OR 97520-5047, USA

(Ricevuto il 7 novembre 1991; accettato il 9 marzo 1992)

* Nominato il 14 novembre 1984, modificato il 10 agosto 1987 secondo le regole di base descritte in Acta Cryst. (1979), A35, 1072. Rapporto finale accettato il 23 dicembre 1991 dalla Commissione IUCr per la nomenclatura cristallografica e il 9 marzo 1992 dal Comitato esecutivo.

Abstract

Sono proposti simboli stampati nuovi o ridefiniti alla luce della ridefinizione degli elementi di simmetria recentemente accettata. In particolare, la lettera e copre certi piani di scorrimento che finora non avevano un simbolo unico, come quelli chiamati “o a o b”. Si raccomanda l’uso di e nel simbolo di Hermann-Mauguin di cinque diversi gruppi spaziali. Per i piani e proiettati in una direzione parallela al piano, viene proposto un simbolo grafico che rimuove l’ambiguità della loro attuale designazione. La lettera k è proposta per una nuova classe definita di piani di scorrimento che fino ad ora erano senza simbolo specifico. I simboli per le operazioni di simmetria introdotti nelle descrizioni dei gruppi spaziali delle Tavole Internazionali di Cristallografia (1989), Vol. A (Dordrecht: Kluwer Academic Publishers) sono raccomandati per un uso generale, con modifiche solo per le operazioni di riflessione del piano.

Introduzione

Il comitato ad hoc nominato nel 1980 per considerare “i problemi di nomenclatura riguardanti le operazioni di simmetria e gli elementi di simmetria nei gruppi spaziali” ha pubblicato due rapporti intitolati Nomenclatura per famiglie di cristalli, tipi di Bravais-Lattice e classi aritmetiche (de Wolff et al., 1985) e Definition of Symmetry Elements in Space Groups and Point Groups (de Wolff et al., 1989). Come notato nella relazione del 1989, l’unico problema in sospeso riguardante le operazioni di simmetria è quello della scelta dei simboli appropriati, poiché il concetto è chiaro. Una notazione provvisoria è stata adottata nelle Tavole Internazionali per la Cristallografia (1983, 1989), a cui ci si riferisce qui di seguito come ITA83.

Simboli stampati per gli elementi di simmetria

La definizione di elementi di simmetria come data nel Rapporto del 1989 (de Wolff et al.) sarà usata in tutto il presente Rapporto. Qui ripetiamo l’essenza:

Per ogni operazione di simmetria data si definisce il suo elemento geometrico (piano, punto e/o linea). Un elemento di simmetria è la combinazione dell’elemento geometrico di una delle operazioni di simmetria in un dato gruppo di spazio con l’insieme (chiamato ‘insieme di elementi’) di tutte le operazioni di simmetria in quel gruppo di spazio che condividono questo elemento geometrico.

Le definizioni esplicite degli elementi geometrici e le descrizioni degli elementi di simmetria che ne derivano, così come i loro simboli, sono date nelle Tabelle 1 e 2. (Queste sono identiche alle Tabelle 1 e 2 del Rapporto del 1989, tranne che per i piani di scorrimento e sono ripetute qui per completezza, vedi sotto). Ogni elemento di simmetria è rappresentato da un simbolo composto da due caratteri. Il primo carattere è una E maiuscola per tutti gli elementi di simmetria. Serve a mostrare che il simbolo si riferisce a un elemento di simmetria e non, per esempio, a un’operazione di simmetria. Se questo è già chiaro dal contesto, allora la E può essere omessa, ad esempio “un asse 2” invece di “un asse E2”.

Tabella 1. Elementi geometrici delle operazioni di simmetria nei gruppi di punti e nei gruppi spaziali
Operazione di simmetria	Elemento geometrico	Parametri aggiuntivi
Identità	Non richiesto	Nessuno
Traslazione	Non richiesto	Vettore $\mathbf{t}$
Riflessione nel piano A	Piano A	Nessuno
Riflessione di scorrimento =riflessione nel piano A e traslazione parallelo ad A	Piano A	Vettore di scivolamento
Rotazione intorno alla linea b	Linea b	Angolo e senso di rotazione
Rotazione della vite = rotazione intorno alla linea b e traslazione $\mathbf{u}$ parallela a b	Linea b	Angolo e senso del vettore vite di rotazione
Rotoinversione = rotazione intorno alla linea b e inversione attraverso il punto P su b	Line b e punto P su b	Angolo (non uguale a $\pi$ ) e senso di rotazione
Inversione attraverso il punto P	Punto P	Nessuno

Il simbolo Eg elencato nel Rapporto 1989 può essere usato per i piani di scorrimento se si vuole semplicemente mostrare che l’elemento di simmetria è un piano di scorrimento. D’altra parte, se appartiene a uno dei tipi speciali che sono stati a lungo denotati da una lettera appropriata (a, b, c, n o d; cfr. ITA83), allora quella lettera sostituisce g in Eg.

Tabella 2. Elementi di simmetria nei gruppi di punti e nei gruppi spaziali
Nome dell’elemento di simmetria	Simbolo	Elemento geometrico	Operazione di definizione (d.o.)	Operazioni nell’insieme degli elementi
Piano specchio	Em	Piano A	Riflessione in A	D.o. e i suoi equivalenti complanari*
Piano di scorrimento	Eg $\ddag$	Piano A	Riflessione in A, 2v (non v) una traslazione reticolare	D.o. e i suoi equivalenti complanari*
Asse di rotazione	En	Linea b	Rotazione intorno a b, angolo $2\pi/n$ ,n = 2, 3, 4 o 6	1a,, (n – 1)° potenze di d.o. e i loro equivalenti coassiali $\dag$
Asse della vite	Enj	Linea b	Rotazione della vite intorno a b, angolo $2\pi/n$ , u =j/n volte la più breve traslazione lungo b, vite destra; n = 2, 3, 4 o 6, $j=1,\punti,(n-1)$	1°,,(n – 1)° potenze di d.o. e i loro equivalenti coassiali $\dag$
Asse di rotazione	$E\bar n$	Linea b e punto P su b	Rotoinversione: rotazione su b, angolo $2\pi/n$ , e inversione attraverso P; n = 3, 4 o 6	D.o. e il suo inverso
Centro	$E\bar 1$	Punto P	Inversione attraverso P	D.o. solo

* Cioè tutte le riflessioni di scorrimento con lo stesso piano di riflessione, con i vettori di scorrimento che differiscono da quello del d.o. (preso per zero per una riflessione) di un vettore di traslazione del reticolo.
$\dag$ Ovvero, tutte le rotazioni e le rotazioni a vite con lo stesso asse b, lo stesso angolo e senso di rotazione e lo stesso vettore vite $\mathbf{u}$ (zero per una rotazione) fino a un vettore di traslazione del reticolo.
$\ddag$ In Eg, g è sostituito da a, b, c, n, d, e o k per specifici tipi di piani di scorrimento, cfr. §2.

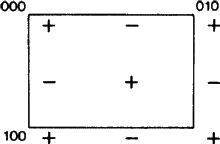
Un nuovo importante aspetto dei simboli come Eb può, tuttavia, essere sottolineato. Secondo ITA83, denotare un piano con b significava semplicemente che una riflessione di scorrimento nel piano con una componente di scorrimento b/2 lungo l’asse b è un’operazione di simmetria. Questa definizione si applica certamente alla situazione rappresentata nella Fig. 1.

Fig. 1. (Dopo W. Fischer.) L’insieme degli elementi di un piano Eb-glide, mostrato come un insieme di punti sopra (+) e sotto (-) il piano prodotto dalle riflessioni glide nel piano, partendo per esempio dal segno + in alto a sinistra. La rete N di traslazioni parallele al piano (+ $\cdots$ + vettori) è indicata da una maglia, che in questo caso è rettangolare. Entrambe le coppie di spigoli sono parallele agli assi del cristallo. C’è una riflessione di scorrimento con il suo vettore di scorrimento (+ $\cdots$ -) lungo l’asse b.

\begin{figure} \includere la grafica {fig1.ps} \La figura 1 è adattata, come le figure 2 e 3, da una serie di figure simili disegnate dal membro del comitato ad hoc W. Fischer come inventario di tutti i tipi di piani di scorrimento. Sebbene l’insieme sia stato presentato al Comitato nel 1980, molto prima che uscisse il Rapporto del 1989, ciascuna delle sue figure mostra precisamente l'”insieme degli elementi” del piano di discesa come definito in quel Rapporto (cfr. il riassunto sopra). Per un piano di scorrimento, l’insieme degli elementi consiste in tutte le riflessioni di scorrimento che hanno il piano come loro elemento geometrico comune. La loro azione è mostrata in proiezione su questo piano. Dalla posizione di partenza di ogni segno +, ogni segno – risulta da una delle riflessioni di scorrimento dell’insieme. Tutti questi sono mostrati all’interno di una maglia elementare del modello periodico bidimensionale risultante di segni + e -.

Faremo spesso riferimento alla rete N formata da tutte le traslazioni parallele al piano; questa rete è facilmente visualizzabile guardando solo i segni +. Questi vettori sono da distinguere nettamente dai vettori che collegano un segno + con un qualsiasi segno -, ognuno dei quali è il vettore planare di una riflessione planare appartenente all’insieme degli elementi.

Il nuovo aspetto sorge perché, in alcuni casi, per la definizione ITA83, il piano b-glide è anche un piano a-glide; vedi Fig. 2. Chiaramente questo accade solo se la rete N è centrata ortogonalmente, perché allora la planata a può essere cambiata in una planata b (e viceversa) aggiungendo una traslazione di centraggio. La pratica finora è stata quella di chiamare tale piano di scorrimento arbitrariamente o a o b, causando così una distorsione ingiustificata e una mancanza di unicità in questi simboli. Pertanto, proponiamo che il caso della Fig. 2 sia coperto da un simbolo separato.

Fig. 2. (Dopo W. Fischer.) L’insieme degli elementi di un piano Ee-glide. Cfr. didascalia della Fig. 1. Si noti che la rete N qui è centrata ortogonalmente.

$\begin{figure} \includegraphics {fig2.ps}$

Lo scopo di questo simbolo dovrebbe quindi essere esteso ai piani di scorrimento con orientamento diagonale, cioè paralleli ad un solo asse del cristallo, a condizione che il piano di scorrimento abbia un vettore di scorrimento lungo quell’asse e che la rete N sia centrata ortogonalmente. Per tali piani non c’è l’ambiguità della scelta casuale a-b di cui sopra, ma la portata estesa del nuovo simbolo è in linea con quella di tutti i simboli esistenti (cioè a, b, c, n e d). Ognuno di questi è usato per un piano di scorrimento con uno e due assi di cristallo nella rete N, cfr. Fig. 3.

La lettera e è proposta per il nuovo simbolo. Così, Ee si applicherà ai piani di scorrimento con reti centrate ortogonali N e almeno un vettore di scorrimento lungo un asse di cristallo. Un nuovo criterio è quindi necessario: l’orientamento dei vettori di scorrimento rispetto agli assi convenzionali del cristallo. Poiché questi ultimi sono lungo le direzioni di simmetria, mentre ogni piano di scorrimento è parallelo a un piano speculare del reticolo, non è sorprendente che ci sia sempre almeno un asse convenzionale del cristallo in N. Se c’è solo un tale asse, allora perpendicolarmente ad esso c’è sempre un’altra traslazione in N.

Il nuovo simbolo e e i vecchi simboli a, b, c, d, n saranno ora ridefiniti in termini di questo nuovo criterio e del tipo Bravais di rete N. Questa rete è monoclina o ortogonale o tetragonale primitiva (mp o op o tp) o ortogonale centrata (oc). Solo le reti N di tipo oc consentono un piano Ee-glide. Il simbolo En è applicabile alle reti N del tipo Bravais mp o op, mentre Ed è per le reti N di tipo oc (come dichiarato in una nota a piè di pagina alla Tabella 1.3 in ITA83: “I piani di scorrimento d si verificano solo nei gruppi spaziali F ortorombici, nei gruppi spaziali I tetragonali, e nei gruppi spaziali I ed F cubici. Si presentano sempre in coppia con vettori di scorrimento alternati”). In contrasto con i piani Ea, Eb, Ec ed Ee, tuttavia, per i piani En ed Ed non c’è alcun vettore di scorrimento né parallelo né perpendicolare a un asse convenzionale in N.

Le seguenti definizioni dei piani di scorrimento dei tipi sopra elencati sono riassunte nelle righe (i) e (ii) della Tabella 3, e più esplicitamente nella Fig. 3.

Tabella 3. Simboli stampati per tipi speciali di piani di scorrimento
Numero di vettori di scorrimento paralleli o perpendicolari agli assi del cristallo nella rete N	Tipo di Bravais della rete N
Il simbolo è determinato da due criteri. Un criterio è il tipo di Bravais (mp, op, tp o oc) della rete N formata dalle traslazioni di simmetria parallele al piano considerato. Questa rete contiene sempre almeno un asse di cristallo convenzionale.* L’altro criterio si riferisce all’orientamento dei vettori di scorrimento rispetto a tali assi.
	m, op, tp	oc
(i) Uno o due paralleli	Ec(Ea, Eb)	Ee
(ii) Nessuna parallela, nessuna perpendicolare	En	Ed
(iii) Nessuna parallela, una perpendicolare	Ek	–

* Come definito in ITA83, § 9.1; tuttavia, per i gruppi spaziali romboedrici, qui si usano solo gli assi esagonali.

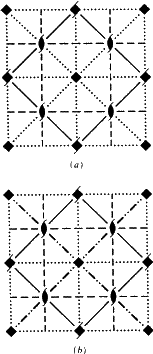
Tutti i restanti piani di scorrimento erano precedentemente senza simbolo specifico. Ognuno di essi ha un orientamento diagonale (un solo asse di cristallo convenzionale nella rete N). Tra le riflessioni di scivolamento nel loro insieme di elementi, non ce n’è nessuna con un vettore di scivolamento lungo quell’asse. Tuttavia, un vettore di scorrimento è (per simmetria) perpendicolare ad esso. Un simbolo sembra desiderabile, così ancora una volta viene proposta una nuova lettera: k. Il nuovo simbolo Ek è brevemente definito nella riga (iii) della Tabella 3 ed è completamente illustrato nel blocco inferiore della Fig. 3. Alcuni esempi sono dati in §2.

Fig. 3. (Adattato dai disegni di W. Fisher.) Tutti i possibili aspetti degli insiemi di elementi dei piani di scorrimento mostrati come in Fig. 1, ma indipendenti dalle etichette degli assi. I diagrammi sono raggruppati in colonne guidate dal simbolo di tipo Bravais-net (linea superiore) delle loro reti N, cfr. tabella 3. Gli altri criteri di quella tabella sono verificati guardando prima le linee doppie che mostrano le direzioni degli assi dei cristalli nel piano. Un bordo (verticale) della rete di N indicata è sempre scelto lungo tale asse. L’altro bordo è orizzontale tranne che in (1) e (8). Per i diagrammi (1), $\punti$ ,(5), il simbolo del piano di scorrimento è l’etichetta a, b o c dell’asse verticale; per gli altri è la lettera cerchiata nel blocco delineato che contiene il diagramma. Si notino i vettori di scorrimento verticali nei diagrammi (1), $\punti$ ,(7), quelli orizzontali in (6), (7), (14), (15) e l’assenza di entrambi in (8),

,(13). Un esempio di occorrenza è dato sotto ogni diagramma dal simbolo del gruppo spaziale e dalla terna di coordinate del piano.

\begin{figure} \includegraphics {fig3.ps} \Nella Fig. 3, l’inventario di Fischer di tutti i tipi di piano di scorrimento è mostrato in modo abbreviato – anche se ancora completo – in cui è stato dato più risalto grafico agli assi del cristallo. Per ogni diagramma, un esempio della sua occorrenza in un gruppo spaziale è elencato.

In alcuni gruppi spaziali romboedrici, i piani Ec, En ed Ek orientati diagonalmente si verificano con reti di tipo mp N che possono essere descritte da una triplice centratura di una rete ortogonale. Una tripla maglia rettangolare della rete N è mostrata per questi tipi di piani di scorrimento in Fig. 3, diagrammi (2), (9) e (14). Nel diagramma (9), la somiglianza con altri diagrammi n come (8) o (10) è riconosciuta se in (9) si considera una maglia primitiva monoclina della rete N con vettori di scorrimento diagonali.

Simboli grafici per elementi di simmetria

I simboli grafici esistenti come definiti e usati in ITA83 sono considerati adeguati dal Comitato Ad-hoc con una eccezione. La situazione è molto diversa da quella dei simboli stampati perché nei disegni la direzione di proiezione diventa un parametro aggiunto. Nei termini `proiezione perpendicolare’ e `proiezione parallela’ usati di seguito, perpendicolare e parallelo si riferiscono all’orientamento della direzione di proiezione rispetto al piano di scorrimento.

Per un piano Ee il simbolo esiste per la sua proiezione perpendicolare. I simboli grafici esistenti per la proiezione parallela di un piano di scorrimento Ee, tuttavia, soffrono della stessa ambiguità dei simboli stampati. Essi esprimono il vettore di scorrimento sia parallelo che perpendicolare alla direzione di proiezione, ma la scelta è arbitraria. Pertanto, viene proposto un nuovo simbolo per la proiezione parallela di un piano di scorrimento Ee, cioè

Esempi di piani Ee.

Tutti i piani di scorrimento paralleli a due assi nei gruppi spaziali Fmm2, Fmmm, $Fm\bar 3$ , $Fm\bar 3m$ e $Fm\bar 3c$ (nn. 42, 69, 202, 225 e 226), così come certi piani nei cinque gruppi spaziali elencati nel §3.

I piani Ee orientati diagonalmente si verificano nei gruppi spaziali I4mm, I4cm, $I\bar 42m$ , I4/mmm, I4/mcm, $I\bar 43m$ e $Im\bar 3m$ (nn. 107, 108, 121, 139, 140, 217 e 229).

In ITA83 tutti questi piani Ee sono disegnati piuttosto arbitrariamente come linee punteggiate o tratteggiate nelle loro proiezioni parallele. La Fig. 4 mostra il diagramma del gruppo spaziale I4cm (No. 108), sia come mostrato in ITA83 che con l’uso del nuovo simbolo.

Fig. 4. (a) Diagramma del gruppo spaziale I4cm (n. 108) tratto da ITA83. (b) Lo stesso, modificato utilizzando il simbolo grafico proposto nel § 2, per la proiezione parallela di un piano Ee.

$\begin{figure} \includegraphics {fig4.ps} \fine{figura}$

Anche se Ek è un nuovo simbolo di stampa, nei diagrammi di ITA83 tutti i piani planari Ek sono stati disegnati in modo soddisfacente con le stesse convenzioni usate per i piani planari Ea/b/c. Come in questi casi, c’è un unico vettore di planata speciale (perpendicolare all’asse del cristallo nella rete N, cfr. tabella 3). Quando questo vettore è, per esempio, parallelo al piano di proiezione, il piano Ek è sempre disegnato come la linea tratteggiata prescritta dalla relativa convenzione. Pertanto, nessun nuovo simbolo grafico viene proposto per i piani di scorrimento Ek.

Esempi di piani Ek.

Tali piani si trovano facilmente nei diagrammi di ITA83 come piani paralleli a un solo asse e proiettati come linee tratteggiate, per esempio xxz in P4bm e $P\bar 42_1m$ (nn. 100 e 113). In particolare, la tabella 3 è esattamente conforme alla distinzione indicata tra i piani Ek e En. Si vedano, per esempio, le linee tratteggiate e tratteggiate per R3m e R3c (nn. 160 e 161).

Simboli dei gruppi spaziali di Hermann-Mauguin

I caratteri che appaiono dopo la lettera di reticolo nel simbolo di Hermann-Mauguin (HM) di un gruppo spaziale erano originariamente destinati a rappresentare operazioni generatrici del gruppo. Per esempio, b era una riflessione b-glide in un piano orientato secondo la sua posizione nel simbolo HM.

In pratica, gli elementi di simmetria popolari anche se mal definiti presero il posto delle operazioni. Così, b venne ad essere visto come un piano di scorrimento, Eb nella nostra terminologia attuale. Non c’è nulla di male in questa reinterpretazione, tranne quando l’operazione appartiene a un piano di scorrimento Ee. Se questo vale, per esempio, per la riflessione b-glide di cui sopra, allora c’è un piano Ee ma nessun piano Eb-glide nell’orientamento corrispondente. In questo caso, b diventa un carattere molto fuorviante. A parte questo, la distorsione (data a b rispetto ad a o c) è altrettanto inquietante che nel caso dei simboli degli elementi di simmetria trattati nel §1.

Perciò, si propone di sostituire tali lettere fuorvianti a o b con e in tutti i cinque simboli HM in cui si presentano:

Gruppo spaziale No.	39	41	64	67	68
Simbolo in ITA83:	Abm2	Aba2	Cmca	Cmma	Ccca
Nuovo simbolo:	Aem2	Aea2	Cmce	Cmme	Ccce.

Un ulteriore vantaggio dei nuovi simboli proposti è che e – a differenza di a o b – è neutro e quindi non viene cambiato con la permutazione degli assi.

Simboli stampati per operazioni di simmetria

Un set completo di simboli stampati è stato progettato da W. Fischer & E. Koch (ITA83, §11.2) ed è stato ampiamente applicato nelle sezioni delle operazioni di simmetria delle descrizioni dei gruppi spaziali.

In breve, ogni simbolo consiste di un massimo di tre parti. La prima parte è un singolo carattere (a volte con un indice) che descrive il tipo di operazione. La parte o le parti seguenti danno le componenti di qualsiasi vettore di spostamento o traslazione pertinente – sempre tra parentesi – e le coordinate dell’elemento geometrico dell’operazione, in quest’ordine.

Il Comitato ad hoc, dopo aver considerato questo sistema, desidera introdurre due modifiche per le riflessioni di scorrimento:

(i) invece dell’attuale primo carattere (che può essere a, b, c, n, d o g), scrivere sempre la lettera g;

(ii) scrivere sempre le componenti del vettore di scorrimento (tra parentesi) per intero, in particolare per le semplici riflessioni di scorrimento nei piani a, b o c dove erano precedentemente omesse.

La regola (i) sopprime le informazioni sul tipo di piano di scorrimento a cui appartiene l’operazione. Molto spesso queste informazioni sono irrilevanti o addirittura confuse. Per i piani a/b/c la soppressione può distruggere informazioni essenziali, ma la perdita è ripristinata dalla regola (ii) come mostrato nell’esempio qui sotto.

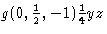Adottando queste modifiche, l’uniformità dei simboli – anche rispetto a quelli per le rotazioni – è notevolmente migliorata. Per esempio, il simbolo della riflessione di scorrimento nel piano $x = \frac{1}{4}$ , con l’insolito vettore di scorrimento $(0, \frac{1}{2}, -1)$ , cioè $g(0, \frac{1}{2}, 1) \frac{1}{4}yz$ , ora è in linea con quello per una semplice riflessione b-glide. In ITA83 quest’ultima era denotata da $b \frac{1}{4} y z$ , ma questa è cambiata dalla regola (ii) in $g(0, \frac{1}{2}, 0) \frac{1}{4} y z$ .

Le regole precedenti si applicano ugualmente alle riflessioni di scivolamento appartenenti all’insieme degli elementi di un piano speculare. Così, se la componente di spostamento di una tale operazione è (0, 1, 2), allora il suo simbolo inizia con g(0, 1, 2), non con m(0, 1,2).

Tabelle internazionali di cristallografia (1983). Vol. A, a cura di TH. HAHN, specialmente i §§ 1.1, 1.3, 1.4, 7 e 11. Dordrecht: Kluwer Academic Publishers.

Tabelle internazionali per la cristallografia (1989). Vol. A, 2a, rivista, ed., a cura di TH. HAHN. Dordrecht: Kluwer Academic Publishers.

WOLFF, P. M. DE, BELOV, N. V., BERTAUT, E. F., BUERGER, M. J., DONNAY, J. D. H., FISCHER, W., HAHN, TH., KOPTSIK, V. A., MACKAY, A. L., WONDRATSCHEK, H., WILSON, A. J. C. & ABRAHAMS, S. C. (1985). Acta Cryst. A41, 278-280.

WOLFF, P. M. DE, BILLIET, Y., DONNAY, J. D. H., FISCHER, W., GALIULIN, R. B., GLAZER, A. M., SENECHAL, M., SHOEMAKER, D. P., WONDRATSCHEK, H., HAHN, TH., WILSON, A. J. C. & ABRAHAMS, S. C. (1989). Acta Cryst. A45, 494-499.

…vettori. I simboli del piano di scorrimento c, n e k per i tre diagrammi (2), (9) e (14) della Fig. 3 sono stati ovviamente assegnati secondo la Tabella 3. Un membro del comitato ad hoc (il professor Wondratschek) pensa che il simbolo n per il diagramma (9) sia in conflitto con le nozioni tradizionali sugli n piani. Egli propone l’assegnazione di un simbolo speciale al diagramma (9). Questa proposta, tuttavia, non ha ricevuto un sostegno adeguato all’interno del Comitato Ad-hoc.

Simboli per elementi di simmetria e operazioni di simmetria