In questo articolo, spiegherò come le convoluzioni 2D sono implementate come moltiplicazioni di matrici. Questa spiegazione è basata sugli appunti del CS231n Reti Neurali Convoluzionali per il Riconoscimento Visivo (Modulo 2). Presumo che il lettore abbia familiarità con il concetto di operazione di convoluzione nel contesto di una rete neurale profonda. In caso contrario, questo repo ha una relazione ed eccellenti animazioni che spiegano cosa sono le convoluzioni. Il codice per riprodurre i calcoli in questo articolo può essere scaricato qui.
Piccolo esempio
Supponiamo di avere un’immagine 4 x 4 a canale singolo, X, e che i suoi valori di pixel siano i seguenti:

Supponiamo inoltre di definire una convoluzione 2D con le seguenti proprietà:

Questo significa che ci saranno 9 patch di immagine 2 x 2 che saranno moltiplicate per elementi con la matrice W, così:

Queste patch di immagine possono essere rappresentate come vettori colonna 4-dimensionali e concatenate per formare una singola matrice 4 x 9, P, così:

Nota che l’i-esima colonna della matrice P è in realtà l’i-esima patch di immagini in forma di vettore colonna.
La matrice dei pesi per lo strato di convoluzione, W, può essere appiattita in un vettore di righe a 4 dimensioni, K, così:
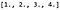
Per eseguire la convoluzione, moltiplichiamo prima la matrice K con P per ottenere un vettore di riga a 9 dimensioni (matrice 1 x 9) che ci dà:

Poi rimodelliamo il risultato di K P nella forma corretta, che è una matrice 3 x 3 x 1 (dimensione del canale per ultima). La dimensione del canale è 1 perché abbiamo impostato i filtri di uscita a 1. L’altezza e la larghezza è 3 perché secondo le note CS231n:

Questo significa che il risultato della convoluzione è:
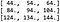
Che si verifica se eseguiamo la convoluzione usando le funzioni integrate di PyTorch (vedi il codice che accompagna questo articolo per i dettagli).
Esempio più grande
L’esempio della sezione precedente presuppone una singola immagine e che i canali di uscita della convoluzione siano 1. Cosa cambierebbe se rilassassimo queste assunzioni?
Assumiamo che il nostro input alla convoluzione sia un’immagine 4 x 4 con 3 canali con i seguenti valori di pixel:

Per quanto riguarda la nostra convoluzione, la imposteremo per avere le stesse proprietà della sezione precedente tranne che i suoi filtri di uscita sono 2. Questo significa che la matrice iniziale dei pesi, W, deve avere forma (2, 2, 2, 3) cioè (filtri di uscita, altezza del kernel, larghezza del kernel, canali dell’immagine di ingresso). Impostiamo W per avere i seguenti valori:

Nota che ogni filtro di uscita avrà il proprio kernel (che è il motivo per cui abbiamo 2 kernel in questo esempio) e il canale di ogni kernel è 3 (poiché l’immagine di ingresso ha 3 canali).
Siccome stiamo ancora convolvendo un kernel 2 x 2 su un’immagine 4 x 4 con 0 zero-padding e stride 1, il numero di patch dell’immagine è ancora 9. Tuttavia, la matrice delle patch di immagine, P, sarà diversa. Più specificamente, l’i-esima colonna di P sarà la concatenazione dei valori del 1°, 2° e 3° canale (come vettore di colonna) corrispondente alla patch di immagine i. P sarà ora una matrice 12 x 9. Le righe sono 12 perché ogni patch di immagine ha 3 canali e ogni canale ha 4 elementi poiché abbiamo impostato la dimensione del kernel a 2 x 2. Ecco come appare P:

Come per W, ogni kernel sarà appiattito in un vettore di righe e concatenato in ordine di riga per formare una matrice 2 x 12, K. L’i-esima riga di K è la concatenazione dei valori del 1°, 2° e 3° canale (in forma di vettore di riga) corrispondente all’i-esimo kernel. Ecco come sarà K:

Ora non resta che eseguire la moltiplicazione della matrice K P e rimodellarla nella forma corretta. La forma corretta è una matrice 3 x 3 x 2 (dimensione del canale per ultima). Ecco il risultato della moltiplicazione:

Ed ecco il risultato dopo averla rimodellata in una matrice 3 x 3 x 2:

Che ancora una volta si verifica se eseguiamo la convoluzione usando le funzioni incorporate di PyTorch (vedi il codice di accompagnamento di questo articolo per i dettagli).
E allora?
Perché dovremmo preoccuparci di esprimere le convoluzioni 2D in termini di moltiplicazioni di matrici? Oltre ad avere un’implementazione efficiente adatta all’esecuzione su una GPU, la conoscenza di questo approccio ci permetterà di ragionare sul comportamento di una rete neurale convoluzionale profonda. Per esempio, He et. al. (2015) hanno espresso le convoluzioni 2D in termini di moltiplicazioni di matrici che hanno permesso loro di applicare le proprietà delle matrici/vettori casuali per argomentare una migliore routine di inizializzazione dei pesi.
Conclusione
In questo articolo, ho spiegato come eseguire le convoluzioni 2D utilizzando le moltiplicazioni di matrici percorrendo due piccoli esempi. Spero che questo sia sufficiente per generalizzare a dimensioni di immagini di input e proprietà di convoluzione arbitrarie. Fatemi sapere nei commenti se qualcosa non è chiaro.
Convoluzione 1D
Il metodo descritto in questo articolo si generalizza anche alle convoluzioni 1D.
Per esempio, supponiamo che il tuo input sia un vettore 12-dimensionale a 3 canali come questo:

Se impostiamo la nostra convoluzione 1D per avere i seguenti parametri:
- dimensione del kernel: 1 x 4
- canali di uscita: 2
- stride: 2
- padding: 0
- bias: 0
Allora i parametri dell’operazione di convoluzione, W, saranno un tensore con forma (2 , 3, 1, 4). Impostiamo W per avere i seguenti valori:

In base ai parametri dell’operazione di convoluzione, la matrice di patch “immagine” P, avrà una forma (12, 5) (5 patch immagine dove ogni patch immagine è un vettore 12-D poiché una patch ha 4 elementi attraverso 3 canali) e sarà come questa:

In seguito, appiattiamo W per ottenere K, che ha forma (2, 12) poiché ci sono 2 kernel e ogni kernel ha 12 elementi. Ecco come appare K:

Ora possiamo moltiplicare K con P che dà:

Infine, rimodelliamo il K P alla forma corretta, che secondo la formula è una “immagine” con forma (1, 5). Ciò significa che il risultato di questa convoluzione è un tensore con forma (2, 1, 5) poiché abbiamo impostato i canali di uscita a 2. Ecco come appare il risultato finale:

Che, come previsto, viene verificato se avessimo eseguito la convoluzione usando le funzioni integrate di PyTorch.