定義

変数 x の多項式は、an, an-1 , …, a2, a1, a0 が定数で、

形式で書くことができる関数である。 xの最高乗を含む項(すなわちanxn)を先行項と呼び、anを先行係数と呼ぶことにする。 多項式の次数は、先頭の項のxの累乗である。 すでに、0次、1次、2次の多項式は、それぞれ定数、1次、2次関数であることを見てきました。 次数3、4、5の多項式にも、3次関数、4次関数、5次関数という特別な名前がついています。 次数n > 5の多項式は、単にn次多項式と呼ばれる。 さまざまな多項式関数の名称を下表にまとめた。

定数関数

多項式の次数	関数の名前
0
1	一次関数
2	二次関数
3	3次関数
4	4次関数
5	5次関数
n（ここでnは> 5）	n次多項式

多項式の例としては、以下のようなものがある。

多項式の極限挙動

関数の極限挙動は、x → ±∞として関数がどうなるかを記述します。 多項式の次数と先行係数の符号が極限挙動を決定する。 特に、

これらの結果を下の表にまとめました。

この情報を使って、多項式のグラフを調べるだけで、その次数が奇数か偶数か、先頭の係数が正か負か判断することができるのです。

次の多項式のグラフは、上の表で説明した各動作の例証となるものです。

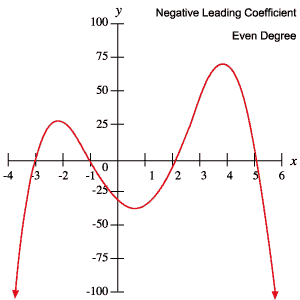
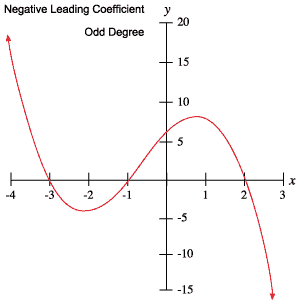
ルーツと転機

限界動作以上に多項式の次数はそれを教えてくれるものである。 具体的には、n次多項式は乗数を数えて最大n個の実根（x切片またはゼロ）を持つことができます。 例えば、4つの異なる根を持つ6次多項式を見ているとします。 4つの根のうち、2つが多重度2、残りの2つが多重度1であれば、6つの根をすべて占めたことになるので、他の根は存在しないことがわかる。

n次多項式は実根をn個持つ必要はなく、虚根を持つのでもっと少なくてもよいことに注意してください。 奇数次の多項式は、関数が片方で-∞、もう片方で+∞に近づくので、少なくとも1つの実根を持たなければならないことに注意してください。マイナスからプラスに変わる連続関数は、x-軸をその間のどこかで交差させなければなりません。 また、n次の多項式は最大でn – 1個の転換点を持つことができる。 転回点とは、下の図のように、関数が増加から減少、または減少から増加に転じる点である。 繰り返しになりますが、n次多項式はn – 1個の転回点を持つ必要はなく、もっと少ない場合もあります。

注意点

偶数と奇数関数、偶数と奇数次多項式の違いを認識することが重要です。 任意の関数 f(x) は、f(x) の領域内のすべての x に対して、

f(-x) = x,

ならば偶数、または f(x) の領域内のすべての x に対して、

f(-x) = -x,

なら奇数、上記のいずれも真の記述ではない場合は偶数と奇数のいずれかを示します。

k次の多項式p(x)はkが偶数なら偶数次、kが奇数なら奇数次という。 p(x)が偶数次であっても偶関数とは限らないことを覚えておいてください。 同様に、p(x)が奇数次を持つとしても、奇数関数であるとは限りません。

多項式の根を表すのにも偶数、奇数という言葉を使います。 具体的には、多項式 p(x) は (x – a)k が p(x) の因子である場合、多重度 k の根 x = a を持つ（すなわち x = a は k 回繰り返される根である）。 kが偶数ならx = aは偶数の多重度を持ち、kが奇数なら奇数の多重度を持つと言う。

定義域と範囲

すべての多項式はすべての実数からなる同じ定義域を持っています。 奇数次多項式の範囲もすべての実数で構成されます。 偶数次の多項式の範囲は少し複雑で、すべての偶数次の多項式の範囲を明示することはできません。 先頭の係数が正の場合は+ ∞まで、負の場合は- ∞までとなる。 つまり、先頭の係数が正の偶数次の多項式は、関数が到達するグローバルな最大値を示す範囲ymaxを持つことになる。 一般に、多項式の最大値や最小値を解析的に決定することはできない。

*****

次節では、多項式関数の根を求めるためのテクニックである多項式除算を学習します。