ベイジアンビリーフネットワークまたはベイズネットワークまたはビリーフネットワークは確率的グラフィカルモデル(PGM)で、確率変数間の条件依存性をDAG(Directed Acyclic Graph)によって表現するものである。
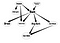
Today, I will try to explain the main aspects of Belief Network, especially for applications may be related to Social Network Analysis (SNA). また、この種のネットワークの実装例を紹介します。
ベイジアンネットワークは何に使うのか
ベイジアンネットワークは多くの分野で応用されています。 例えば、病気の診断、ウェブ検索の最適化、スパムフィルタリング、遺伝子制御ネットワークなどです。 そして、このリストは拡張することができます。 これらのネットワークの主な目的は、因果関係の構造を理解しようとすることです。 これを明確にするために、病気診断の問題を考えてみよう。 症状とその結果としての病気が与えられ、ビリーフネットワークを構築し、新しい患者が来たときに、それぞれの病気に対して確率を与えることで、どの病気が新しい患者を持っている可能性があるかを推論することができる。 同様に、このような因果関係は他の問題でも構築でき、推論技術を適用して興味深い結果を得ることができます。
簡単な確率の復習
続ける前に、記憶を呼び戻すために、条件付きの性質の定義を説明します。 条件付き確率とは、ある確率変数に他の確率変数が与えられたときの確率のことです。 これは、
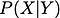
この二つの確率変数が従属であれば、
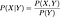
独立ならば、で示されるように、二つの確率変数は独立でなければならない。
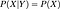
Belief Networksの数学的定義
確率は計算されます は、次の式
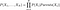
から理解できるように、信念ネットワークでは。 を計算するためには、ネットワークで示される条件付き確率が必要です。 しかし、さらに、もし結合分布がわかれば、面白い問いができるようになります。 例えば、最初の例では、「SEASON」が「WINTER」で「DOG BARK」が「TRUE」の場合、「RAIN」の確率を問うことにする。
Python によるビリーフネットワークの例
さて、理論はこのくらいにして、私のお気に入りのプログラミング言語 Python で実際の例を見てみましょう❤️ 先に、私が書いた Jupyter Notebook はこちらでご覧いただけます。
# create the nodes
season = BbnNode(Variable(0, 'season', ), )
atmos_pres = BbnNode(Variable(1, 'atmos_press', ), )
allergies = BbnNode(Variable(2, 'allergies', ), )
rain = BbnNode(Variable(3, 'rain', ), )
grass = BbnNode(Variable(4, 'grass', ), )
umbrellas = BbnNode(Variable(5, 'umbrellas', ), )
dog_bark = BbnNode(Variable(6, 'dog_bark', ), )
cat_mood = BbnNode(Variable(7, 'cat_mood', ), )
cat_hide = BbnNode(Variable(8, 'cat_hide', ), )bbn = Bbn() \
.add_node(season) \
.add_node(atmos_pres) \
.add_node(allergies) \
.add_node(rain) \
.add_node(grass) \
.add_node(umbrellas) \
.add_node(dog_bark) \
.add_node(cat_mood) \
.add_node(cat_hide) \
.add_edge(Edge(season, allergies, EdgeType.DIRECTED)) \
.add_edge(Edge(season, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(season, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(atmos_pres, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, grass, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, dog_bark, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, cat_mood, EdgeType.DIRECTED)) \
.add_edge(Edge(dog_bark, cat_hide, EdgeType.DIRECTED)) \
.add_edge(Edge(cat_mood, cat_hide, EdgeType.DIRECTED))
最初に、条件付き確率でノードについて説明しました。 単純化するために、いくつかの可能な状態を省略したことに気づくはずである。 例えば、季節の変数には「春」と「秋」という値がある。
with warnings.catch_warnings():
warnings.simplefilter('ignore')
graph = convert_for_drawing(bbn)
pos = nx.nx_agraph.graphviz_layout(graph, prog='neato')plt.figure(figsize=(20, 10))
plt.subplot(121)
labels = dict()
nx.draw(graph, pos=pos, with_labels=True, labels=labels)
plt.title('BBN DAG')
それでは、ネットワークが正しく構築されているかどうかを確認してみましょう。
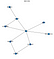
このように、最初に描いたグラフと同じになることがわかりますね。
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()join_tree.set_observation(ev)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
このコードスニペットは基本的に季節が1.0の確率で冬であるという証拠をネットワークに与えています。
0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.80000
3=sunny|0.20000
--------------------->
4|grass|grass,no_grass
4=grass|0.70000
4=no_grass|0.30000
--------------------->
1|atmos_press|high,low
1=high|0.50000
1=low|0.50000
--------------------->
5|umbrellas|on,off
5=on|0.95200
5=off|0.04800
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.66000
6=not_bark|0.34000
--------------------->
7|cat_mood|good,bad
7=good|0.23000
7=bad|0.77000
--------------------->
8|cat_hide|hide,show
8=hide|0.87150
8=show|0.12850
--------------------->
さらに犬が吠えていないなどの証拠を追加すると
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()ev2 = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('dog_bark')) \
.with_evidence('not_bark', 1.0) \
.build()join_tree.set_observation(ev)
join_tree.set_observation(ev2)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
以下の推論結果が得られます。 違いがわかりますか? 😆吠えに関する証拠を追加すると、たくさんの確率値が変化しました。 1292>
How to use Bayesian Networks in SNA?
Bayesian Networksは変数間の因果関係の構造を理解するのに非常に強力なツールです。 一度モデルを設計すれば、小さなデータセットであっても様々なことを教えてくれます。 このパートでは、SNAでベイジアンネットのメリットを得るにはどうしたらよいかということを考えます。 答えは一意ではありませんが、まずは深い考えから始めましょう。 SNAでは、ソーシャルネットワークの構造を理解しようとします。 また、ノードの重要性を理解しようとする。 しかし、その重要度測定の結果がどうなるかはわからない。 そこで、ベイジアンネットワークの出番となる。 例えば、ノードの重要度がDegree CentralityとLink Centralityで決まるとすると、次のようなネットワークになる。
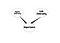
これは非常にナイーブなベイズネットワークと言える。 ノードの重要度を決定するだけでなく、さらに応用して、ある特定のタイプのノードを検索することができる。 例えば、社会的なネットワークで、リーダーとなりうる人が何人かいて、その人たちを探したい場合を考えてみよう。 次のグラフ
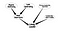
このもう少し複雑なネットワークは、リーダーになることに関連するノードの不確実性を判断するのに役立つだろう。 新しいリンクは、既存のものから推測することができる。 例えば、ソーシャルネットワークのグループメンバーシップから、メンバーシップの可能性が高いリンクを推論することができる。 つまり、既存のリンクを考慮することで、ユーザーとグループ間の新しいリンクをモデル化することができるのです。 以下のモデル図
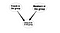
以上、SNAでベイズネットワークを適用できる基本例について説明しました。 このトピックはあまり研究されていませんが、さらに研究すると非常に役に立つと思います。
結論
ベイジアンネットワークで難しいのは設計です。 特にSNAの場合、Social Networkからベイジアンネットワークでマッピングを構築するのは科学というより芸術です😃しかし、一度芸術の仕事をし、モデルをうまく設計すれば、この便利なツールは多くのことを教えてくれます。 ベイジアンネットワークが様々な分野で応用されているのはご存知の通りです。 ほとんどのケースで非常にうまく機能しています。 したがって、私は、ソーシャルネットワークでも非常に深い推論ができると強く信じています。