振動や波の位相は、時間t = 0で指定した基準点からの変位のオフセットに対応する完全なサイクルの割合です。位相は周波数領域またはフーリエ変換領域の概念であり、そのように、単純な調和運動の観点から容易に理解することができます。 同じコンセプトが波動にも適用され、ある時間間隔での空間内の点、またはある瞬間の空間間隔を横切って見ることができる。 単純調和運動は、以下に示すように周期的に変化する変位です。png
式で表され、

ここでAは振動の振幅、fは周波数、tは時間、
- 一つは、
の初期変位はサイン関数と異なるが、同じ「位相」を持っているように見えることである。
- 時変角
やそのmodulo
値も一般には「位相」と呼ばれています。 1343>
時間的に変化する角度を初期条件と区別するために、瞬時位相という用語が使われる。 また、より一般的な関数に適用できる形式的な定義があり、t=0における関数の初期位相を明確に定義する。すなわち、サインとコサインは本質的に異なる初期位相を持っている。 特に明示されていない場合は、一般にcosineを推論する必要があります。 (位相器も参照)
位相シフト
位相シフトの図解です。 横軸は時間とともに大きくなる角度(位相)。

無限に長い正弦波では、


 |
 File:Sine waves same phase.svg File:Sine waves same phase.svg同相の波 逆相の波 左:平面波の実部が上から下へと移動している様子。 右は、同じ波が、例えば厚さの異なるガラスを通過することによって、中央部で位相がずれた後。 (右の図は、距離が遠くなるほど効果が大きくなる回折の影響を無視している) 同じ周波数で位相の異なる二つの振動子には位相差があり、振動子は互いに位相がずれているという。 このような発振器が互いにずれている量は、0°から360°までの度数、または0から2πまでのラジアン単位で表すことができる。 位相差が180度(πラジアン)であれば、2つの振動子は逆位相であると言われます。 相互作用する2つの波が逆位相の地点で出会うと、破壊的な干渉が起こります。 電磁波(光、RF)、音響(音)、その他のエネルギーの波が伝送媒体の中で重なり合うことはよくあることです。 このとき、位相差によって、互いに強め合うか、弱め合うかが決まります。 振動の周期内の位置を表すために、(角度の代わりに)時間が使われることがあります。
In-phase and Quadrature (I&Q) componentsIn-phaseという用語は、通信信号の文脈でも見られます。 _{sin \left(2}pi ft+{begin{matrix}{frac {}pi }{2}}end{matrix}} and: ここで
位相コヒーレンスコヒーレンスとは、波がその定義域の異なる領域で明確に定義された位相関係を示す性質のことです。 波動関数は複素数であり、その平方係数は物体を観測する確率と関連しているので、波動関数の複素数的性格は位相と関連している。 複素代数は量子力学の顕著な干渉効果を担っているので、粒子の位相はそれゆえ究極的にはその量子的挙動と関連しているのである 。 |

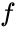 はキャリア周波数、
はキャリア周波数、

 and
and  は純粋キャリア波などの変調可能性を表します。
は純粋キャリア波などの変調可能性を表します。  この変調により、搬送波の元の
この変調により、搬送波の元の 成分が変化し、上記のように
成分が変化し、上記のように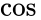 成分が生成されます。 このとき、元のキャリアと同位相の成分を同相成分と呼びます。 もう一方の成分は、常に90°(
成分が生成されます。 このとき、元のキャリアと同位相の成分を同相成分と呼びます。 もう一方の成分は、常に90°( radians)「位相がずれている」成分で、直交成分と呼ばれる。
radians)「位相がずれている」成分で、直交成分と呼ばれる。