Acta Cryst. (1992). A48, 727-732![]()
Final report of the International Union of Crystallography Ad-Hoc Committee on the nomenclature of symmetry*
By P. M. DE WOLFF (Chairman), Meermanstraat 126, 2614 AM Delft, The Netherlands,
Y. BILLIET, Ecole Nationale d’Ingénieurs, BPW 3038 Sfax, Tunesië、
J. D. H. DONNAY, Department of Geological Sciences, McGill University, 3450 University Street, Montreal, Canada H3A 2A7,
W. FISCHER, Institut für Mineralogie, Petrologie und Kristallographie der Phillips-Universität, Lahnberge, D-3550 Marburg (Lahn), Germany,
R.H. DONNAY, Department of Geological Sciences, McGill University, 3450 University Street, Canada H3A 2A7,W. B. GALIULIN, Institute of Crystallography, Academy of Sciences of Russia, Leninsky Prospekt 59, Moscow 117333, Russia,
A.M.A.(ロシア科学アカデミー結晶学研究所),
R. M. GLAZER, Clarendon Laboratory, University of Oxford, Parks Road, Oxford OX1 3PU England,
TH.M.GLAZER,クラレンドン・ラボラトリー, University of Oxford, Parks Road, Oxford OX1 3PU England. HAHN, Institut für Kristallographie, RWTH, Templergraben 55, D-5100 Aachen, Germany,
MARJORIE SENECHAL, Department of Mathematics, Smith College, Northampton, MA 01063, USA,
D.H.H., Institut für Kristallographie, RWTH, Templergraben 55, D-5100 Aachen, Germany,
Marticles, Inc. P. SHOEMAKER, Chemistry Department, Oregon State University, OR 97331, USA,
H. WONDRATSCHEK, Institut für Kristallographie, Universität Karlsruhe, Kaiserstrasse 12, D-7500 Karlsruhe 1, Germany,
A.P. SHOEMAKER, Universität Karlsruhe, Chemistry Department, USA,
H. J. C. WILSON (ex officio, IUCr Commission on International Tables), Crystallographic Data Centre, University Chemistry Laboratory, Lensfield Road, Cambridge CB2 1EW, England
AND S.C. C. (IUCr Commission on International Tables). ABRAHAMS (ex officio, IUCr Commission on Crystallographic Nomenclature), Department of Physics, Southern Oregon State College, 1250 Siskiyou Boulevard, Ashland, OR 97520-5047, USA
(Received 7 November 1991; accepted 9 March 1992)
* 任命は1987年8月10日にActa Cryst.に記載された基本規則に基づいて修正、1984年11月14日に就任、1992年8月10日に就任。 (1979), A35, 1072.
Abstract
最近認められた対称要素の再定義に照らして、新規または再定義の印刷記号が提案されている。 特に、eという文字は、これまで固有の記号を持たなかった滑空面、例えば「aかbのどちらか」と呼ばれる滑空面をカバーするものである。 5つの異なる空間群のヘルマン・マウグイン記号にeを使うことが推奨される。 平面に平行な方向に投影されたe平面については、現在の呼称のあいまいさを解消する図記号が提案された。 これまで特定の記号がなかった滑空面について、新たに定義された文字 k が提案されている。 International Tables for Crystallography (1989), Vol.A (Dordrecht: Kluwer Academic Publishers) の空間群記述で導入された対称操作の記号を、グライド反射操作のためだけに修正し、一般に使用することが推奨されます。
はじめに
「空間群における対称操作と対称要素に関する命名法の問題」を検討するために1980年に任命された特別委員会は、「結晶族、ブラベ格子型、算術クラスに対する命名法」(de Wolff et al…)という2つの報告書を発行しました。 1985)と「空間群および点群における対称要素の定義」(de Wolff et al.) 1989年の報告書で述べられているように、対称性のある演算については、概念が明確であるため、適切な記号を選択することが唯一の未解決の問題である。 3837>
Printed symbols for symmetry elements
1989 Report (de Wolff et al.) で示された対称要素の定義は、本報告書を通じて使用されます。 ここではそのエッセンスを繰り返す:
任意の対称操作について、その幾何学的要素(平面、点および/または線)が定義されている。 対称要素は、与えられた空間群の対称操作の1つの幾何学的要素と、この幾何学的要素を共有するその空間群のすべての対称操作の集合(「要素集合」と呼ぶ)の組み合わせである。
幾何学要素の明示的定義とそれに続く対称要素の説明およびそれらの記号は表1および2に示す(これらはグライド平面を除いて1989年の報告の表1および2と同じで、完全性のためにここで繰り返す、以下参照)。 各対称要素は2つの文字からなる記号で表される。 最初の文字は、すべての対称要素について大文字のEである。 これは、記号が対称要素に言及しており、例えば対称操作に言及していないことを示すのに役立つ。 文脈から明らかな場合は,Eを省略することができる。 点群および空間群における対称操作の幾何学的要素
Line b Line b
Line b Screw rotation = rotation about line b and translation ![]() parallel to b
parallel to b
None
対称要素が滑走面であることを示すだけなら、1989年報告書に記載された記号Egを滑走面に使用することができる。 一方,昔から適切な文字(a,b,c,n,d;ITA83参照)で示される特殊な種類の一つに属する場合は,その文字がEgのgに置き換わる。 点群と空間群における対称要素
Line b
translation along b, right-hand screw.このようなネジの場合、ネジの回転は、bを中心に回転します。 n = 2, 3, 4 or 6,
Line b and point P on b
* つまり、すべてのグライド反射は反射面が同じで、グライドベクトルはd.o.のもの(反射の場合は0とする)と格子並進ベクトルだけ異なる。![]() すなわち、同じ軸b、同じ角度と回転感覚、同じねじベクトル
すなわち、同じ軸b、同じ角度と回転感覚、同じねじベクトル![]() (回転はゼロ)までのすべての回転とねじ回転。
(回転はゼロ)までのすべての回転とねじ回転。![]() Egにおいて、特定の種類のグライドプレーンではgはa、b、c、n、d、eまたはkで置き換えられます、§2を参照して下さい。
Egにおいて、特定の種類のグライドプレーンではgはa、b、c、n、d、eまたはkで置き換えられます、§2を参照して下さい。
しかし、Ebのような記号の重要な新しい側面が指摘されるかもしれない。 ITA83によれば、bで平面を示すことは、単に、b軸に沿ったグライド成分b/2を持つ平面でのグライド反射が対称操作であることを意味するのみであった。 この定義は、図1に描かれた状況にも確かに当てはまる
\begin{figure} \Ίταμμα για για για για για για για \図1は、図2、3と同様に、特別委員会のメンバーであるW. Fischerが、あらゆるタイプの滑空機の目録として設計した同様の図のセットから採用したものである。 この図は、1989年の報告書が出るずっと前の1980年に委員会に提出されたものであるが、各図は、その報告書で定義された滑空機の「要素セット」(上記の要約を参照)を正確に示している。 グライドプレーンの場合、要素集合は、そのプレーンを共通の幾何学的要素とするすべてのグライドリフレクションで構成される。 その作用は、この平面への投影で示される。 任意の+記号の開始位置から、各-記号は集合の滑空反射のうちの1つから生じる。 これらすべては、結果として生じる+と-記号の2次元周期的パターンの初歩的なメッシュの中に示されている。
我々はしばしば、平面に平行なすべての並進によって形成されるネットNに言及することにする。 これらのベクトルは、+記号と任意の-記号を結ぶベクトルとは明確に区別され、それぞれが要素集合に属するグライド反射のグライドベクトルである
新しい側面は、ITA83定義により、いくつかの場合、b-グライド平面がa-グライド平面でもあることから生じる;図2を参照のこと。 これは明らかにネットNが直交中心である場合にのみ起こることで、その場合は中心移動の追加によってaグライドをbグライドに(またはその逆に)変更することができるからである。 これまでの慣習では、このようなグライド面を任意にaまたはbと呼んでいたため、これらの記号に不当な偏りが生じ、一意性を欠くことになった。 そこで、図2のようなケースは別の記号でカバーすることを提案する。
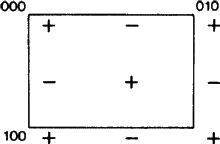
次に、この記号の範囲は、グライド平面がその軸に沿ってグライドベクトルを持ち、ネットNが直交中心であるという条件で、対角方向、すなわち、ただ一つの結晶軸に平行にグライド平面に拡張されるべきである。 このような面では、上記のa-bのランダムな選択のような曖昧さはなく、新しい記号の拡張範囲は、すべての既存の記号(すなわちa、b、c、nおよびd)のそれと一致している。 これらはそれぞれ、ネットNの1結晶軸と2結晶軸の両方を持つグライド面に用いられる(図3参照)
新シンボルにはeという文字が提案されている。 したがって、Eeは直交する中心ネットNと結晶軸に沿った少なくとも1つのグライドベクトルを持つグライドプレーンに適用されることになる。 すなわち、結晶の従来の軸に対するグライドベクトルの向きである。 結晶軸は対称性の方向に沿っており、一方グライド面は格子の鏡面に平行であるため、Nに少なくとも1つの結晶軸が存在することは驚くことではありません。
新しい記号eおよび古い記号a、b、c、d、nは、この新しい基準およびネットNのブラベタイプの観点から再定義されます。 ocタイプのネットNのみEe-グライドプレーンが可能です。 記号Enはブラベ型mpまたはopの網Nに、Edはoc型の網Nに適用される(ITA83の表1.3の脚注にあるように、「グライド面dは斜方晶F空間群、正方晶I空間群、立方晶IおよびF空間群にのみ存在する。 これらは常にグライドベクトルが交互に並ぶペアで発生する’。) しかし、Ea、Eb、Ec、Ee面とは対照的に、En、Ed面ではNの従来の軸に平行または垂直なグライドベクトルは存在しない。
以上の種類のグライド面の定義を表3の(i)、(ii)にまとめ、より明確に図3に示した。 特殊な種類の滑空機の印刷記号
記号は2つの基準で決定される。 一つの基準は、検討中の平面に平行な対称移動によって形成されるネットNのブラベ型(mp、op、tpまたはoc)である。 もう1つの基準は、このような軸に対するグライドベクトルの方向である。
* ITA83, § 9で定義されているとおりです。ただし、菱面体空間群については、ここでは六角軸のみを使用する。
残りのすべてのグライドプレーンは、以前は特定の記号がありませんでした。 それぞれ対角線方向(ネットNで従来の結晶軸が1本だけ)を持っています。 その要素セットに含まれるグライド反射のうち、その軸に沿ったグライドベクトルを持つものは存在しない。 しかし、1つのグライドベクトルは(対称性によって)それに垂直である。 新しい記号Ekは表3の(iii)行で簡単に定義され、図3の下のブロックに完全に示されている。 いくつかの例は§2に示す。
\begin{figure} \Ίταμμα για για για για για για για \図3は、Fischerによるすべてのタイプの滑空面の目録を、結晶軸をより強調した略図で(それでも完全ではあるが)示したものである。
いくつかの菱面体空間群では、斜めのEc、En、Ek面が、直交網の3重中心で記述できるmp型網Nとともに出現する。 図3、(2)、(9)、(14)にこれらのタイプのグライドプレーンに対するネットNの矩形3重メッシュを示す。 図(9)において、ネットNの単斜晶プリミティブメッシュを対角グライドベクトルで考えると、(8)や(10)のような他のN図との類似性が認められる。
対称要素の図記号
ITA83で定義されて使われている既存の図記号は、一つの例外を除いてアドホック委員会では適切と見なされている。 図面では投影方向が追加パラメータになるため、印刷記号の場合とは状況が大きく異なる。 以下、「垂直投影」「平行投影」の用語において、「垂直」「平行」はグライド面に対する投影方向の向きを指す。
Ee平面には、垂直投影の記号として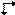 が存在する。 しかし、Ee-グライド面の平行投影のための既存の図記号は、印刷された記号と同じあいまいさに悩まされている。 それらは滑空ベクトルを投影方向に平行か垂直に表現するが、その選択は恣意的である。 そこで、Ee滑空面の平行投影を表す新しい記号、すなわち
が存在する。 しかし、Ee-グライド面の平行投影のための既存の図記号は、印刷された記号と同じあいまいさに悩まされている。 それらは滑空ベクトルを投影方向に平行か垂直に表現するが、その選択は恣意的である。 そこで、Ee滑空面の平行投影を表す新しい記号、すなわち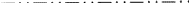
Ee滑空面の例、を提案する。
空間群Fmm2、Fmmm、![]() 、
、![]() 、
、![]() (42、69、202、225、226番)における2軸に平行なすべてのグライド面と、§3に挙げた5つの空間群のある面を挙げる。
(42、69、202、225、226番)における2軸に平行なすべてのグライド面と、§3に挙げた5つの空間群のある面を挙げる。
斜めEe面は空間群I4mm, I4cm, ![]() , I4/mmm, I4/mcm,
, I4/mmm, I4/mcm, ![]() and
and ![]() (Nos. 107, 108, 121, 139, 140, 217, 229)。
(Nos. 107, 108, 121, 139, 140, 217, 229)。
ITA83ではこれらのEe平面はすべて平行投影の点線か破線で任意に描かれている。 図4は空間群I4cm(No.108)の図であり、ITA83で示されたものと新しい記号を使用したものである
\begin{figure} \ʕ-̫͡-ʔ̫͡-ʔ \Ekは新しい印刷記号であるが、ITA83の図ではすべての滑空面EkはEa/b/c滑空面に使われるのと同じ慣例で満足に描かれてきた。 これらの場合と同様に、単一の特別なグライドベクトル(ネットNで結晶軸に垂直、表3参照)が存在する。 このベクトルが例えば投影面に平行な場合、Ek面は常に関連する慣習で規定された破線として描かれる。 したがって、Ek滑空面に対する新しい図記号は提案しない。
Ek面の例
このような面は、ITA83の図において、例えばP4bmのxxzや![]() (No. 100と113)のように1軸だけに平行に、破線として投影される平面として容易に見つけることができる。 特に、表3は、Ek面とEn面の区別と正確に一致している。 例えば、R3mとR3cの破線と点線(160番、161番)。
(No. 100と113)のように1軸だけに平行に、破線として投影される平面として容易に見つけることができる。 特に、表3は、Ek面とEn面の区別と正確に一致している。 例えば、R3mとR3cの破線と点線(160番、161番)。
ヘルマン・モーグイン空間群記号
空間群のヘルマン・モーグイン(HM)記号の格子文字の後に現れる文字は、もともと群の生成演算を表すもので、この記号の意味は次の通り。 例えば、bはHM記号の位置によって向きを変えた平面でのb-グライド反射であった。
実際には、定義が不明確ではあるが人気のある対称要素が操作に取って代わった。 こうして、bは現在の用語でいうところのグライド面、Ebとして見られるようになった。 このような再解釈は、演算がEe-グライド面に属する場合を除き、何の支障もない。 例えば、上記のb-グライド反射の場合、これが成り立つとすると、対応する方位にEeはあってもEb-グライド面は存在しないことになる。 この場合、bは非常に誤解を招きやすい文字となる。
そこで、このような誤解を招く文字aやbを、それらが出現する5つのHM記号すべてにおいてeに置き換えることを提案する:
| Space group No. | 39 | 41 | 64 | 67 | 68 |
| ITA83でのシンボルです。 | Abm2 | Aba2 | Cmca | Cmma | Ccca |
| New symbol: | Aem2 | Aea2 | Cmce | Cmme | Ccce.C |
提案された新しい記号のさらなる利点は、e – a や b とは異なり、中立であるため、軸の順列変更時に変化しないことです。
対称演算用の印刷記号
印刷記号の完全セットは W. Fischer & E. Koch (ITA83, §11.2) によって設計され、空間群記述の対称操作のセクションで広範囲に適用された。
要するに、各記号は最大で三つの部分から構成されている。 最初の部分は、操作の種類を記述する1文字(インデックスを付けることもある)である。 次の部分は関連するシフトまたは平行移動ベクトルの成分(常に括弧内)と操作の幾何学的要素の座標をこの順序で与える。
アドホック委員会は、このシステムを検討した後、グライド反射について2つの修正を導入したいと思います。
ルール(i)は、操作が属するグライド面の種類に関する情報を抑制しています。 その情報は無関係であったり、混乱を招くことが非常に多い。 a/b/c平面については、抑制によって重要な情報が破壊されることがありますが、下の例に示すように、ルール(ii)によって損失が回復します。
これらの変更を採用することによって、記号の統一性が、回転のものに関しても大幅に改善されます。 例えば、平面上の滑空反射 ![]() で、滑空ベクトル
で、滑空ベクトル ![]() , すなわち
, すなわち 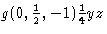 は単なる b-glide 反射と一線を画すものとなっています。 ITA83では後者は
は単なる b-glide 反射と一線を画すものとなっています。 ITA83では後者は![]() と表記されていましたが、規則(ii)によって
と表記されていましたが、規則(ii)によって![]() に変更されます。
に変更されます。
上記の規則は鏡面の要素集合に属する滑空反射に同様にあてはめられます。 したがって、そのような操作のシフト成分が (0, 1, 2) であれば、その記号は m(0, 1,2) ではなく g(0, 1, 2) で始まります。
International Tables for Crystallography (1983). A巻、TH.Edited。 HAHN, 特に§1.1, 1.3, 1.4, 7 and 11.です。 Dordrecht: Kluwer Academic Publishers.
International Tables for Crystallography (1989)。 Vol.A, 2nd, revised, ed., edited by TH. HAHN. Dordrecht: Kluwer Academic Publishers.
WOLFF, P.M. DE, BELOV, N.V., BERTAUT, E.F., BUERGER, M.J., DONNAY, J.D. H…, FISCHER, W., HAN, TH., KOPTSIK, V. A., MACKAY, A. L., WONDRATSCHEK, H., WILSON, A. J. C. & Abrahams, S. C. (1985). Acta Cryst. a41, 278-280.
wolff, p. m. de, billiet, y., donnay, j. d. h., fischer, w., galiulin, r. b., glazer, a. m., senechal, m., shoemaker, d. p., wondratschek, h., hahn, th., wilson, a. j. c. & abrahams, s. c. (1989).日本学術振興会特別研究員(DCAJ)。 Acta Cryst. A45, 494-499.
…ベクトル。 図3の(2)、(9)、(14)の3つの図の滑面記号c、n、kは、もちろん表3に従って割り当てられている。 アドホック委員会のメンバーの一人(Wondratschek教授)は、(9)の図の記号nは、n平面に関する伝統的な概念と矛盾する、と考えている。 彼は(9)図に特別な記号を割り当てることを提案した。 しかし、この提案はAd-hoc委員会では十分な支持を受けていない
。