分類は教師あり機械学習のアプローチであり、アルゴリズムは提供されたデータ入力から学習し、この学習を使用して新しい観測を分類します。

2値分類器は、2つのクラスまたは可能な結果のみを扱います（例：肯定的または否定的な感情、貸し手がローンを支払うかどうか、など）。 多クラス分類器は、各サンプルが1つだけのラベルに割り当てられると仮定しています。

機械学習における分類の最初の人気アルゴリズムの1つは、ベイズの定理（それを示唆するような観察の事前知識に基づいて現実世界で起こる事象の推論を行うことができる）に触発されて生まれた確率的分類法のナイーブベイズであった。 名前 (“Naive”) は、アルゴリズムが属性が条件付きで独立していると仮定していることに由来する。

このアルゴリズムは実装が簡単で、通常は分類作業を開始するための妥当な方法である。 より大きなデータセットに容易に拡張でき (他の多くの種類の分類器に使用される反復近似に対して線形時間がかかり、計算資源の点でより高価)、少量の学習データを必要とする。

しかし、ナイーブベイズは「ゼロ確率問題」として知られる問題に苦しむことがあり、特定の属性に対して条件付き確率がゼロであると、有効な予測を提供できなくなる。

P(c|x) は予測因子 (x, attributes) を与えられたクラス (c, target) の事後確立である。 P(c)はクラスの事前確率である。 P(x|c) はクラスが与えられたときの予測変数の確率である尤度であり、 P(x) は予測変数の事前確率である。

アルゴリズムの最初のステップは、与えられたクラス・ラベルの事前確率を計算することである。 そして、各属性、各クラスに対する尤度確率を求める。 その後、これらの値をベイズの式に入れ、&事後確率を計算し、入力がより高い確率のクラスに属していると仮定して、どのクラスがより高い確率を持つかを見る。 scikit-learnのライブラリには3種類のNaive Bayesモデルがあります。 (a) ガウス型 (特徴が鐘のような正規分布に従うと仮定)、(b) 多項式 (x 試行にわたって結果が観察された回数の観点から、離散カウントに使用)、および (c) ベルヌーイ (2 値特徴ベクトルに有用。一般的な使用例はテキスト分類) です。 属性のデータとそのクラスが与えられると、木はデータを分類するために使用できるルールのシーケンスを生成する。 アルゴリズムは、入力変数の最も重要な差別化要因に基づいて、サンプルを2つ以上の均質なセット（葉）に分割する。 差別化要因（予測因子）を選択するために、アルゴリズムはすべての特徴を考慮し、それらについてバイナリ分割を行います（カテゴリカル・データの場合はcatで分割、連続の場合はカットオフ閾値を選びます）。 そして、すべての葉でデータの分割に成功するまで（または最大深度に達するまで）、最小コスト（つまり、最高精度）のものを選び、再帰的に繰り返す。

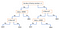
決定木は全般的に理解と視覚化が簡単で、データの事前準備があまり必要ない。 また、このメソッドは、数値データとカテゴリ データの両方を扱うことができます。 その一方で、複雑な木はうまく一般化できず (「オーバーフィット」)、データの小さな変化でまったく異なる木が生成される可能性があるため、決定木はやや不安定になることがあります。

決定木から派生した分類方法は Random Forest で、基本的にはデータセットのさまざまなサブサンプルに多数の決定木をフィットさせて平均を使用してモデルの予測的精度を改善しオーバーフィットを制御する「メタ推定」であります。 サブサンプルサイズは元の入力サンプルサイズと同じですが、サンプルは置換して抽出されます。

Random Forest はオーバーフィットに対して高い堅牢性（>データ中のノイズに対する堅牢性）、大きなデータセットでも効率の良い実行時間、を示している傾向にあります。 しかし、不均衡なデータセットにはより適しており、解釈はやや複雑で、より多くの計算資源を必要とします。

MLでもう一つ人気のある分類法はロジスティック回帰で、一つの裁判の可能な結果を記述する確率がロジスティック関数（名前に反して分類法）を使ってモデル化される：

ここでロジックの式はどのようであるかを示す。

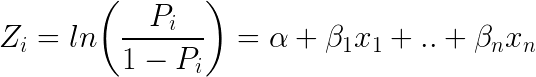
等式の両辺にe（指数）を取ると、次のようになる。

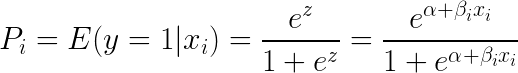
ロジスティック回帰は、1つの結果変数に対する複数の独立変数の影響を理解するのに最も有用である。 これは、2値分類に焦点を当てています（複数のクラスがある問題では、多項ロジスティック回帰や順序ロジスティック回帰など、ロジスティック回帰の拡張を使用します）。 ロジスティック回帰は、信用分析や反応/購買傾向などのユースケースで人気があります。

最後になりますが、kNN (「k Nearest Neighbors」の意) も分類問題によく使用されます。kNN は、すべての利用できるケースを保存し、類似性尺度 (たとえば、距離関数) に基づいて新しいケースを分類する、シンプルなアルゴリズムです。 ノンパラメトリックな手法として、すでに1970年代初頭から統計的推定やパターン認識の分野で使われている：