今回は、2次元畳み込みを行列の乗算として実装する方法を解説します。 CS231n Convolutional Neural Networks for Visual Recognition (Module 2)のノートに基づいて説明します。 読者はディープニューラルネットワークの文脈におけるコンボリューション演算の概念に慣れていることを前提としています。 そうでない場合は、このレポに畳み込みとは何かを説明したレポートと優れたアニメーションがあります。 本記事の計算を再現するコードは、こちらからダウンロードできます。

小例

シングルチャンネル 4 x 4 イメージ X があり、そのピクセル値は次のとおりだとします:

さらに次の性質を持つ 2D 畳み込みを定義すると仮定します。

つまり、このように行列Wと要素ごとに掛けられる2 x 2画像パッチが9つ存在することになるのです。

これらの画像パッチは4次元の列ベクトルとして表すことができ、以下のように連結して一つの4×9行列Pを形成することができる。

行列Pのi番目の列が実際には列ベクトルの形でi番目の画像パッチになることに注意してください。

畳み込み層の重みの行列Wは、次のように4次元の行ベクトル、Kに平坦化することができる。

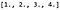
convolutionを行うために、まずKとPを行列掛けして9次元行ベクトルを得、これで計算を行う。

そしてK Pの結果を正しい形状、つまり3×3×1行列（チャンネル寸法は最後）にリシェイプするのです。 CS231nのノートによると、

つまり、コンボリューションの結果は、以下のようになります。

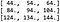
PyTorchの組み込み関数（詳細はこの記事の付属コード参照）で畳み込みを行うとチェックアウトすることができる。

大きな例

前のセクションの例では、単一のイメージと畳み込みの出力チャンネルが1であることを仮定しています。 これらの仮定を緩和すると、何が変わるでしょうか。

コンボリューションへの入力が、次のピクセル値を持つ 3 チャンネルの 4 x 4 イメージであると仮定しましょう。

畳み込みについては、出力フィルタが2である以外は前節と同じ性質とすることにします。 つまり、初期重み行列Wは（2、2、2、3）すなわち（出力フィルタ、カーネル高さ、カーネル幅、入力画像のチャンネル）の形状を持たなければならないことになります。 ここでは、Wが以下の値を持つように設定します。

各出力フィルタは独自のカーネルを持ち（これがこの例でカーネルが2つある理由）、各カーネルのチャンネルは3（入力画像は3チャンネルなので）であることに注意してください。

0 ゼロパディングとストライド 1 の 4 x 4 画像に 2 x 2 カーネルを畳み込んでいるので、画像パッチの数はまだ 9 です。 しかし、画像パッチの行列Pは異なります。 具体的には、Pのi番目の列は、画像パッチiに対応する第1、第2、第3チャンネルの値を（列ベクトルとして）連結したものとなります。 各画像パッチは3つのチャンネルを持ち，カーネルサイズを2×2に設定したため，各チャンネルは4つの要素を持つので，行は12となります． Pは次のようになります：

Wと同様に、各カーネルは行ベクトルにフラット化されて行ごとに連結され2×12行列Kとなることになります。 Kのi番目の行は、i番目のカーネルに対応する1、2、3番目のチャンネル値（行ベクトル形式）を連結したものです。 Kは次のようになります:

あとは行列積K Pを行って正しい形状に再整形するだけです。 正しい形状は3×3×2の行列です（チャンネル次元は最後）。 以下は乗算の結果です：

そして3×3×2行列に整形した結果がこちらです。

PyTorchの組み込み関数（詳細はこの記事の付属コード参照）で畳み込みを行った場合もチェックされます。

So What?

Why should we care about the 2D convolutions in terms of matrix multiplications? GPU 上での実行に適した効率的な実装を持つことに加え、このアプローチの知識により、深い畳み込みニューラルネットワークの動作について推論することが可能になります。 例えば、He et.al. (2015) は、2D 畳み込みを行列の乗算の観点から表現し、これにより、ランダム行列/ベクトルの特性を適用して、より良い重み初期化ルーチンを主張することができました。

Conclusion

この記事では、2 つの小さな例を見ながら、行列乗算を使って 2D 畳み込みを実行する方法について説明しました。 これで，任意の入力画像の次元や畳み込みの性質に一般化することができれば十分だと思います。 不明な点があればコメントで教えてください。

1D Convolution

この記事で説明した方法は、1D畳み込みにも一般化されます。

例えば、入力が次のような3チャンネルの12次元ベクトルだとします。

もし、1次元畳み込みを次のパラメータとする。

• カーネルサイズ：1×4
• 出力チャンネル：2
• ストライド：2
• パディング：2

。 0

• bias: 0

すると、畳み込み演算のパラメータWは、形状（2 , 3, 1, 4）のテンソルとなる。 Wが以下の値を持つように設定しよう：

畳み込み演算のパラメータに基づいて、「画像」パッチの行列P、は形状（12，5）（パッチが3チャンネルにわたって4つの要素を有するので各画像パッチが12次元ベクトルとなる5画像パッチ）を有し、以下のようになるであろう。

次に、Wを平らにしてKとすると、2カーネルあり各カーネルが12要素なので形状（2、12）であることがわかります。 これはKがどのようなものであるか:

ここでKにPを乗じることができ、これにより得られるのは以下の通りです。

最後に、K Pを正しい形に整形しますが、式によると形状（1、5）の「画像」となっています。 つまり、出力チャンネルを2にしたので、この畳み込みの結果は形状(2, 1, 5)のテンソルであることがわかります。

PyTorch組み込み関数を使って畳み込んだら予想通り確認できた