前節の方法はサンプルデータを記述し表示するのに便利ですが、統計の本当の力はサンプルを使って集団についての情報を与えるときに発揮されます。 この文脈では、母集団とは、例えば、我々のデータセットによって表される住宅市場におけるすべての一戸建て住宅の販売価格のような、関心のあるオブジェクトの全体のコレクションを指します。 この母集団についてもっと知って、どの家を買うかの判断材料にしたいが、我々が持っているデータは30の販売価格の無作為標本だけである。

それにもかかわらず、我々は「統計的思考」を採用して、標本データを分析することによって、関心のある母集団についての推論を導くことができる。 特に、モデル（現実の世界を数学的に抽象化したもの）という概念を用いて、サンプルデータに当てはめるのである。 このモデルがデータに適切にフィットする場合、つまり、データの変化の仕方を近似できる場合、そのモデルは母集団の挙動も近似できると仮定する。 このモデルは、パターンを特定し、変化を説明し、将来の値を予測するなど、母集団に関する意思決定の基礎となるものである。 もちろん、このプロセスは、サンプル・データが母集団を代表していると考えられる場合にのみ機能します。

サンプルがランダムに選択されていないことがわかっていても、モデル化できることがあります。 その場合、標本から母集団について正式に推論することはできないかもしれませんが、標本の基本的な構造をモデル化することは可能です。 例えば、コンビニエンス・サンプルは、統計的特性よりも利便性のために選ばれたサンプルです。 このような標本をモデル化する場合、どのような結果であっても、結論が標本と同様の対象に限定されることに注意して報告する必要があります。 もう一つの例は、標本が母集団全体を構成している場合である。 たとえば、アメリカ合衆国の 50 州すべてのデータをモデル化して、州間のパターンや系統的な関連性をよりよく理解することができます。

現実世界は非常に複雑な場合があるので（データ値が変化したり相互に作用したりする方法で）、モデルは問題を単純化して、それをよりよく理解できる（そして、より効果的に意思決定できる）ようにする点で役に立ちます。 そのため、モデルには、意思決定に簡単に使えるような単純さが求められる一方で、複雑な状況をうまく近似できるような柔軟さも求められます。 幸いなことに、この2つの基準を効果的にバランスさせた統計モデルが長年にわたって数多く開発されてきました。 そのようなモデルの 1 つは、後で考えるより複雑なモデルのための良い出発点となる正規分布です。

統計学の観点から、確率分布は確率変数がどのように変化するかを記述する理論モデルです。 我々の目的のために、確率変数は、例えば、我々の住宅市場におけるすべての一戸建ての家の販売価格など、母集団における関心のあるデータ値を表します。 データ値の母集団分布を表現する1つの方法は、セクション1.1で説明したように、ヒストグラムで表現することです。 ヒストグラムは、サンプルだけでなく、母集団全体を表示する点が異なります。 たとえば、以下は販売価格 1,000 件のシミュレーション集団のヒストグラムです。

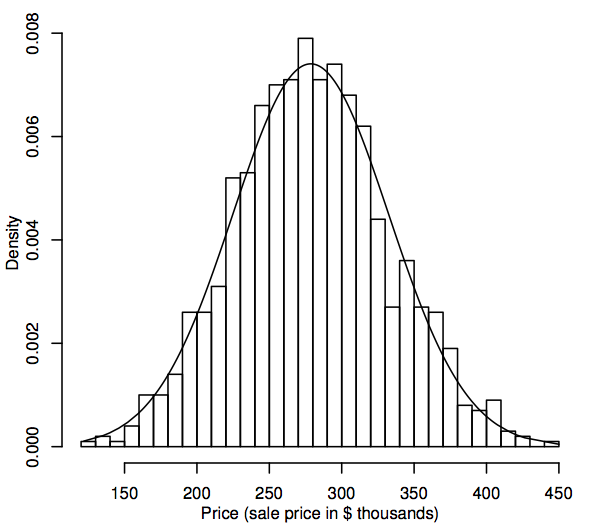
集団サイズが大きくなるにつれ、ヒストグラムのバーが細く、多くなり、一連のステップではなく、滑らかな曲線に似てくることが想像できます。 この滑らかな曲線は密度曲線と呼ばれ、母集団ヒストグラムの理論版と考えることができます。 密度曲線は、正規分布のような確率分布を視覚化する方法としても利用できます。 上のヒストグラムに正規密度曲線を重ねたものです。 シミュレーションされた人口ヒストグラムはこの曲線にかなり近く、このシミュレーションされた人口分布がかなり正規に近いことを示唆しています。

理論分布が、私たちの住宅価格の例のような人口について統計的推測を行うためにいかに役に立つかを見るために、正規分布をより詳しく見る必要があります。

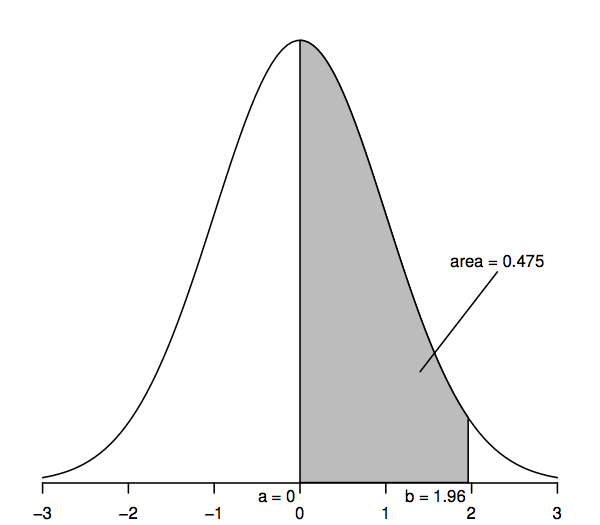
標準正規分布に従うランダム変数は、平均 0（曲線の最高点の下にある 0 について対称）、標準偏差 1（曲線の変曲点 – 曲線が最初に一方に曲がり、次に他方に曲がる場所 – +1 および -1） を持ちます。

統計的推論を可能にする正規密度曲線の重要な特徴は、曲線下の領域が確率を表していることです。 曲線下の面積全体は1であり、横軸のある点（例えばa）と別の点（例えばb）の間の曲線下の面積は、標準正規分布に従う確率変数がaとbの間にある確率を表しています。したがって、例えば上の図は、確率が0.475であることがわかります。

これらの面積や確率の値は、数表、電卓、表計算ソフト、統計ソフト、Webサイトなど、さまざまな方法で得ることができます。 後の計算のほとんどは “t 分布” と呼ばれる正規分布の一般化を使用しているため、以下ではいくつかの選択した値のみを印刷します。 また、上図のような網掛け部分ではなく、「尾部」（例． 特に1.96の右側の上尾領域は0.025で、これは0と1.96の間の領域が0.475（曲線下の領域全体が1、0の右側の領域が0.5なので）と言うのと同じ意味です。） 同様に、1.96の右と-1.96の左の面積を合計した2尾の面積は、0.025の2倍、つまり0.05です。

このことは、住宅価格の例などの集団について統計的に推論するのにどう役立つのでしょうか。 本質的な考え方は、サンプルデータに正規分布モデルを当てはめ、このモデルを使って対応する母集団について推論を行うことです。 例えば、正規分布の確率計算（上の図のように）を使って、その正規分布を使ってモデル化された母集団について確率的な記述をすることができます。 しかし、その前に、この推論を成功させるか失敗させるかを決定する、推論の順序の一面を考えてみましょう。 そのモデルは、標本値のパターンに十分近い近似値を提供し、そのモデルが母集団の値を適切に表していると確信できるでしょうか？ 密度曲線が非常に大きなサンプル サイズのヒストグラムと考えることができることを先に述べました。 したがって、母集団が正規分布モデルに従っているかどうかを評価する1つの方法は、サンプルデータからヒストグラムを作成し、それが「正規に見える」、つまり、ほぼ対称でベル型であるかどうかを視覚的に判断することです。 これはやや主観的な判断ですが、経験を積むと、明らかに非正規なヒストグラムと、それなりに正規なヒストグラムを見分けることが容易になることがわかります。 例えば、上のヒストグラムは明らかに正規の密度曲線のように見えますが、セクション1.1の30のサンプル販売価格のヒストグラムの正規性はあまり確かではありません。 この場合の合理的な結論は、このサンプルのヒストグラムは完全に対称的なベル型ではありませんが、対応する（仮説の）母集団のヒストグラムは十分に正常である可能性があるほど近いということです。

正規性を評価する別の方法は、住宅価格データについてここに示すように、正規確率プロットとしても知られる QQ プロット（分位数-分位数プロット）を構築することです：

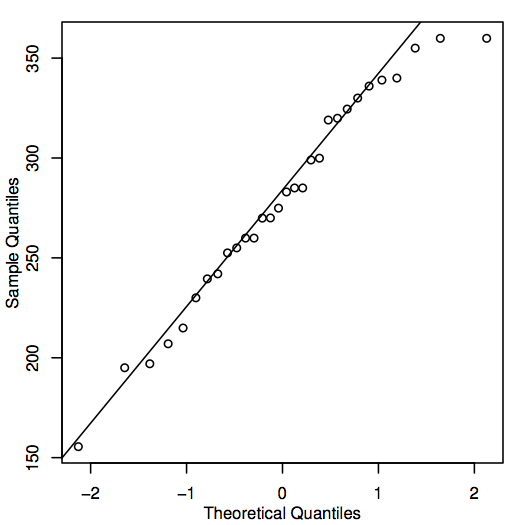
QQ-プロットのポイントが対角線の近くにある場合、対応する集団値は十分に正規であると考えられます。 もし点が一般に線から遠く離れているならば、正規性は疑問です。 これも主観的な判断であるが，経験を積むと容易に判断できるようになる。 この場合、かなり小さなサンプルサイズを考えると、ポイントはおそらく十分に直線に近く、母集団の値は正常であると結論づけるのは妥当でしょう。