La clasificación es un enfoque de aprendizaje automático supervisado, en el que el algoritmo aprende de la entrada de datos que se le proporciona – y luego utiliza este aprendizaje para clasificar nuevas observaciones.
En otras palabras, el conjunto de datos de entrenamiento se emplea para obtener mejores condiciones de contorno que se pueden utilizar para determinar cada clase objetivo; una vez que se determinan dichas condiciones de contorno, la siguiente tarea es predecir la clase objetivo.
Los clasificadores binarios trabajan con sólo dos clases o resultados posibles (ejemplo: sentimiento positivo o negativo; si el prestamista pagará el préstamo o no; etc), y los clasificadores multiclase trabajan con múltiples clases (ejemplo: a qué país pertenece una bandera, si una imagen es una manzana o un plátano o una naranja; etc). Los multiclase asumen que cada muestra es asignada a una y sólo una etiqueta.

Uno de los primeros algoritmos populares para la clasificación en el aprendizaje automático fue Naive Bayes, un clasificador probabilístico inspirado en el teorema de Bayes (que nos permite hacer una deducción razonada de los eventos que ocurren en el mundo real basándonos en el conocimiento previo de las observaciones que pueden implicarlo). El nombre («Naive») deriva del hecho de que el algoritmo asume que los atributos son condicionalmente independientes.
El algoritmo es sencillo de implementar y suele representar un método razonable para iniciar los esfuerzos de clasificación. Puede escalar fácilmente a conjuntos de datos más grandes (toma un tiempo lineal frente a la aproximación iterativa, como se utiliza para muchos otros tipos de clasificadores, que es más caro en términos de recursos de computación) y requiere una pequeña cantidad de datos de entrenamiento.
Sin embargo, Naive Bayes puede sufrir un problema conocido como ‘problema de probabilidad cero’, cuando la probabilidad condicional es cero para un atributo particular, no proporcionando una predicción válida. Una solución es aprovechar un procedimiento de suavización (por ejemplo, el método de Laplace).

P(c|x) es la probabilidad posterior de la clase (c, objetivo) dado el predictor (x, atributos). P(c) es la probabilidad a priori de la clase. P(x|c) es la probabilidad, que es la probabilidad del predictor dada la clase, y P(x) es la probabilidad previa del predictor.
El primer paso del algoritmo consiste en calcular la probabilidad previa para las etiquetas de clase dadas. Luego encontrar la probabilidad de verosimilitud con cada atributo, para cada clase. Posteriormente, poner estos valores en la fórmula de Bayes &calcular la probabilidad posterior, y luego ver qué clase tiene una mayor probablity, dado que la entrada pertenece a la clase de mayor probabilidad.
Es bastante sencillo de implementar Naive Bayes en Python aprovechando la biblioteca scikit-learn. En realidad hay tres tipos de modelo Naive Bayes bajo la biblioteca scikit-learn: (a) Tipo gaussiano (asume que las características siguen una distribución normal tipo campana), (b) Multinomial (utilizado para recuentos discretos, en términos de cantidad de veces que se observa un resultado a través de x ensayos), y (c] Bernoulli (útil para vectores de características binarias; el caso de uso popular es la clasificación de texto).
Otro mecanismo popular es el Árbol de Decisión. Dados unos datos de atributos junto con sus clases, el árbol produce una secuencia de reglas que pueden utilizarse para clasificar los datos. El algoritmo divide la muestra en dos o más conjuntos homogéneos (hojas) basados en los diferenciadores más significativos de sus variables de entrada. Para elegir un diferenciador (predictor), el algoritmo considera todas las características y realiza una división binaria sobre ellas (para datos categóricos, divide por catetos; para continuos, elige un umbral de corte). A continuación, elegirá el que tenga el menor coste (es decir, la mayor precisión), repitiendo recursivamente, hasta que divida con éxito los datos en todas las hojas (o alcance la máxima profundidad).
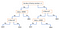
Los Árboles de Decisión son, en general, sencillos de entender y visualizar, y requieren poca preparación de datos. Este método también puede manejar datos numéricos y categóricos. Por otro lado, los árboles complejos no generalizan bien («sobreajuste»), y los árboles de decisión pueden ser algo inestables porque pequeñas variaciones en los datos pueden dar lugar a la generación de un árbol completamente diferente.
Un método de clasificación que se deriva de los árboles de decisión es el Bosque Aleatorio, esencialmente un «meta-estimador» que ajusta un número de árboles de decisión en varias sub-muestras de conjuntos de datos y utiliza el promedio para mejorar la precisión predictiva del modelo y controla el sobreajuste. El tamaño de la submuestra es el mismo que el tamaño de la muestra de entrada original, pero las muestras se extraen con reemplazo.
Los Bosques Aleatorios tienden a mostrar un mayor grado de robustez al sobreajuste (>robustez al ruido en los datos), con un tiempo de ejecución eficiente incluso en conjuntos de datos más grandes. Sin embargo, son más sensibles a los conjuntos de datos desequilibrados, siendo también un poco más complejos de interpretar y requiriendo más recursos computacionales.
Otro clasificador popular en ML es la Regresión Logística – donde las probabilidades que describen los posibles resultados de un solo ensayo se modelan utilizando una función logística (método de clasificación a pesar del nombre):

Aquí está el aspecto de la ecuación logística:
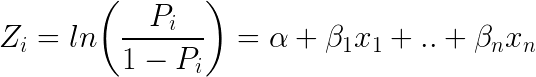
Tomando e (exponente) en ambos lados de la ecuación resulta:
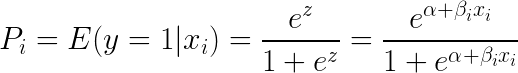
La regresión logística es más útil para comprender la influencia de varias variables independientes en una única variable de resultado. Se centra en la clasificación binaria (para problemas con múltiples clases, utilizamos extensiones de la regresión logística como la regresión logística multinomial y ordinal). La regresión logística es popular en casos de uso como el análisis de crédito y la propensión a responder/comprar.
Por último, pero no por ello menos importante, kNN (por «k Nearest Neighbors») también se utiliza a menudo para problemas de clasificación. kNN es un algoritmo sencillo que almacena todos los casos disponibles y clasifica los nuevos casos basándose en una medida de similitud (por ejemplo, funciones de distancia). Se ha utilizado en la estimación estadística y el reconocimiento de patrones ya a principios de la década de 1970 como técnica no paramétrica:


.