Weliswaar zijn de methoden uit de vorige paragraaf nuttig voor het beschrijven en weergeven van steekproefgegevens, maar de echte kracht van de statistiek komt aan het licht wanneer we steekproeven gebruiken om ons informatie te geven over populaties. In deze context is een populatie de volledige verzameling van interessante objecten, bijvoorbeeld de verkoopprijzen van alle eengezinswoningen op de woningmarkt die door onze dataset worden vertegenwoordigd. We zouden graag meer willen weten over deze populatie om ons te helpen een beslissing te nemen over welk huis te kopen, maar de enige gegevens die we hebben is een willekeurige steekproef van 30 verkoopprijzen.
Niettemin kunnen we “statistisch denken” gebruiken om conclusies te trekken over de populatie van belang door het analyseren van de steekproefgegevens. In het bijzonder gebruiken wij het begrip model – een wiskundige abstractie van de werkelijke wereld – dat wij aan de steekproefgegevens aanpassen. Als dit model redelijk bij de gegevens past, d.w.z. als het de manier waarop de gegevens variëren kan benaderen, dan nemen wij aan dat het ook het gedrag van de populatie kan benaderen. Het model vormt dan de basis voor het nemen van beslissingen over de populatie, bijvoorbeeld door patronen vast te stellen, variatie te verklaren en toekomstige waarden te voorspellen. Natuurlijk kan dit proces alleen werken als de steekproefgegevens als representatief voor de populatie kunnen worden beschouwd.
Soms, zelfs wanneer wij weten dat een steekproef niet willekeurig is gekozen, kunnen wij er toch een model van maken. In dat geval kunnen wij uit de steekproef misschien geen formele conclusies trekken over een populatie, maar kunnen wij toch de onderliggende structuur van de steekproef modelleren. Een voorbeeld hiervan is een gemakssteekproef – een steekproef die meer gemakshalve dan om zijn statistische eigenschappen wordt getrokken. Bij het modelleren van dergelijke steekproeven moeten de resultaten worden gerapporteerd met de waarschuwing dat de conclusies moeten worden beperkt tot objecten die lijken op die in de steekproef. Een ander soort voorbeeld is wanneer de steekproef de gehele populatie omvat. We zouden bijvoorbeeld gegevens voor alle 50 staten van de Verenigde Staten van Amerika kunnen modelleren om eventuele patronen of systematische associaties tussen de staten beter te begrijpen.
Omdat de echte wereld uiterst gecompliceerd kan zijn (in de manier waarop gegevenswaarden variëren of op elkaar inwerken), zijn modellen nuttig omdat zij problemen vereenvoudigen, zodat wij ze beter kunnen begrijpen (en dan doeltreffender beslissingen kunnen nemen). Enerzijds moeten de modellen dus zo eenvoudig zijn dat wij ze gemakkelijk kunnen gebruiken om beslissingen te nemen, maar anderzijds hebben wij modellen nodig die flexibel genoeg zijn om complexe situaties goed te benaderen. Gelukkig zijn er in de loop der jaren veel statistische modellen ontwikkeld die een goed evenwicht tussen deze twee criteria bieden. Eén zo’n model, dat een goed uitgangspunt vormt voor de meer gecompliceerde modellen die we later beschouwen, is de normale verdeling.
Vanuit een statistisch perspectief is een kansverdeling een theoretisch model dat beschrijft hoe een willekeurige variabele varieert. Voor onze doeleinden vertegenwoordigt een willekeurige variabele de gegevenswaarden die van belang zijn in de bevolking, bijvoorbeeld de verkoopprijzen van alle eengezinswoningen op onze woningmarkt. Eén manier om de populatieverdeling van gegevenswaarden weer te geven is in een histogram, zoals beschreven in paragraaf 1.1. Het verschil is nu dat het histogram de gehele populatie weergeeft in plaats van alleen de steekproef. Aangezien de populatie zoveel groter is dan de steekproef, kunnen de bins van het histogram (de opeenvolgende bereiken van de gegevens die de horizontale intervallen voor de staven vormen) veel kleiner zijn, bijvoorbeeld, het volgende toont een histogram voor een gesimuleerde populatie van 1.000 verkoopprijzen.
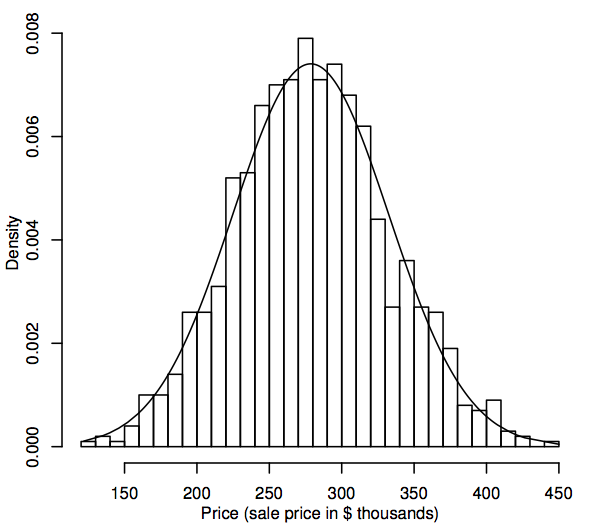
Naarmate de populatie groter wordt, kunnen we ons voorstellen dat de staven van het histogram dunner en talrijker worden, totdat het histogram meer op een vloeiende curve lijkt dan op een reeks stappen. Deze vloeiende curve wordt een dichtheidskromme genoemd en kan worden beschouwd als de theoretische versie van het populatiehistogram. Densiteitskrommen bieden ook een manier om waarschijnlijkheidsverdelingen zoals de normale verdeling te visualiseren. Een normale dichtheidscurve is gesuperponeerd op het histogram hierboven. Het gesimuleerde bevolkingshistogram volgt de curve vrij nauwkeurig, hetgeen suggereert dat deze gesimuleerde bevolkingsverdeling vrij dicht bij normaal ligt.
Om te zien hoe een theoretische verdeling nuttig kan blijken voor het maken van statistische gevolgtrekkingen over populaties zoals die in ons voorbeeld van de huizenprijzen, moeten we de normale verdeling nader bekijken. Om te beginnen bekijken we een bepaalde versie van de normale verdeling, de standaardnormaal, zoals voorgesteld door de volgende dichtheidskromme.
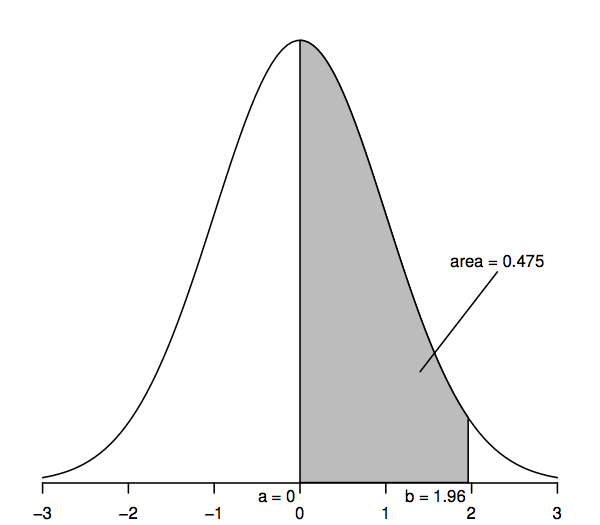
Randomvariabelen die een standaardnormale verdeling volgen, hebben een gemiddelde van 0 (zodat de kromme symmetrisch is rond 0, dat is onder het hoogste punt van de kromme) en een standaardafwijking van 1 (zodat de kromme een buigpunt heeft – waar de kromme eerst de ene kant op buigt en dan de andere kant – op +1 en -1). De normale dichtheidskromme wordt ook wel eens de “belkromme” genoemd, omdat zijn vorm op die van een bel lijkt.
Het belangrijkste kenmerk van de normale dichtheidskromme dat ons in staat stelt statistische gevolgtrekkingen te maken, is dat de gebieden onder de kromme waarschijnlijkheden voorstellen. Het gehele gebied onder de kromme is één, terwijl het gebied onder de kromme tussen een punt op de horizontale as (a, bijvoorbeeld) en een ander punt (b, bijvoorbeeld) de waarschijnlijkheid weergeeft dat een willekeurige variabele die een standaardnormale verdeling volgt, zich tussen a en b bevindt.475 dat een standaardnormale willekeurige variabele tussen a=0 en b=1,96 ligt, aangezien het gebied onder de curve tussen a=0 en b=1,96 0,475.
We kunnen de waarden voor deze gebieden of waarschijnlijkheden uit verschillende bronnen halen: tabellen met getallen, rekenmachines, spreadsheet- of statistische software, websites, enzovoort. Hieronder drukken wij slechts een paar geselecteerde waarden af omdat de meeste van de latere berekeningen een veralgemening van de normale verdeling gebruiken die de “t-verdeling” wordt genoemd. Ook zal het, in plaats van gebieden zoals die in de bovenstaande figuur gearceerd zijn, nuttiger worden om te kijken naar “staartgebieden” (bijv, rechts van punt b), en om consistent te zijn met latere tabellen met getallen, kunnen in de volgende tabel dergelijke staartgebieden worden berekend:
In het bijzonder is het gebied van de bovenstaart rechts van 1,96 0,025; dit komt erop neer dat het gebied tussen 0 en 1,96 0,475 is (aangezien het gehele gebied onder de kromme 1 is en het gebied rechts van 0 0 0,5 is). Evenzo is het tweestaartgebied, dat de som is van de gebieden rechts van 1,96 en links van -1,96, twee keer 0,025, of 0,05.
Hoe helpt dit alles ons om statistische gevolgtrekkingen te maken over populaties zoals die in ons voorbeeld van de huizenprijzen? De essentie is dat wij een normaal verdelingsmodel toepassen op onze steekproefgegevens en dit model vervolgens gebruiken om conclusies te trekken over de overeenkomstige populatie. We kunnen bijvoorbeeld kansberekeningen voor een normale verdeling gebruiken (zoals in de figuur hierboven) om waarschijnlijkheidsuitspraken te doen over een populatie die gemodelleerd is met die normale verdeling – we zullen in Paragraaf 1.3 precies laten zien hoe we dat moeten doen. Maar voor we dat doen, pauzeren we even om stil te staan bij een aspect van deze inferentiële volgorde dat het proces kan maken of breken. Geeft het model een voldoende goede benadering van het patroon van de steekproefwaarden om er zeker van te zijn dat het model de waarden van de populatie adequaat weergeeft? Hoe beter de benadering, hoe betrouwbaarder onze conclusies zullen zijn.
We hebben eerder gezien hoe een dichtheidscurve kan worden gezien als een histogram met een zeer grote steekproefgrootte. Een manier om te beoordelen of onze populatie een normaal verdelingsmodel volgt, is dus een histogram te construeren van onze steekproefgegevens en visueel te bepalen of het er “normaal” uitziet, dat wil zeggen, ongeveer symmetrisch en klokvormig. Dit is een enigszins subjectieve beslissing, maar met de ervaring zou je moeten merken dat het gemakkelijker wordt om duidelijk niet-normale histogrammen te onderscheiden van die welke redelijk normaal zijn. Terwijl bijvoorbeeld het bovenstaande histogram er duidelijk uitziet als een normale dichtheidskromme, is de normaliteit van het histogram van 30 verkoopprijzen uit een steekproef in punt 1.1 minder zeker. Een redelijke conclusie in dit geval zou zijn dat dit steekproefhistogram weliswaar niet volmaakt symmetrisch en klokvormig is, maar er toch dicht genoeg bij ligt dat het overeenkomstige (hypothetische) populatiehistogram wel eens normaal zou kunnen zijn.
Een alternatieve manier om de normaliteit te beoordelen is het construeren van een QQ-plot (quantile-quantile plot), ook bekend als een normale waarschijnlijkheidsplot, zoals hier getoond voor de huizenprijzen:
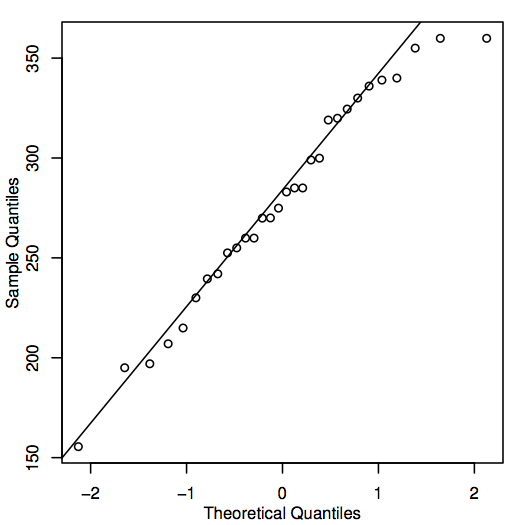
Als de punten in de QQ-plot dicht bij de diagonale lijn liggen, dan zouden de overeenkomstige populatiewaarden wel eens normaal kunnen zijn. Liggen de punten over het algemeen ver van de lijn, dan is er sprake van normaliteit. Ook dit is een enigszins subjectieve beslissing die met de ervaring gemakkelijker te nemen is. In dit geval liggen de punten, gezien de vrij kleine steekproefgrootte, waarschijnlijk dicht genoeg bij de lijn dat redelijkerwijs kan worden geconcludeerd dat de populatiewaarden normaal zouden kunnen zijn.
Er zijn ook een aantal kwantitatieve methoden om de normaliteit te beoordelen – zie paragraaf 6.3.