Introduction

Stel je dit eens voor – Je hebt de opdracht gekregen om de prijs van de volgende iPhone te voorspellen en je hebt historische gegevens gekregen. Dit omvat gegevens zoals kwartaalverkopen, maandelijkse uitgaven en een heleboel dingen die bij de balans van Apple horen. Als datawetenschapper, welk soort probleem zou je dit classificeren als? Tijdreeksmodellering, natuurlijk.

Van het voorspellen van de verkoop van een product tot het schatten van het elektriciteitsverbruik van huishoudens, tijdreeksvoorspelling is een van de kernvaardigheden die elke data scientist wordt geacht te kennen, zo niet te beheersen. Er is een overvloed aan verschillende technieken die je kunt gebruiken, en we zullen een van de meest effectieve, Auto ARIMA genaamd, in dit artikel behandelen.

We zullen eerst het concept van ARIMA begrijpen, wat ons zal leiden naar ons hoofdonderwerp – Auto ARIMA. Om onze concepten te consolideren, zullen we een dataset nemen en deze implementeren in zowel Python als R.

Tabel van de inhoud

1. Wat is een tijdreeks?
2. Methodes voor tijdreeksvoorspelling
3. Inleiding tot ARIMA
4. Stappen voor ARIMA-implementatie
5. Waarom hebben we AutoARIMA nodig?
6. Auto ARIMA implementatie (op luchtreizigers dataset)
7. Hoe selecteert auto ARIMA parameters?

Als u bekend bent met tijdreeksen en de bijbehorende technieken (zoals voortschrijdend gemiddelde, exponentiële afvlakking, en ARIMA), kunt u direct naar sectie 4 gaan. Beginners kunnen beginnen met de onderstaande paragraaf, die een korte inleiding geeft in tijdreeksen en verschillende voorspellingstechnieken.

Wat is een tijdreeks ?

Voordat we de technieken leren om met tijdreeksgegevens te werken, moeten we eerst begrijpen wat een tijdreeks eigenlijk is en hoe die verschilt van andere soorten gegevens. Hier volgt de formele definitie van tijdreeksen – Het is een reeks van gegevenspunten gemeten met consistente tijdsintervallen. Dit betekent eenvoudigweg dat bepaalde waarden worden geregistreerd met een constant interval dat elk uur, dagelijks, wekelijks, om de 10 dagen, enzovoort kan zijn. Wat tijdreeksen verschillend maakt, is dat elk gegevenspunt in de reeks afhankelijk is van de vorige gegevenspunten. Laten we het verschil duidelijker begrijpen aan de hand van een paar voorbeelden.

Voorbeeld 1:

Voorstel dat u een dataset hebt van mensen die een lening hebben genomen van een bepaald bedrijf (zoals weergegeven in de onderstaande tabel). Denk je dat elke rij zal worden gerelateerd aan de vorige rijen? Zeker niet! De door een persoon opgenomen lening zal gebaseerd zijn op zijn financiële voorwaarden en behoeften (er kunnen andere factoren zijn zoals de grootte van het gezin enz., maar om het eenvoudig te houden houden houden wij alleen rekening met het inkomen en het type lening) . Ook werden de gegevens niet op een bepaald tijdstip verzameld. Het hangt ervan af wanneer het bedrijf een verzoek om de lening heeft ontvangen.

Voorbeeld 2:

Laten we een ander voorbeeld nemen. Stel dat je een dataset hebt die het niveau van CO2 in de lucht per dag bevat (screenshot hieronder). Kun je dan voorspellen hoeveel CO2 er de volgende dag ongeveer zal zijn door naar de waarden van de afgelopen dagen te kijken? Wel, natuurlijk. Zoals u ziet, zijn de gegevens dagelijks geregistreerd, dat wil zeggen, het tijdsinterval is constant (24 uur).

U zult hier nu wel een intuïtie over hebben gekregen – het eerste geval is een eenvoudig regressieprobleem en het tweede is een tijdreeksprobleem. Hoewel de tijdreekspuzzel hier ook kan worden opgelost met lineaire regressie, maar dat is niet echt de beste aanpak omdat het de relatie van de waarden met alle relatieve vroegere waarden verwaarloost. Laten we nu eens kijken naar een aantal veelgebruikte technieken voor het oplossen van tijdreeksproblemen.

Methodes voor tijdreeksvoorspelling

Er zijn een aantal methoden voor tijdreeksvoorspelling en we zullen ze in dit gedeelte kort behandelen. De gedetailleerde uitleg en python codes voor alle hieronder genoemde technieken zijn in dit artikel te vinden: 7 technieken voor tijdreeksvoorspelling (met python codes).

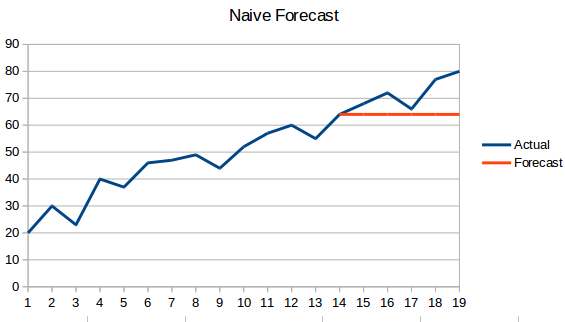
1. Naïeve benadering: Bij deze voorspellingstechniek wordt voorspeld dat de waarde van het nieuwe datapunt gelijk is aan het vorige datapunt. Het resultaat zou een vlakke lijn zijn, aangezien alle nieuwe waarden de vorige waarden overnemen.
2. Eenvoudig gemiddelde: De volgende waarde wordt genomen als het gemiddelde van alle vorige waarden. De voorspellingen zijn hier beter dan bij de “Naïeve benadering”, omdat deze niet in een vlakke lijn resulteert, maar hier worden alle vroegere waarden in aanmerking genomen, wat niet altijd nuttig kan zijn. Bijvoorbeeld, wanneer u gevraagd wordt de temperatuur van vandaag te voorspellen, zou u de temperatuur van de laatste 7 dagen in aanmerking nemen in plaats van de temperatuur van een maand geleden.
3. Voortschrijdend gemiddelde : Dit is een verbetering ten opzichte van de vorige techniek. In plaats van het gemiddelde van alle voorgaande punten te nemen, wordt het gemiddelde van ‘n’ voorgaande punten genomen als de voorspelde waarde.
4. Gewogen voortschrijdend gemiddelde : Een gewogen voortschrijdend gemiddelde is een voortschrijdend gemiddelde waarbij aan de afgelopen ‘n’ waarden verschillende gewichten worden gegeven.
5. Simple Exponential Smoothing: Bij deze techniek worden aan recentere waarnemingen grotere gewichten toegekend dan aan waarnemingen uit het verre verleden.
6. Holt’s Linear Trend Model: Deze methode houdt rekening met de trend van de dataset. Met trend bedoelen wij de stijgende of dalende aard van de reeks. Stel dat het aantal boekingen in een hotel elk jaar toeneemt, dan kunnen we zeggen dat het aantal boekingen een stijgende trend vertoont. De prognosefunctie in deze methode is een functie van niveau en trend.
7. Methode Holt Winters: Dit algoritme houdt rekening met zowel de trend als de seizoensgebondenheid van de reeks. Bijvoorbeeld – het aantal boekingen in een hotel is hoog in het weekend & laag op weekdagen, en neemt elk jaar toe; er bestaat een wekelijkse seizoensgebondenheid en een stijgende trend.
8. ARIMA: ARIMA is een zeer populaire techniek voor tijdreeksmodellering. Zij beschrijft de correlatie tussen datapunten en houdt rekening met het verschil tussen de waarden. Een verbetering ten opzichte van ARIMA is SARIMA (of seizoensgebonden ARIMA). We zullen ARIMA in de volgende sectie wat meer in detail bekijken.

Inleiding tot ARIMA

In deze sectie zullen we een korte inleiding tot ARIMA geven die nuttig zal zijn bij het begrijpen van Auto Arima. Een gedetailleerde uitleg van Arima, parameters (p,q,d), plots (ACF PACF) en implementatie is opgenomen in dit artikel: Complete tutorial to Time Series.

ARIMA is een zeer populaire statistische methode voor het voorspellen van tijdreeksen. ARIMA staat voor Auto-Regressieve Geïntegreerde Bewegende Gemiddelden. ARIMA-modellen werken op basis van de volgende veronderstellingen –

• De datareeks is stationair, wat betekent dat het gemiddelde en de variantie niet mogen variëren met de tijd. Een reeks kan stationair worden gemaakt door gebruik te maken van log-transformatie of door de reeks te differencen.
• De gegevens die als invoer worden verstrekt, moeten een univariate reeks zijn, aangezien arima de waarden uit het verleden gebruikt om de toekomstige waarden te voorspellen.

ARIMA heeft drie componenten – AR (autoregressieve term), I (differencing term) en MA (voortschrijdend gemiddelde term). Laat ons elk van deze componenten begrijpen –

• AR term verwijst naar de vroegere waarden die worden gebruikt voor het voorspellen van de volgende waarde. De AR-term wordt gedefinieerd door de parameter “p” in arima. De waarde van “p” wordt bepaald met behulp van de PACF-plot.
• MA term wordt gebruikt om het aantal in het verleden gemaakte prognosefouten te definiëren die worden gebruikt om de toekomstige waarden te voorspellen. De parameter “q” in arima vertegenwoordigt de MA-term. ACF plot wordt gebruikt om de juiste ‘q’-waarde te bepalen.
• Order of differencing specificeert het aantal malen dat de differencing-operatie wordt uitgevoerd op reeksen om deze stationair te maken. Testen zoals ADF en KPSS kunnen worden gebruikt om te bepalen of de reeks stationair is en helpen bij het bepalen van de d-waarde.

Stappen voor ARIMA-implementatie

De algemene stappen voor de implementatie van een ARIMA-model zijn –

1. Laad de gegevens: De eerste stap voor het bouwen van een model is natuurlijk het laden van de dataset
2. Voorbewerking: Afhankelijk van de dataset zullen de stappen van de voorbewerking worden bepaald. Dit omvat het maken van tijdstempels, het omzetten van het d-type van de datum/tijd-kolom, het univariaat maken van de reeks, enz.
3. Stationair maken van reeksen: Om aan de hypothese te voldoen, is het noodzakelijk de reeksen stationair te maken. Daartoe moet de stationariteit van de reeks worden gecontroleerd en moeten de vereiste transformaties worden uitgevoerd
4. Bepaal de d-waarde: Voor het stationair maken van de reeks wordt het aantal keren dat de verschiloperatie is uitgevoerd als d-waarde genomen
5. Maak ACF- en PACF-plots: Dit is de belangrijkste stap in de ARIMA implementatie. ACF PACF plots worden gebruikt om de inputparameters voor ons ARIMA-model te bepalen
6. Bepaal de p- en q-waarden: Lees de waarden van p en q uit de plots in de vorige stap
7. Fit ARIMA model: Pas het ARIMA-model met behulp van de verwerkte gegevens en de parameterwaarden die we uit de vorige stappen hebben berekend
8. Voorspel waarden op validatieset: Voorspel de toekomstige waarden
9. Bereken RMSE: Om de prestaties van het model te controleren, controleert u de RMSE-waarde met behulp van de voorspellingen en de werkelijke waarden op de validatieset

Waarom hebben we Auto ARIMA nodig?

Hoewel ARIMA een zeer krachtig model is voor het voorspellen van tijdreeksgegevens, zijn de gegevensvoorbereiding en parameterafstemmingsprocessen uiteindelijk zeer tijdrovend. Voordat u ARIMA implementeert, moet u de reeks stationair maken, en de waarden van p en q bepalen met behulp van de plots die we hierboven hebben besproken. Auto ARIMA maakt deze taak heel eenvoudig voor ons omdat het de stappen 3 tot 6 elimineert die we in de vorige sectie zagen. Hieronder staan de stappen die u moet volgen om auto ARIMA te implementeren:

1. Laad de gegevens: Deze stap zal hetzelfde zijn. Laad de gegevens in uw notebook
2. Voorbewerking van de gegevens: De invoer moet univariaat zijn, dus laat de andere kolommen weg
3. Fit Auto ARIMA: Fit het model op de univariate reeksen
4. Voorspel waarden op validatieset: Maak voorspellingen op de validatieset
5. Bereken RMSE: Controleer de prestaties van het model met behulp van de voorspelde waarden tegen de werkelijke waarden

We hebben de selectie van p- en q-kenmerken volledig omzeild, zoals u kunt zien. Wat een opluchting! In de volgende sectie zullen we auto ARIMA implementeren met behulp van een speelgoed dataset.

Implementatie in Python en R

We zullen gebruik maken van de International-Air-Passenger dataset. Deze dataset bevat het maandelijkse totaal van het aantal passagiers (in duizenden). Het heeft twee kolommen – maand en aantal passagiers. U kunt de dataset downloaden via deze link.

#load the datadata = pd.read_csv('international-airline-passengers.csv')#divide into train and validation settrain = datavalid = data#preprocessing (since arima takes univariate series as input)train.drop('Month',axis=1,inplace=True)valid.drop('Month',axis=1,inplace=True)#plotting the datatrain.plot()valid.plot()

#building the modelfrom pyramid.arima import auto_arimamodel = auto_arima(train, trace=True, error_action='ignore', suppress_warnings=True)model.fit(train)forecast = model.predict(n_periods=len(valid))forecast = pd.DataFrame(forecast,index = valid.index,columns=)#plot the predictions for validation setplt.plot(train, label='Train')plt.plot(valid, label='Valid')plt.plot(forecast, label='Prediction')plt.show()

#calculate rmsefrom math import sqrtfrom sklearn.metrics import mean_squared_errorrms = sqrt(mean_squared_error(valid,forecast))print(rms)

output -76.51355764316357

Hieronder staat de R-code voor hetzelfde probleem:

# loading packageslibrary(forecast)library(Metrics)# reading datadata = read.csv("international-airline-passengers.csv")# splitting data into train and valid setstrain = datavalid = data# removing "Month" columntrain$Month = NULL# training modelmodel = auto.arima(train)# model summarysummary(model)# forecastingforecast = predict(model,44)# evaluationrmse(valid$International.airline.passengers, forecast$pred)

Hoe selecteert Auto Arima de beste parameters

In de bovenstaande code hebben we gewoon de .fit() commando om het model te fitten zonder de combinatie van p, q, d te hoeven kiezen. Maar hoe heeft het model de beste combinatie van deze parameters bepaald? Auto ARIMA houdt rekening met de gegenereerde AIC- en BIC-waarden (zoals u in de code kunt zien) om de beste combinatie van parameters te bepalen. AIC-waarden (Akaike Information Criterion) en BIC-waarden (Bayesian Information Criterion) zijn schatters om modellen te vergelijken. Hoe lager deze waarden, hoe beter het model.

Kijk eens naar deze links als u geïnteresseerd bent in de wiskunde achter AIC en BIC.

End Notes and Further Reads

Ik heb auto ARIMA gevonden als de eenvoudigste techniek om tijdreeksvoorspellingen te doen. Een snelkoppeling kennen is goed, maar vertrouwd zijn met de wiskunde erachter is ook belangrijk. In dit artikel heb ik in vogelvlucht uitgelegd hoe ARIMA werkt, maar zorg ervoor dat u de links in het artikel doorneemt. Voor uw gemak zijn hier nogmaals de links:

• Een uitgebreide gids voor beginners voor het voorspellen van tijdreeksen in Python
• Volledige handleiding voor tijdreeksen in R
• 7 technieken voor het voorspellen van tijdreeksen (met python-codes)

Ik zou willen voorstellen om te oefenen wat we hier hebben geleerd op dit oefenprobleem: Time Series Practice Problem. U kunt ook onze training volgen die is gemaakt over hetzelfde oefenprobleem, Time series forecasting, om u een voorsprong te geven.