Een geïllustreerde uitleg van het uitvoeren van 2D Convoluties met behulp van Matrix Vermenigvuldigingen

In dit artikel zal ik uitleggen hoe 2D Convoluties worden geïmplementeerd als matrix vermenigvuldigingen. Deze uitleg is gebaseerd op de aantekeningen van de CS231n Convolutional Neural Networks for Visual Recognition (Module 2). Ik veronderstel dat de lezer vertrouwd is met het concept van een convolutie operatie in de context van een diep neuraal netwerk. Zo niet, dan heeft deze repo een verslag en uitstekende animaties die uitleggen wat convoluties zijn. De code om de berekeningen in dit artikel te reproduceren kan hier worden gedownload.

Klein voorbeeld

Voorstel dat we een eenkanaals 4 x 4 afbeelding hebben, X, en de pixelwaarden zijn als volgt:

Dit betekent dat er 9 beeldvakken van 2 x 2 zullen zijn die elementgewijs worden vermenigvuldigd met de matrix W, en wel als volgt:

Alle mogelijke 2 x 2 beeldflarden in X gegeven de parameters van de 2D-convolutie. Elke kleur vertegenwoordigt een uniek gebied

Deze beeldgebieden kunnen worden voorgesteld als 4-dimensionale kolomvectoren en aan elkaar worden gekoppeld tot een enkele 4 x 9 matrix, P, zoals hieronder:

Merk op dat de i-de kolom van matrix P in feite het i-de beeldflard in kolomvectorvorm is.

De matrix van gewichten voor de convolutielaag, W, kan worden afgevlakt tot een 4-dimensionale rijvector , K, zoals hieronder:

W als een afgevlakte rijvector K

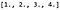
Om de convolutie uit te voeren, vermenigvuldigen we eerst K met P om een 9-dimensionale rijvector (1 x 9 matrix) te krijgen, die ons het volgende oplevert:

Het resultaat van K P

Dan hervormen we het resultaat van K P naar de juiste vorm, namelijk een 3 x 3 x 1 matrix (kanaaldimensie als laatste). De kanaaldimensie is 1 omdat we de uitvoerfilters op 1 hebben gezet. De hoogte en breedte is 3 omdat volgens de CS231noten:

formule om de hoogte te berekenen na het toepassen van een convolutiebewerking op een afbeelding. De formule om de breedte te berekenen is dezelfde (vervang gewoon de afbeeldingshoogte en de kernelhoogte door respectievelijk afbeeldingsbreedte en kernelbreedte

Dit betekent dat het resultaat van de convolutie is:

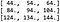
Eindresultaat van het uitvoeren van de convolutie met behulp van matrixvermenigvuldigingen

Wat klopt als we de convolutie uitvoeren met behulp van de ingebouwde functies van PyTorch (zie de begeleidende code van dit artikel voor details).

Groot voorbeeld

Het voorbeeld in de vorige sectie gaat uit van een enkel beeld en de uitgangskanalen van de convolutie is 1. Wat zou er veranderen als we deze aannames versoepelen?

Laten we aannemen dat onze invoer voor de convolutie een 4 x 4 afbeelding is met 3 kanalen met de volgende pixelwaarden:

Pixelwaarden in onze 4 x 4 x 3 invoerafbeelding

Wat onze convolutie betreft, stellen we in dat deze dezelfde eigenschappen heeft als in het vorige gedeelte, behalve dat de uitgangsfilters 2 is. Dit betekent dat de initiële gewichtenmatrix, W, de vorm (2, 2, 2, 3) moet hebben, d.w.z. (uitvoerfilters, kernelhoogte, kernelbreedte, kanalen van het invoerbeeld). Laten we W op de volgende waarden instellen:

Values for W given a 2 x 2 kernel, 2 uitvoerfilters en een invoerbeeld met 3 kanalen

Merk op dat elk uitvoerfilter zijn eigen kernel zal hebben (daarom hebben we in dit voorbeeld 2 kernels) en dat het kanaal van elke kernel 3 is (aangezien het invoerbeeld 3 kanalen heeft).

Omdat we nog steeds een 2 x 2 kernel convolueren op een 4 x 4 beeld met 0 zero-padding en stride 1, is het aantal beeldpatches nog steeds 9. De matrix van beeldvakken, P, zal echter anders zijn. Meer bepaald zal de i-de kolom van P de aaneenschakeling zijn van de waarden van het 1ste, 2de en 3de kanaal (als een kolomvector) die overeenstemmen met beeldveld i. P zal nu een 12 x 9 matrix zijn. De rijen zijn 12 omdat elk beeldfragment 3 kanalen heeft en elk kanaal heeft 4 elementen omdat we de kernelgrootte op 2 x 2 hebben gezet. Zo ziet P eruit:

Zoals voor W wordt elke kernel afgevlakt tot een rijvector en rijgewijs aan elkaar gekoppeld tot een 2 x 12 matrix, K. De i-de rij van K is de aaneenschakeling van de 1e, 2e en 3e kanaalwaarden (in rijvectorvorm) die overeenkomen met de i-de kernel. Zo ziet K eruit:

De 2 x 12 matrix van afgevlakte kernelwaarden in W, K

Nu hoeft alleen nog maar de matrixvermenigvuldiging K P te worden uitgevoerd en de vorm ervan te worden aangepast aan de juiste vorm. De juiste vorm is een matrix van 3 x 3 x 2 (kanaaldimensie laatste). Hier is het resultaat van de vermenigvuldiging:

Het resultaat van K P, een 2 x 9 matrix

En hier is het resultaat nadat het is omgevormd tot een 3 x 3 x 2 matrix:

Wat weer klopt als we de convolutie uitvoeren met behulp van de ingebouwde functies van PyTorch (zie de begeleidende code van dit artikel voor details).

Wat dan nog?

Waarom zouden we 2D-convoluties moeten uitdrukken in termen van matrixvermenigvuldigingen? Naast het hebben van een efficiënte implementatie die geschikt is om op een GPU te draaien, zal kennis van deze benadering ons in staat stellen te redeneren over het gedrag van een diep convolutioneel neuraal netwerk. Bijvoorbeeld, He et. al. (2015) 2D-convoluties uitgedrukt in termen van matrixvermenigvuldigingen, waardoor ze de eigenschappen van willekeurige matrices/vectoren konden toepassen om te pleiten voor een betere initialisatieroutine voor gewichten.

Conclusie

In dit artikel heb ik uitgelegd hoe 2D-convoluties kunnen worden uitgevoerd met behulp van matrixvermenigvuldigingen door twee kleine voorbeelden door te lopen. Ik hoop dat dit voldoende is voor u om te generaliseren naar willekeurige invoerafmetingen en convolutie-eigenschappen. Laat het me weten in de commentaren als er iets onduidelijk is.

1D Convolutie

De methode beschreven in dit artikel generaliseert ook naar 1D convoluties.

Voorstel bijvoorbeeld dat uw invoer een 12-dimensionale vector met 3 kanalen is, zoals dit:

Een invoer die een 12-D vector is met 3 kanalen

Als we onze 1D-convolutie instellen met de volgende parameters:

kernelgrootte: 1 x 4
uitvoerkanalen: 2
stride: 2
padding: 0
bias: 0

Dan zullen de parameters in de convolutiebewerking, W, een tensor zijn met vorm (2 , 3, 1, 4). Laten we W de volgende waarden geven:

Values for W. Merk op dat elke kernel een (3, 1, 4) tensor is

Op basis van de parameters van de convolutieoperatie zal de matrix van “beeld”-flarden P, een vorm (12, 5) hebben (5 beeldflarden waarbij elke beeldflard een 12-D vector is aangezien een patch 4 elementen over 3 kanalen heeft) en er als volgt uitzien:

Volgende, we vlakken W af om K te krijgen, die vorm (2, 12) heeft aangezien er 2 kernels zijn en elke kernel 12 elementen heeft. Zo ziet K eruit:

Waarden van K, een 2 x 12 matrix

Nu kunnen we K vermenigvuldigen met P, wat oplevert:

Het resultaat van K P, een 2 x 5 matrix

Tot slot hervormen we de K P tot de juiste vorm, die volgens de formule een “afbeelding” is met vorm (1, 5). Dit betekent dat het resultaat van deze convolutie een tensor is met de vorm (2, 1, 5), aangezien we de uitgangskanalen op 2 hebben ingesteld. Zo ziet het eindresultaat eruit:

Het resultaat van K P na het omvormen naar de juiste vorm

Wat zoals verwacht klopt als we de convolutie zouden uitvoeren met de ingebouwde functies van PyTorch.