Posted on

Fase (golven)

, Author

De fase van een oscillatie of golf is de fractie van een volledige cyclus die overeenkomt met een verschuiving in de verplaatsing ten opzichte van een gespecificeerd referentiepunt op het tijdstip t = 0. Fase is een begrip uit het frequentiedomein of het Fourier-transformatiedomein, en kan als zodanig gemakkelijk worden begrepen in termen van eenvoudige harmonische beweging. Hetzelfde concept is van toepassing op golfbewegingen, hetzij op een punt in de ruimte over een tijdsinterval, hetzij over een ruimte-interval op een tijdstip. Eenvoudige harmonische beweging is een verplaatsing die cyclisch varieert, zoals hieronder afgebeeld:

File:Eenvoudige harmonische beweging.png

en beschreven wordt door de formule:

{{Displaystyle x(t)=A:sin(2:ft+theta ),\,}

waarbij A de oscillatieamplitude is, f de frequentie, t de verstreken tijd, en {Displaystyle \theta } de fase van de oscillatie. De fase bepaalt of wordt bepaald door de beginverplaatsing op het tijdstip t = 0. Een beweging met frequentie f heeft periode {\displaystyle T={\frac {1}{f}}.

Twee mogelijke dubbelzinnigheden kunnen worden opgemerkt:

  • Een is dat de beginverplaatsing van {\displaystyle \cos(2} ft+theta )} anders is dan de sinusfunctie, maar toch lijken ze dezelfde “fase” te hebben.
  • De tijdsafhankelijke hoek {{\p+theta )} of de modulo {\p+theta )} waarde, wordt ook wel aangeduid als “fase”. Het is dan geen beginvoorwaarde, maar een continu veranderende toestand.

De term momentane fase wordt gebruikt om de tijdsafhankelijke hoek te onderscheiden van de beginvoorwaarde. Het heeft ook een formele definitie die van toepassing is op meer algemene functies en ondubbelzinnig de beginfase van een functie op t=0 definieert. D.w.z., sinus en cosinus hebben inherent verschillende beginfasen. Wanneer niet expliciet anders vermeld, moet cosinus in het algemeen worden afgeleid. (Zie ook fasor)

Faseverschuiving

File:Faseverschuiving.png

Illustratie van faseverschuiving. De horizontale as stelt een hoek (fase) voor die toeneemt met de tijd.

{\displaystyle \theta } wordt soms een faseverschuiving genoemd, omdat het een “verschuiving” vanaf fase nul voorstelt. Maar een verandering in {\displaystyle \theta } wordt ook wel een faseverschuiving genoemd.

Voor oneindig lange sinusoïden is een verandering in {\displaystyle \theta } hetzelfde als een verschuiving in de tijd, zoals een tijdvertraging. Als {\displaystyle x(t)} wordt vertraagd (verschoven in de tijd) met {\displaystyle {begin{matrix}{frac {1}{4}}\eind{matrix}} van zijn cyclus, dan wordt het:

{\displaystyle x(t-{\begin{matrix}{\frac {1}{4}}}}T)+theta )\,}

{{\displaystyle x(t-{\begin{matrix}{\frac {1}{4}}}})},} {\displaystyle =A\cdot \sin(2:\pi f(t-{\begin{matrix}{\frac {1}{4}}}}T)+theta )}
{{{>displaystyle =A\cdot \sin(2\pi ft-{\begin{matrix}{\frac {\pi }{2}}}end{matrix}+\theta )},

waarvan de “fase” nu {\displaystyle \theta -{\begin{matrix}{\frac {\pi }{2}}\eind{matrix}} is.}} Hij is verschoven met {\displaystyle {{\begin{matrix}{\frac {\pi }{2}}end{matrix}}.

Faseverschil

Bestand:Sinusgolven zelfde fase.svg

Golven in fase

File:Sinusgolven verschillende fase.svg

Golven buiten fase

File:Faseverschuiving illustratie.png

Links: het reële deel van een vlakke golf die van boven naar beneden beweegt. Rechts: dezelfde golf nadat een centraal gedeelte een faseverschuiving heeft ondergaan, bijvoorbeeld doordat hij door een glas is gegaan met een andere dikte dan de andere delen. (De afbeelding rechts houdt geen rekening met het effect van diffractie, waarvan het effect toeneemt over grote afstanden).

Twee oscillatoren die dezelfde frequentie en verschillende fasen hebben, hebben een faseverschil, en men zegt dat de oscillatoren met elkaar uit fase zijn. De mate waarin dergelijke oscillatoren met elkaar uit fase zijn, kan worden uitgedrukt in graden van 0° tot 360°, of in radialen van 0 tot 2π. Als het faseverschil 180 graden (π radialen) is, dan zijn de twee oscillatoren in antifase. Indien twee op elkaar inwerkende golven elkaar ontmoeten op een punt waar zij in antifase zijn, dan zal destructieve interferentie optreden. Het komt vaak voor dat golven van elektromagnetische (licht, RF), akoestische (geluid) of andere energie in hun transmissiemedium boven elkaar komen te liggen. Wanneer dat gebeurt, bepaalt het faseverschil of zij elkaar versterken of verzwakken. Volledige annulering is mogelijk voor golven met gelijke amplitudes.

Tijd wordt soms gebruikt (in plaats van hoek) om de positie binnen de cyclus van een oscillatie uit te drukken.

  • Een faseverschil is analoog aan twee atleten die met dezelfde snelheid en in dezelfde richting over een renbaan rennen, maar op verschillende plaatsen op de baan beginnen. Zij passeren een punt op verschillende momenten in de tijd. Maar het tijdsverschil (faseverschil) tussen hen is een constante – hetzelfde voor elke pas omdat zij met dezelfde snelheid en in dezelfde richting lopen. Als ze verschillende snelheden (verschillende frequenties) zouden hebben, zou het faseverschil slechts verschillende uitgangsposities weerspiegelen.
  • We meten de draaiing van de aarde in uren, in plaats van in radialen. En daarom zijn tijdzones een voorbeeld van faseverschillen.

In-fase en kwadratuur (I&Q) componenten

De term in-fase komt ook voor in de context van communicatiesignalen:

{\displaystyle A(t)\cdot \sin=I(t)\sin(2\p ft)+Q(t)\underbrace {{\cos(2\pi ft)}

en:

{Stijl A(t)\cdot \cos=I(t)\cdot \cos(2\pi ft)\underbrace {-Q(t)\cdot \sin(2\pi ft)} _{+Q(t)\cdot \cos \links(2\pi ft+{begin{matrix}{frac {\pi }{2}}\eind{matrix}}

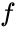
waar {displaystyle f,} een draaggolffrequentie voorstelt, en

{displaystyle I(t)\\\stackrel {\mathrm {def}} A(t) \cdot \cos,\,}{{Displaystyle Q(t)\ {\stackrel {\mathrm {def}} A(t)†cdot †sin,}

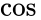
{\displaystyle A(t)† en {\displaystyle \phi (t)† staan voor mogelijke modulatie van een zuivere draaggolf, bijv: {displaystyle \sin(2)ft).} De modulatie verandert de oorspronkelijke {displaystyle \sin \,} component van de draaggolf, en creëert een (nieuwe) {displaystyle \cos \,} component, zoals hierboven getoond. De component die in fase is met de oorspronkelijke draaggolf wordt de in-fase component genoemd. De andere component, die altijd 90° (>{\displaystyle {\begin{matrix}{\frac {\pi }{2}}}eind{matrix}} radialen) “uit fase” is, wordt de kwadratuurcomponent genoemd.

Fasecoherentie

Coherentie is de eigenschap van een golf om goed gedefinieerde faseverhoudingen te vertonen in verschillende gebieden van zijn definiëringsdomein.

In de natuurkunde schrijft de kwantummechanica golven toe aan fysische objecten. De golffunctie is complex en aangezien de kwadraatmodulus ervan geassocieerd is met de waarschijnlijkheid van waarneming van het object, is het complexe karakter van de golffunctie geassocieerd met de fase. Aangezien de complexe algebra verantwoordelijk is voor het opvallende interferentie-effect van de kwantummechanica, is de fase van de deeltjes dus uiteindelijk gerelateerd aan hun kwantumgedrag.

Geef een antwoord

Het e-mailadres wordt niet gepubliceerd.