Bayesiaans Overtuigingsnetwerk of Bayesiaans Netwerk of Overtuigingsnetwerk is een Probabilistisch Grafisch Model (PGM) dat voorwaardelijke afhankelijkheden tussen willekeurige variabelen weergeeft door middel van een Directed Acyclic Graph (DAG).
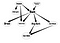
Vandaag zal ik proberen de belangrijkste aspecten van Belief Networks uit te leggen, vooral voor toepassingen die verband kunnen houden met Social Network Analysis (SNA). Bovendien zal ik een voorbeeld laten zien van de implementatie van dit soort netwerken.
Waarvoor gebruiken we Bayesiaanse Netwerken?
Bayesiaanse Netwerken worden op vele gebieden toegepast. Bijvoorbeeld, ziektediagnose, geoptimaliseerd zoeken op het web, spamfiltering, genregulerende netwerken, enz. En deze lijst kan nog worden uitgebreid. Het hoofddoel van deze netwerken is te proberen de structuur van causaliteitsrelaties te begrijpen. Laten we, om dit te verduidelijken, een probleem van ziektediagnose beschouwen. Met gegeven symptomen en de daaruit voortvloeiende ziekte, construeren we ons Belief Network en wanneer een nieuwe patiënt komt, kunnen we afleiden welke ziekte of ziekten de nieuwe patiënt kan hebben door waarschijnlijkheden te geven voor elke ziekte. Op dezelfde manier kunnen deze causaliteitsrelaties worden geconstrueerd voor andere problemen en kunnen inferentietechnieken worden toegepast om interessante resultaten te verkrijgen.
Snelle waarschijnlijkheidsbespreking
Voordat we verder gaan, wil ik u de definitie geven van voorwaardelijke eigenschap. Voorwaardelijke waarschijnlijkheid is de waarschijnlijkheid van een willekeurige variabele wanneer een andere willekeurige variabele gegeven is. Het wordt aangetoond door
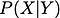
Als deze twee willekeurige variabelen afhankelijk zijn,
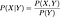
Als ze onafhankelijk zijn, dan
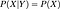
Mathematische definitie van overtuigingsnetwerken
De waarschijnlijkheden worden berekend in de overtuigingsnetwerken met de volgende formule
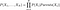
Zoals u uit de formule zou begrijpen, om de gezamenlijke verdeling te kunnen berekenen, moeten we voorwaardelijke waarschijnlijkheden hebben die door het netwerk worden aangegeven. Maar verder dat als we de gezamenlijke verdeling hebben, dan kunnen we interessante vragen gaan stellen. Bijvoorbeeld, in het eerste voorbeeld vragen we naar de kans op “RAIN” als “SEASON” “WINTER” is en “DOG BARK” “TRUE” is.
Python Voorbeeld van Belief Network
Zo, ik denk dat dit genoeg voor theorie en laten we eens zien wat echte voorbeeld met mijn huidige favoriete programmeertaal Python ❤️ Alvorens verder te gaan, kunt u de Jupyter Notebook die ik heb geschreven hier.
# create the nodes
season = BbnNode(Variable(0, 'season', ), )
atmos_pres = BbnNode(Variable(1, 'atmos_press', ), )
allergies = BbnNode(Variable(2, 'allergies', ), )
rain = BbnNode(Variable(3, 'rain', ), )
grass = BbnNode(Variable(4, 'grass', ), )
umbrellas = BbnNode(Variable(5, 'umbrellas', ), )
dog_bark = BbnNode(Variable(6, 'dog_bark', ), )
cat_mood = BbnNode(Variable(7, 'cat_mood', ), )
cat_hide = BbnNode(Variable(8, 'cat_hide', ), )bbn = Bbn() \
.add_node(season) \
.add_node(atmos_pres) \
.add_node(allergies) \
.add_node(rain) \
.add_node(grass) \
.add_node(umbrellas) \
.add_node(dog_bark) \
.add_node(cat_mood) \
.add_node(cat_hide) \
.add_edge(Edge(season, allergies, EdgeType.DIRECTED)) \
.add_edge(Edge(season, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(season, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(atmos_pres, rain, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, grass, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, umbrellas, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, dog_bark, EdgeType.DIRECTED)) \
.add_edge(Edge(rain, cat_mood, EdgeType.DIRECTED)) \
.add_edge(Edge(dog_bark, cat_hide, EdgeType.DIRECTED)) \
.add_edge(Edge(cat_mood, cat_hide, EdgeType.DIRECTED))
We eerst beschreven onze knooppunten met voorwaardelijke waarschijnlijkheden. U moet opmerken dat ik een aantal mogelijke toestand waarden overgeslagen voor de eenvoud. Bijvoorbeeld, seizoensvariabele nemen andere waarden “lente” en “herfst”. Het idee is dus hetzelfde.
Niet, laten we eens kijken of ons netwerk goed is opgebouwd of niet.
with warnings.catch_warnings():
warnings.simplefilter('ignore')
graph = convert_for_drawing(bbn)
pos = nx.nx_agraph.graphviz_layout(graph, prog='neato')plt.figure(figsize=(20, 10))
plt.subplot(121)
labels = dict()
nx.draw(graph, pos=pos, with_labels=True, labels=labels)
plt.title('BBN DAG')
Dit stukje code zou de volgende grafiek opleveren
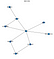
Zo, je ziet dat dit netwerk overeenkomt met mijn mooie tekening in het begin. Laten we nu wat inferentie doen op dit Belief Network.
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()join_tree.set_observation(ev)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
Dit stukje code geeft in feite bewijs aan het netwerk dat het seizoen winter is met een waarschijnlijkheid van 1,0. Volgens dit bewijs, wanneer we de gevolgtrekking doen, krijgen we de volgende resultaten.
0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.80000
3=sunny|0.20000
--------------------->
4|grass|grass,no_grass
4=grass|0.70000
4=no_grass|0.30000
--------------------->
1|atmos_press|high,low
1=high|0.50000
1=low|0.50000
--------------------->
5|umbrellas|on,off
5=on|0.95200
5=off|0.04800
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.66000
6=not_bark|0.34000
--------------------->
7|cat_mood|good,bad
7=good|0.23000
7=bad|0.77000
--------------------->
8|cat_hide|hide,show
8=hide|0.87150
8=show|0.12850
--------------------->
Wanneer we verder bewijs toevoegen, zoals de hond blaft niet
# convert the BBN to a join tree
join_tree = InferenceController.apply(bbn)# insert an observation evidence
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('season')) \
.with_evidence('winter', 1.0) \
.build()ev2 = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name('dog_bark')) \
.with_evidence('not_bark', 1.0) \
.build()join_tree.set_observation(ev)
join_tree.set_observation(ev2)# print the marginal probabilities
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print(node)
print(potential)
print('--------------------->')
We krijgen de volgende gevolgtrekking resultaten
0|season|winter,summer
0=winter|1.00000
0=summer|0.00000
--------------------->
2|allergies|allergic,non_alergic
2=allergic|0.70000
2=non_alergic|0.30000
--------------------->
3|rain|rainy,sunny
3=rainy|0.47059
3=sunny|0.52941
--------------------->
4|grass|grass,no_grass
4=grass|0.53529
4=no_grass|0.46471
--------------------->
1|atmos_press|high,low
1=high|0.39706
1=low|0.60294
--------------------->
5|umbrellas|on,off
5=on|0.88941
5=off|0.11059
--------------------->
6|dog_bark|bark,not_bark
6=bark|0.00000
6=not_bark|1.00000
--------------------->
7|cat_mood|good,bad
7=good|0.52647
7=bad|0.47353
--------------------->
8|cat_hide|hide,show
8=hide|0.83162
8=show|0.16838
--------------------->
Zien jullie het verschil? 😆 Veel waarschijnlijkheidswaarden veranderden wanneer we het bewijs toevoegden gerelateerd aan het blaffen. Het is beslist een dom voorbeeld, maar leuk om intuïtie te krijgen.
Hoe gebruik je Bayesiaanse netwerken in SNA ?
Bayesiaanse netwerken zijn zeer krachtige hulpmiddelen om de structuur van causaliteitsrelaties tussen variabelen te begrijpen. Als je eenmaal een model hebt ontworpen, kan het je zelfs met een kleine dataset verschillende dingen vertellen. De vraag in dit deel is hoe je Bayesiaanse Netwerken kunt gebruiken in SNA. Het antwoord is niet uniek, maar laten we beginnen met een diepgaand idee. In SNA proberen we de structuur van een sociaal netwerk te begrijpen. Bovendien proberen we het belang van de knooppunten te begrijpen. Maar we weten niet wat de resultaten zijn van onze metriek van belangrijkheid. Dit is het punt waar Bayesiaanse netwerken hun plaats innemen. Als u bijvoorbeeld denkt dat het belang van een knooppunt wordt bepaald door de Graad Centraliteit en de Verbindings Centraliteit, dan kunt u het volgende netwerk hebben.
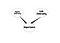
Dit is een zeer naïef Bayesiaans Netwerk. Naast het bepalen van het belang van de knooppunten, kan een verdere toepassing het zoeken naar een specifiek type van knooppunten zijn. Laten we een Sociaal Netwerk beschouwen waarin er enkele mensen zijn die potentiële leiders zijn en ik wil naar hen zoeken. Beschouw de volgende grafiek
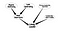
Dit iets gecompliceerdere netwerk zal ons helpen de onzekerheid te bepalen van de knooppunten die in verband kunnen worden gebracht met een leiderschap.
Een andere toepassing zou zijn het afleiden van de links. De nieuwe links kunnen worden afgeleid uit bestaande links. Bijvoorbeeld, uit het groepslidmaatschap in een sociaal netwerk kan een waarschijnlijke lidmaatschapsband worden afgeleid. Wat ik bedoelde is dat we een nieuwe link tussen gebruikers en groepen kunnen modelleren door bestaande links te beschouwen. Zie het volgende modeldiagram
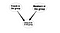
Dit zijn dus enkele basisvoorbeelden van hoe Bayesiaanse Netwerken kunnen worden toegepast in SNA. Dit onderwerp is niet erg goed bestudeerd, maar ik denk dat het erg nuttig kan zijn om verder te bestuderen.
Conclusie
Het lastige aan Bayesiaanse Netwerken is het ontwerpen. Vooral als je denkt aan SNA, is het construeren van mapping van Sociaal Netwerk met een Bayesiaans Netwerk meer kunst dan wetenschap 😃 Maar als je eenmaal de kunst af hebt en je model heel goed hebt ontworpen, kunnen deze handige tools je een hoop vertellen. Zoals we weten worden Bayesiaanse Netwerken op vele gebieden toegepast. In de meeste gevallen werkte het heel goed. Daarom ben ik ervan overtuigd dat we ook voor Sociale Netwerken zeer diepgaande conclusies kunnen maken.
Voor verder onderzoek met SNA en Bayesiaanse Netwerken, blijf a.u.b. op de hoogte 🚀