Vandaag gaan we de priemgetallen van 1 tot 100 leren. In de volgende werkbladen kunnen de kinderen van de Basisschool leren om priemgetallen te identificeren. Naast het leren van deze getallen, gaan we ook een aantal oefeningen doen met betrekking tot deze getallen, delers, etc…
Wat zijn priemgetallen?
Wat zijn priemgetallen? Priemgetallen zijn getallen die alleen gedeeld kunnen worden (zonder decimalen in het resultaat), door 1 en door zichzelf. Ze berekenen is onmogelijk, je moet ze leren. Kunnen priemgetallen berekend worden? Nee. Er bestaat geen wiskundige formule om te weten of een getal priem is of niet.
Priemgetallen zijn die getallen die alleen door 1 en door zichzelf kunnen worden gedeeld.
Maar we kunnen wel de eerste priemgetallen leren, in de hoeveelheden van 1 tot 100 bijvoorbeeld. Er zijn ook hulpmiddelen om uit te vinden welke getallen priem zijn, zoals de zeef van Eratosthenes, die we hieronder zullen zien.
Lijst van priemgetallen tussen 1 en 100:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 en 97
Om priemgetallen te herkennen is het van belang de tafels van vermenigvuldiging te kennen, zoals u kunt beginnen met het wegstrepen van de getallen die met 2, 3, 5, 7 vermenigvuldigd kunnen worden (we sluiten bijvoorbeeld 4 en 6 uit, omdat dat veelvouden zijn van het priemgetal 2). Deze methode om priemgetallen te verkrijgen wordt de zeef van Eratosthenes genoemd (zoals we later zullen zien). Hier is een werkblad voor kinderen om de priemgetallen te bestuderen.
Priemgetalentabel
We hebben de priemgetallen in de vorm van een tabel weergegeven, zodat kinderen ze altijd bij de hand kunnen hebben. Druk deze tabel af zodat kinderen de priemgetallen van 1 tot 100 op een gemakkelijke en visuele manier kunnen bestuderen en leren. Ze kunnen ook de priemgetaltabel raadplegen bij de oefeningen.
De tabel hieronder is ook zonder kleur te vinden, zodat de kinderen de getallen zelf kunnen inkleuren, of de zeef van Eratosthenes ermee kunnen doen.


Oefeningen met priemgetallen
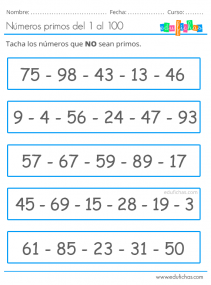
Na het leren van de priemgetallen met de bovenstaande tabel, volgen hier enkele oefeningen voor kinderen om de opgedane kennis in praktijk te brengen. De eerste tabel kan als oefening worden gebruikt, zodat de kinderen, dankzij hun kennis van de tafels van vermenigvuldiging, de getallen die geen priemgetal zijn, kunnen doorstrepen en de getallen die dat wel zijn, kunnen laten staan. Vergeet niet dat kennis van vermenigvuldigen en delen heel nuttig is voor kinderen om de oefeningen te kunnen maken.
 |
priemactiviteit | 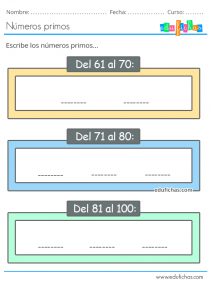 |
De eerste kaartjes helpen de kinderen om de priemgetallen van 1 tot 100 bij de hand te hebben, geordend per tiental. In elk van de vakjes is er ruimte om de overeenkomstige getallen te schrijven.
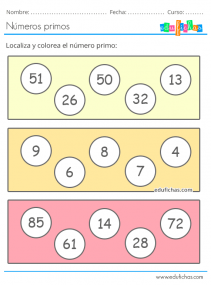
Daarna gaan we verder met deze oefeningen die ons vakjes met getallen voorschotelen. In elk van de dozen staan vijf getallen, waarvan er één een priemgetal is. De oefening is dat de kinderen het identificeren en inkleuren.
| priemgetallen oefening pdf |  |
 |
priemgetallen oefening pdf | priemgetallen oefeningen getallen |  |
Ons priemgetallen activiteitenboekje bevat ook vijf pagina’s waarin kinderen de delers moeten aanwijzen. Als u de afzonderlijke werkbladen wilt downloaden, kunt u ze hier vinden.
 |
 |
 |
Deze oefeningen zijn bedoeld voor kinderen van de basisschool. In deze sectie vindt u meer activiteiten voor de basisschool.
De zeef van Eratosthenes
De zeef van Eratosthenes is een fantastische oefening voor kinderen op de basisschool om de priemgetallen van 1 tot 100 te leren identificeren. Eratosthenes was een oude Griekse wiskundige die een manier heeft uitgevonden om de priemgetallen te verkrijgen. Hij noemde het de Eratosthenes zeef, en het bestaat uit het maken van een tabel met getallen van 1 tot 100 om uit te vinden welke priemgetallen zijn.
Dit is het sjabloon voor het maken van een Eratosthenes zeef en daarna zullen we uitleggen hoe we hieruit de priemgetallen kunnen halen. Degenen die niet priem zijn, strepen we door en degenen die priem zijn kleuren we in.


Je kunt onze tabel gebruiken (je vindt hem hierboven), met ongemarkeerde getallen van 1 tot 100, zodat kinderen de zeef van Eratosthenes kunnen toepassen als oefening om priemgetallen te leren. Bovendien zal het hen ook helpen om de tafels van vermenigvuldiging te herhalen, aangezien zij de veelvouden van de getallen, die overeenkomen met de resultaten van de tafels van vermenigvuldiging, zullen moeten doorstrepen.
Om de tafeloefening van Eratosthenes correct uit te voeren, kunnen de kinderen de volgende stappen volgen.
- Vind de veelvouden van 2 (en laat 2 ongemarkeerd, want het is een priemgetal).
- Doe hetzelfde met de veelvouden van 3 (en laat 3 ongemarkeerd, want het is ook een priemgetal).
- Het getal 4 is al doorgestreept (het is een veelvoud van 2), dus er hoeft niets te gebeuren.
- Vind de veelvouden van 5 (we laten het getal 5 ongemarkeerd omdat het priem is).
- We slaan 6 over omdat het zal worden doorgestreept, om dezelfde reden als 4.
- Vind de veelvouden van 7 en laat 7 ongemarkeerd omdat het priem is.
- We slaan 8 over (want het is een veelvoud van 2 en 4).
- Dan slaan we 9 over (want het is een veelvoud van 3).
- We slaan 10 over (want het is een veelvoud van 2 en 5).
- We zoeken naar de veelvouden van het getal 11.
En dan zouden we klaar zijn. Alle getallen die niet zijn doorgestreept zijn priemgetallen. Als u meer wilt weten over deze methode, bezoek dan dit item over Eratosthenes.
Prime numbers activity booklet
Download het priemgetallen activiteitenboekje in PDF. Dankzij dit bestand kunt u alle werkbladen op deze pagina in één bestand hebben en afdrukken. Het is de handigste manier als je alle oefeningen wilt doen. U vindt het bestand in deze link.


Download PDF
Prime numbers zijn nodig bij het berekenen van de grootste gemene deler en het kleinste gemene veelvoud. Daartoe voeren wij een priemfactorontleding uit, die bestaat uit het delen van de getallen met de priemgetallen als dividenden, tot wij 1 als resultaat krijgen. Om meer te leren over priemgetallen, raden wij u aan deze Yo Soy Tu Profe publicatie te lezen, waarin wordt uitgelegd hoe u kunt weten of een getal priem is of niet, evenals veel informatie om ze beter te begrijpen.
We hebben ook een korte video gemaakt waarin u dit notitieboekje kunt zien op ons YouTube-kanaal. Als u onze notebookvideo’s wilt bekijken, nodigen wij u uit u te abonneren op ons YouTube-kanaal.