(IUCr) Symbolen voor symmetrie-elementen

Acta Cryst. (1992). A48, 727-732

Eindrapport van het Ad-Hoc Comité van de Internationale Unie voor Kristallografie over de nomenclatuur van de symmetrie*

Door P. M. DE WOLFF (Voorzitter), Meermanstraat 126, 2614 AM Delft, Nederland,

Y. BILLIET, Ecole Nationale d’Ingénieurs, BPW 3038 Sfax, Tunesië,

J. D. H. DONNAY, Department of Geological Sciences, McGill University, 3450 University Street, Montreal, Canada H3A 2A7,

W. FISCHER, Institut für Mineralogie, Petrologie und Kristallographie der Phillips-Universität, Lahnberge, D-3550 Marburg (Lahn), Duitsland,

R. B. GALIULIN, Instituut voor Kristallografie, Academie van Wetenschappen van Rusland, Leninsky Prospekt 59, Moskou 117333, Rusland,

A. M. GLAZER, Clarendon Laboratory, University of Oxford, Parks Road, Oxford OX1 3PU England,

TH. HAHN, Institut für Kristallographie, RWTH, Templergraben 55, D-5100 Aachen, Duitsland,

MARJORIE SENECHAL, Department of Mathematics, Smith College, Northampton, MA 01063, USA,

D. P. SHOEMAKER, Departement Chemie, Oregon State University, OR 97331, USA,

H. WONDRATSCHEK, Institut für Kristallographie, Universität Karlsruhe, Kaiserstrasse 12, D-7500 Karlsruhe 1, Duitsland,

A. J. C. WILSON (ex officio, IUCr Commission on International Tables), Crystallographic Data Centre, University Chemistry Laboratory, Lensfield Road, Cambridge CB2 1EW, England

EN S. C. ABRAHAMS (ex officio, IUCr-commissie voor de kristallografische nomenclatuur), Department of Physics, Southern Oregon State College, 1250 Siskiyou Boulevard, Ashland, OR 97520-5047, USA

(Ontvangen 7 november 1991; aanvaard 9 maart 1992)

* Benoemd 14 november 1984, gewijzigd 10 augustus 1987 volgens de grondregels die zijn uiteengezet in Acta Cryst. (1979), A35, 1072. Eindrapport aanvaard 23 december 1991 door de Commissie voor Kristallografische Nomenclatuur van de IUCr en 9 maart 1992 door het Uitvoerend Comité.

Abstract

Nieuwe of opnieuw gedefinieerde druksymbolen worden voorgesteld in het licht van de onlangs aanvaarde herdefinitie van symmetrie-elementen . Met name de letter e omvat bepaalde glijvlakken die tot nu toe geen uniek symbool hadden, zoals die welke “ofwel a ofwel b” worden genoemd. Het gebruik van e in het Hermann-Mauguin-symbool van vijf verschillende ruimtegroepen wordt aanbevolen. Voor de vlakken van e, geprojecteerd in een richting evenwijdig aan het vlak, wordt een grafisch symbool voorgesteld dat de dubbelzinnigheid van hun huidige benaming wegneemt. De letter k wordt voorgesteld voor een nieuw gedefinieerde klasse van glijvlakken die tot nu toe zonder specifiek symbool waren. De symbolen voor symmetriebewerkingen die zijn geïntroduceerd in de ruimte-groep beschrijvingen van International Tables for Crystallography (1989), Vol. A (Dordrecht: Kluwer Academic Publishers) worden aanbevolen voor algemeen gebruik, met alleen wijzigingen voor glide reflectiebewerkingen.

Inleiding

Het ad-hoc comité dat in 1980 werd aangesteld om “nomenclatuurproblemen betreffende symmetriebewerkingen en symmetrie-elementen in ruimtegroepen” te bestuderen, heeft twee rapporten uitgebracht, getiteld Nomenclature for Crystal Families, Bravais-Lattice Types and Arithmetic Classes (de Wolff et al., 1985) en Definition of Symmetry Elements in Space Groups and Point Groups (de Wolff et al., 1989). Zoals opgemerkt in het rapport van 1989, is het enige onopgeloste probleem met betrekking tot symmetriebewerkingen dat van de keuze van geschikte symbolen, aangezien het concept duidelijk is. Een voorlopige notatie is overgenomen in de International Tables for Crystallography (1983, 1989), hierna aangeduid als ITA83.

Gedrukte symbolen voor symmetrie-elementen

De definitie van symmetrie-elementen zoals gegeven in het Rapport van 1989 (de Wolff et al.) zal in het gehele onderhavige Rapport worden gebruikt. We herhalen hier de essentie:

Voor elke gegeven symmetriebewerking wordt het bijbehorende geometrische element (vlak, punt en/of lijn) gedefinieerd. Een symmetrie-element is de combinatie van het meetkundige element van een van de symmetrie-operaties in een bepaalde ruimtegroep met de verzameling (`elementenset’ genoemd) van alle symmetrie-operaties in die ruimtegroep die dit meetkundige element gemeen hebben.

De expliciete definities van de meetkundige elementen en de beschrijvingen van de daaruit voortvloeiende symmetrie-elementen, alsmede hun symbolen, staan in de tabellen 1 en 2. (Deze zijn identiek aan de tabellen 1 en 2 in het rapport 1989, behalve voor de glijvlakken, en worden hier voor de volledigheid herhaald, zie hieronder). Elk symmetrie-element wordt weergegeven door een symbool bestaande uit twee tekens. Het eerste teken is een hoofdletter E voor alle symmetrie-elementen. Het dient om aan te geven dat het symbool verwijst naar een symmetrie-element en niet bijvoorbeeld naar een symmetrie-operatie. Als dit al duidelijk is uit de context, dan mag de E worden weggelaten, b.v. ‘een as 2’ in plaats van ‘een as E2’.

Tabel 1. Geometrische elementen van symmetriebewerkingen in puntgroepen en ruimtegroepen
Symmetriebewerking	Geometrisch element	Aanvullende parameters
Identity	Niet vereist	None
Translation	Niet vereist	Vector $\mathbf{t}$
Reflectie in vlak A	Vlak A	Neen
Glijreflectie =reflectie in vlak A en translatie $\mathbf{v}$ evenwijdig aan A	Vlak A	Glijvector $\mathbf{v}$
Rotatie om lijn b	Lijn b	Angle and sense of rotation
Wenteling = draaiing om lijn b en translatie $$\mathbf{u}$ evenwijdig aan b	Lijn b	Hoek en zin van rotatie schroefvector $\mathbf{u}$
Rotoinversie = rotatie om lijn b en inversie door punt P op b	Lijn b en punt P op b	Angle (niet gelijk aan $\pi$ ) en rotatiezin
Inversie door punt P	Punt P	None

Het in het rapport van 1989 vermelde symbool Eg kan voor glijvlakken worden gebruikt als men alleen maar wil aantonen dat het symmetrie-element een glijvlak is. Behoort het daarentegen tot een van de bijzondere soorten die reeds lang met een passende letter worden aangeduid (a, b, c, n of d; vgl. ITA83), dan vervangt die letter g in Eg.

Tabel 2. Symmetrie-elementen in puntgroepen en ruimtegroepen
Naam van symmetrie-element	Symbool	Geometrisch element	Definiërende bewerking (d.o.)	Operaties in elementenverzameling
Spiegelvlak	Em	Vlak A	Reflectie in A	D.o. en zijn coplanaire equivalenten*
Glijvlak	Eg	Vlak A	Glijspiegeling in A, 2v (niet v) een tralietranslatie	D.o. en zijn coplanaire equivalenten*
Rotatie-as	En	Lijn b	Rotatie om b, hoek $2\pi/n$ , n = 2, 3, 4 of 6	1e,$(n – 1)-machten van d.o. en hun coaxiale equivalenten
Schroefas	Enj	Lijn b	Schroefrotatie om b, hoek $2\pi/n$ , u =j/n maal kortste raster translatie langs b, rechterschroef; n = 2, 3, 4 of 6,	1e,$(n – 1)¤1450>,(n – 1)¤ machten van d.o. en hun coaxiale equivalenten
Rotoinversie-as		Lijn b en punt P op b	Rotoinversie: rotatie om b, hoek $2\pi/n$ , en inversie door P; n = 3, 4 of 6	D.o. en zijn inverse
Center		Punt P	Inversie door P	D.o. alleen

* Dat wil zeggen, alle glijreflecties met hetzelfde reflectievlak, waarbij de glijvectoren verschillen van die van het d.o. (dat voor een reflectie op nul wordt gesteld) door een tralievertalingsvector.
Dat wil zeggen alle rotaties en schroefrotaties met dezelfde as b, dezelfde hoek en zin van de rotatie en dezelfde schroefvector(nul voor een rotatie) tot en met een tralietranslatievector.
In Eg wordt g vervangen door a, b, c, n, d, e of k voor specifieke soorten glijvlakken, cf. §2.

Er kan echter worden gewezen op een belangrijk nieuw aspect van symbolen als Eb. Volgens ITA83 betekende het aanduiden van een vlak met b slechts dat een glijweerspiegeling in het vlak met een glijcomponent b/2 langs de b-as een symmetrieoperatie is. Deze definitie is zeker van toepassing op de situatie afgebeeld in Fig. 1.

Fig. 1. (Naar W. Fischer.) De elementenverzameling van een Eb-glijvlak, weergegeven als een verzameling punten boven (+) en onder (-) het vlak dat ontstaat door glijreflecties in het vlak, bijvoorbeeld beginnend bij het + teken linksboven. De netto N van vertalingen evenwijdig aan het vlak (+

+ vectoren) wordt aangegeven door een maas, die in dit geval toevallig rechthoekig is. Beide paren randen zijn evenwijdig aan de kristalassen. Er is een glijreflectie met zijn glijvector (+ $\cdots$ -) langs de b-as.

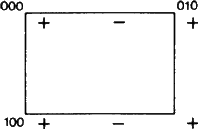
$\begin{figure} \includegraphics {fig1.ps}$

Figuur 1 is, net als fig. 2 en 3, ontleend aan een reeks soortgelijke figuren die door ad-hoccomitélid W. Fischer is ontworpen als een inventaris van alle typen glijvlakken. Hoewel de set aan het comité werd gepresenteerd in 1980, lang voordat het rapport van 1989 uitkwam, toont elk van de figuren precies de “elementenverzameling” van het glijvlak zoals gedefinieerd in dat rapport (cf. de bovenstaande samenvatting). Voor een glijvlak bestaat de verzameling van elementen uit alle glijreflecties die het vlak als gemeenschappelijk meetkundig element hebben. Hun werking wordt weergegeven in projectie op dit vlak. Vanuit de startpositie van een willekeurig + teken, resulteert elk – teken uit een van de glijreflecties van de verzameling. Al deze worden getoond binnen een elementaire maas van het resulterende tweedimensionale periodieke patroon van + en – tekens.

We zullen vaak verwijzen naar het net N gevormd door alle vertalingen evenwijdig aan het vlak; dit net is gemakkelijk zichtbaar te maken door alleen naar + tekens te kijken. Deze vectoren moeten scherp onderscheiden worden van de vectoren die een + teken met een willekeurig – teken verbinden en die elk de glijvector zijn van een glijreflectie die tot de elementenverzameling behoort.

Het nieuwe aspect ontstaat omdat in sommige gevallen, volgens de ITA83-definitie, het b-glijvlak ook een a-glijvlak is; zie Fig. 2. Het is duidelijk dat dit alleen gebeurt als het net N orthogonaal gecentreerd is, want dan kan het a-glijvlak worden veranderd in een b-glijvlak (en omgekeerd) door een centrering translatie toe te voegen. De praktijk tot nu toe was om zo’n glijvlak willekeurig ofwel a ofwel b te noemen, waardoor een ongerechtvaardigd vooroordeel en een gebrek aan uniciteit in deze symbolen ontstond. Daarom stellen wij voor om voor het geval van fig. 2 een afzonderlijk symbool te gebruiken.

Fig. 2. (Naar W. Fischer.) De elementenverzameling van een Ee-glijvlak. Cf. onderschrift van Fig. 1. Merk op dat het net N hier orthogonaal gecentreerd is.

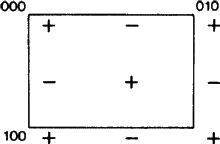
$\begin{figure} \includegraphics {fig2.ps}$

De werkingssfeer van dit symbool moet dan worden uitgebreid tot glijvlakken in een diagonale oriëntatie, dat wil zeggen, evenwijdig aan slechts één kristalas, mits het glijvlak een glijvector langs die as heeft en het net N orthogonaal gecentreerd is. Voor dergelijke vlakken is er niet de dubbelzinnigheid van de bovengenoemde a-b willekeurige keuze, maar de uitgebreide reikwijdte van het nieuwe symbool komt overeen met die van alle bestaande symbolen (namelijk a, b, c, n en d). Elk van deze wordt gebruikt voor een glijvlak met zowel één als twee kristalassen in het net N, cf. Fig. 3.

De letter e wordt voorgesteld voor het nieuwe symbool. Ee zal dus van toepassing zijn op glijvlakken met orthogonale gecentreerde netten N en ten minste één glijvector langs een kristalas. Er is dus een nieuw criterium nodig: namelijk de oriëntatie van de glijvectoren ten opzichte van de conventionele assen van het kristal. Aangezien deze laatste langs symmetrie-richtingen lopen, terwijl elk glijvlak evenwijdig is aan een spiegelvlak van het rooster, is het niet verwonderlijk dat er altijd minstens één conventionele kristal-as is in N. Als er slechts één zo’n as is, dan is er loodrecht daarop altijd nog een translatie in N.

Het nieuwe symbool e en de oude symbolen a, b, c, d, n zullen nu opnieuw worden gedefinieerd in termen van dit nieuwe criterium en van het Bravais-type van net N. Dit net is monoklien of orthogonaal of tetragonaal primitief (mp of op of tp) of orthogonaal gecentreerd (oc). Alleen bij netten van het oc-type N is een Ee-glijvlak mogelijk. Het symbool En geldt voor netten N van het Bravais-type mp of op, terwijl Ed geldt voor netten N van het oc-type. (Zoals vermeld in een voetnoot bij tabel 1.3 in ITA83: “Glijvlakken d komen alleen voor in orthorhombische F-ruimtegroepen, in tetragonale I-ruimtegroepen, en in kubische I- en F-ruimtegroepen. Zij komen altijd voor in paren met alternerende glijvectoren”). In tegenstelling tot de vlakken Ea, Eb, Ec en Ee is er voor de vlakken En en Ed echter geen glijvector evenwijdig aan of loodrecht op een conventionele as in N.

De hieruit voortvloeiende definities van de glijvlakken van de bovengenoemde soorten zijn samengevat in de regels (i) en (ii) van Tabel 3, en meer expliciet in Fig. 3.

Tabel 3. Gedrukte symbolen voor speciale soorten glijvlakken
Aantal glijvectoren evenwijdig aan of loodrecht op kristalassen in net N	Bravais-type van net N
Het symbool wordt bepaald door twee criteria. Het ene criterium is het Bravais-type (mp, op, tp of oc) van het net N gevormd door de symmetrievertalingen evenwijdig aan het beschouwde vlak. Dit net bevat altijd ten minste één conventionele kristalas.* Het andere criterium heeft betrekking op de oriëntatie van de glijvectoren ten opzichte van deze assen.
	m, op, tp	oc
(i) Een of twee parallelle	Ec(Ea, Eb)	Ee
(ii) Geen enkele parallel, geen enkele loodrecht	En	Ed
(iii) Geen enkele parallel, één loodrecht	Ek	–

* Zoals gedefinieerd in ITA83, § 9.1; voor rhombohedrale ruimtegroepen worden hier echter alleen zeshoekige assen gebruikt.

Alle resterende glijvlakken waren voorheen zonder specifiek symbool. Zij hebben elk een diagonale oriëntatie (slechts één conventionele kristalas in het net N). Onder de glijreflecties in hun elementenverzameling is er geen met een glijvector langs die as. Echter, één glijvector staat er (door symmetrie) loodrecht op. Een symbool lijkt wenselijk, dus wordt weer een nieuwe letter voorgesteld: k. Het nieuwe symbool Ek is kort gedefinieerd in regel (iii) van Tabel 3 en wordt volledig geïllustreerd in het onderste blok van Fig. 3. Enkele voorbeelden zijn gegeven in § 2.

Fig. 3. (Bewerking van de tekeningen van W. Fisher.) Alle mogelijke aspecten van de elementensets van glijvlakken weergegeven als in fig. 1, maar onafhankelijk van aslabels. De diagrammen zijn gegroepeerd in kolommen die worden aangevoerd door het Bravais-symbool (bovenste regel) van hun netten N, cf. Tabel 3. De andere criteria van die tabel worden geverifieerd door eerst te kijken naar de dubbele lijnen die de richtingen van de kristalassen in het vlak aangeven. Eén rand (verticaal) van het getoonde net van N is altijd langs zo’n as gekozen. De andere rand is horizontaal, behalve in (1) en (8). Voor de diagrammen (1),,(5) is het glijvlaksymbool het label a, b of c van de verticale as; voor de andere is het de omcirkelde letter in het omlijnde blok dat het diagram bevat. Let op de verticale glijvlakvectoren in de diagrammen (1),,(7), de horizontale in (6), (7), (14), (15) en de afwezigheid van een van beide in (8),,(13). Een voorbeeld van voorkomen wordt onder elk diagram gegeven door het symbool van de ruimtegroep en het coördinatendrietal van het vlak.

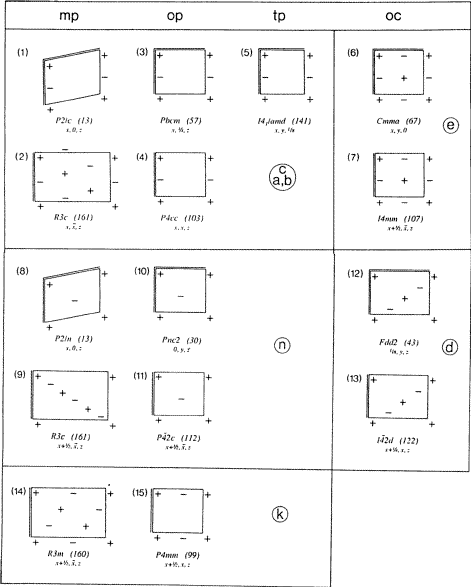
$\begin{figure} \includegraphics {fig3.ps}$

In fig. 3 is Fischers inventaris van alle typen glijvlakken in verkorte – maar nog steeds volledige – vorm weergegeven, waarbij de kristalassen grafisch meer op de voorgrond zijn getreden. Voor elk diagram is een voorbeeld gegeven van het voorkomen ervan in een ruimtegroep.

In sommige rhombohedrale ruimtegroepen komen diagonaal georiënteerde Ec, En en Ek vlakken voor met mp-type netten N die beschreven kunnen worden door drievoudige centrering van een orthogonaal net. Een rechthoekige drievoudige maas van het net N is voor deze typen glijvlakken weergegeven in Fig. 3, diagrammen (2), (9) en (14). In diagram (9) wordt de overeenkomst met andere n-diagrammen zoals (8) of (10) herkend als in (9) een monoklien primitief netwerk van net N wordt beschouwd met diagonale glijvectoren.

Grafische symbolen voor symmetrie-elementen

De bestaande grafische symbolen zoals gedefinieerd en gebruikt in ITA83 worden door het ad hoc comité op één uitzondering na adequaat geacht. De situatie verschilt sterk van die van gedrukte symbolen, omdat in tekeningen de projectierichting een toegevoegde parameter wordt. In de hierna gebruikte termen “loodrechte projectie” en “parallelle projectie” verwijzen loodrecht en evenwijdig naar de oriëntatie van de projectierichting ten opzichte van het glijvlak.

Voor een Ee-vlak bestaat het symbool 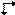voor de loodrechte projectie ervan. De bestaande grafische symbolen voor de parallelle projectie van een Ee-glijvlak hebben echter te lijden onder dezelfde dubbelzinnigheid als de gedrukte symbolen. Zij geven de glijvector evenwijdig aan of loodrecht op de projectierichting weer, maar de keuze is arbitrair. Daarom wordt een nieuw symbool voorgesteld voor de parallelle projectie van een Ee-glijvlak, namelijk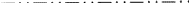

Voorbeelden van Ee-glijvlakken.

Alle glijvlakken evenwijdig aan twee assen in de ruimtegroepen Fmm2, Fmmm, , en $Fm\bar 3c$ (nrs. 42, 69, 202, 225 en 226), alsmede bepaalde vlakken in de vijf ruimtegroepen genoemd in §3.

Diagonaal georiënteerde Ee-vlakken komen voor in de ruimtegroepen I4mm, I4cm, , I4/mmm, I4/mcm, en (nrs. 107, 108, 121, 139, 140, 217 en 229).

In ITA83 zijn al deze Ee-vlakken in hun parallelle projecties tamelijk willekeurig getekend als ofwel gestippelde ofwel gestippelde lijnen. Fig. 4 toont het diagram van ruimtegroep I4cm (nr. 108), zowel zoals weergegeven in ITA83 als met gebruik van het nieuwe symbool.

Fig. 4. (a) Diagram van ruimtegroep I4cm (nr. 108) ontleend aan ITA83. (b) Idem, gewijzigd door gebruikmaking van het in § 2 voorgestelde grafisch symbool, voor de parallelle projectie van een Ee-vlak.

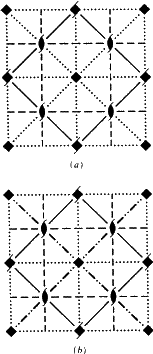
$\begin{figure} \includegraphics {fig4.ps}$

Hoewel Ek een nieuw druksymbool is, zijn in de diagrammen van ITA83 alle glijvlakken Ek op bevredigende wijze getekend met dezelfde conventies als gebruikt voor Ea/b/c glijvlakken. Net als in deze gevallen is er één speciale glijvector (loodrecht op de kristalas in net N, cf. Tabel 3). Wanneer deze vector bijvoorbeeld evenwijdig is aan het projectievlak, wordt het Ek-vlak altijd getekend als de stippellijn die door de desbetreffende conventie wordt voorgeschreven. Daarom wordt geen nieuw grafisch symbool voorgesteld voor Ek glijvlakken.

Voorbeelden van Ek vlakken.

Zulke vlakken zijn gemakkelijk te vinden in de diagrammen van ITA83 als vlakken evenwijdig aan slechts één as en geprojecteerd als stippellijnen, b.v. xxz in P4bm en $P\bar 42_1m$ (nrs. 100 en 113). In het bijzonder is tabel 3 precies in overeenstemming met het getoonde onderscheid tussen vlakken Ek en En. Zie bijvoorbeeld de stippellijnen en de stippellijnen voor R3m en R3c (nrs. 160 en 161).

Hermann-Mauguin ruimte-groep symbolen

De tekens die achter de tralie-letter staan in het Hermann-Mauguin (HM) symbool van een ruimte-groep waren oorspronkelijk bedoeld om voortbrengende operaties van de groep weer te geven. Zo was b een b-glijdende spiegeling in een vlak georiënteerd volgens zijn positie in het HM-symbool.

In de praktijk namen de populaire, zij het slecht gedefinieerde symmetrie-elementen de plaats in van de operaties. Zo werd b gezien als een glijvlak, Eb in onze huidige terminologie. Die herinterpretatie kan geen kwaad, behalve wanneer de bewerking behoort tot een Ee-glijvlak. Als dit geldt, bijvoorbeeld voor de bovenstaande b-glijspiegeling, dan is er wel een Ee maar geen Eb-glijvlak in de overeenkomstige oriëntatie. In dit geval wordt b een zeer misleidend teken. Afgezien hiervan is het vooroordeel (gegeven aan b boven a of c) even storend als in het geval van de symmetrie-element symbolen behandeld in §1.

Daarom wordt voorgesteld zulke misleidende letters a of b te vervangen door e in alle vijf HM symbolen waarin zij voorkomen:

Ruimte groep No.	39	41	64	67	68
Symbool in ITA83:	Abm2	Aba2	Cmca	Cmma	Ccca
Nieuw symbool:	Aem2	Aea2	Cmce	Cmme	Ccce.

Een ander voordeel van de voorgestelde nieuwe symbolen is dat e – in tegenstelling tot a of b – neutraal is en dus niet verandert bij aspermutatie.

Gedrukte symbolen voor symmetriebewerkingen

Een complete set van gedrukte symbolen werd ontworpen door W. Fischer & E. Koch (ITA83, §11.2) en werd uitgebreid toegepast in de secties Symmetriebewerkingen van de ruimte-groepsbeschrijvingen.

In het kort bestaat elk symbool uit maximaal drie delen. Het eerste deel is een enkel karakter (soms met een index) dat het soort operatie beschrijft. Het volgende deel (of de volgende delen) geeft (geven) de componenten van een relevante verschuivings- of vertalingsvector – altijd tussen haakjes – en de coördinaten van het geometrische element van de bewerking, in die volgorde.

De commissie ad hoc wenst na bestudering van dit systeem twee wijzigingen aan te brengen voor glijreflecties:

(i) in plaats van het huidige eerste teken (dat a, b, c, n, d of g kan zijn), steeds de letter g schrijven;

(ii) steeds de componenten van de glijvector (tussen haakjes) voluit schrijven, in het bijzonder voor de eenvoudige glijreflecties in a-, b- of c-glijvlakken waar zij vroeger werden weggelaten.

Regel (i) onderdrukt informatie over het soort glijvlak waartoe de bewerking behoort. Heel vaak is die informatie irrelevant of zelfs verwarrend. Voor a/b/c vlakken kan de onderdrukking essentiële informatie teniet doen, maar het verlies wordt hersteld door regel (ii) zoals in het voorbeeld hieronder.

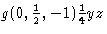Door deze veranderingen aan te nemen wordt de uniformiteit van de symbolen – ook met betrekking tot die voor rotaties – sterk verbeterd. Zo komt het symbool van de glijreflectie in het vlak $x = \frac{1}{4}$ , met de ongebruikelijke glijvector $(0, \frac{1}{2}, -1)$ , namelijk $g(0, \frac{1}{2}, 1) \frac{1}{4}yz$ , nu overeen met dat voor een eenvoudige b-glijreflectie. In ITA83 werd deze laatste aangeduid met $b \frac{1}{4} y z$ , maar dit wordt door regel (ii) veranderd in $g(0, \frac{1}{2}, 0) \frac{1}{4} y z$ .

De bovenstaande regels gelden evenzeer voor glijreflecties die behoren tot de elementenverzameling van een spiegelvlak. Dus, als de verschuivingscomponent van zo’n bewerking (0, 1, 2) is, dan begint zijn symbool met g(0, 1, 2), niet met m(0, 1,2).

International Tables for Crystallography (1983). Vol. A, bewerkt door TH. HAHN, met name §§ 1.1, 1.3, 1.4, 7 en 11. Dordrecht: Kluwer Academic Publishers.

International Tables for Crystallography (1989). Vol. A, 2nd, revised, ed., edited by TH. HAHN. Dordrecht: Kluwer Academic Publishers.

WOLFF, P. M. DE, BELOV, N. V., BERTAUT, E. F., BUERGER, M. J., DONNAY, J. D. H., FISCHER, W., HAHN, TH., KOPTSIK, V. A., MACKAY, A. L., WONDRATSCHEK, H., WILSON, A. J. C. & ABRAHAMS, S. C. (1985). Acta Cryst. A41, 278-280.

WOLFF, P. M. DE, BILLIET, Y., DONNAY, J. D. H., FISCHER, W., GALIULIN, R. B., GLAZER, A. M., SENECHAL, M., SHOEMAKER, D. P., WONDRATSCHEK, H., HAHN, TH., WILSON, A. J. C. & ABRAHAMS, S. C. (1989). Acta Cryst. A45, 494-499.

…vectoren. De glijvlaksymbolen c, n en k voor de drie diagrammen (2), (9) en (14) van fig. 3 zijn uiteraard toegekend volgens tabel 3. Een lid van het ad hoc comité (professor Wondratschek) is van mening dat het symbool n voor diagram (9) in strijd is met de traditionele opvattingen over n-vlakken. Hij stelt voor om aan diagram (9) een speciaal symbool toe te kennen. Dit voorstel heeft echter onvoldoende steun gekregen binnen het Ad-hoc Comité.

Symbolen voor symmetrie-elementen en symmetriebewerkingen